在超声检测中，无论是探测材料表层及内部缺陷，还是对材料组织结构进行表征和应力评价，超声波回波信号都非常重要。一方面，超声波回波信号中携带了大量与被测对象特性有关的丰富信息；另一方面，超声波回波信号会受到仪器、探头、耦合、被测材料等多方面因素的影响，因此，如何最大限度地剔除这些不利因素的影响，获取与被测对象特性有关的有用信息，就成为超声检测技术的关键环节之一。传统的超声检测技术主要基于超声传播时间和回波幅度分析来获得介质特性的有关信息，由于仅仅利用了波形所包含的大量信息中的一小部分，因此不但大大限制了超声检测技术的应用范围，而且导致检测结果可靠性不高，且存在一定的主观性。因此，近年来超声检测信号的处理方法已成为研究热点。

从信号处理分析域角度来看，当前用于超声波信号处理的不单是时域分析，还有频域分析以及时频分析。已经使用和正在研究的信号处理方法主要有空间平均、自适应滤波、Gabor变换和小波分析、频谱分析、裂谱分析等。

空间平均是早期时域信号处理方法，超声检测过程中，通过小幅度随机移动探头（探头移动距离与晶粒尺寸相当），使得来源于仪器电路、模数转换过程等外部检测条件和环境的散射信号产生随机变化，而缺陷信号基本不变，将多次测量的信号相加取平均值，能够有效剔除散射信号的影响，提高信噪比。由于这种检测方法要取多次测量的平均值（次数越多，效果越好），所以效率比较低，而且还会引起信号失真。

自适应滤波^[118]是一种特殊的有限冲击响应Wiener滤波，利用前一时刻获得的滤波结果，自动调节现时刻的滤波器参数，以适应信号和噪声的未知特性，从而实现最优滤波。最优的准则：最小均方误差准则（Minimum Mean Square Error，MMSE），即使误差的均方值最小；最小二乘准则（Least Square Error，LSE），即使误差的平方和最小。实践表明，这种方法无法检测出小缺陷，而且对粗晶材料超声信号处理效果一般。

频谱分析技术是在频率域内揭示及分析信号或系统特性的一种技术方法。自1960年Gericke将基于傅里叶变换原理的频谱分析技术用于探测材料内部的不连续性以来，超声频谱分析在材料的超声检测与评价中获得了广泛应用，不但能够提供有关缺陷取向、表面粗糙度、内含物等用传统的波形分析难以获得的缺陷信息，而且对材料组织结构、性能以及粘结质量等的检测、表征和评价成为可能。因此，基于频谱分析方法的信号处理技术已经成为现代超声检测技术的重要组成部分。国内外很多学者进行了这方面的研究，并取得了许多研究成果。如Gericke O R^[119]采用高阻尼的钛酸钡探头，对含有3.2mm（1/8in）和0.8mm（1/32in）圆柱形孔的铝试样进行了一系列超声波实验，时域波形和频域波形如图1-5所示。可以看出两种试样对应的时域波形几乎相同，但是在5～14MHz范围内进行频谱分析得到的结果却有明显差别，由此可见，频谱分析技术对于区分缺陷尺寸具有重要作用。Anders From和Sandstrom将基于频谱分析技术的现代图像处理方法用于钢种带状组织的无损评价。

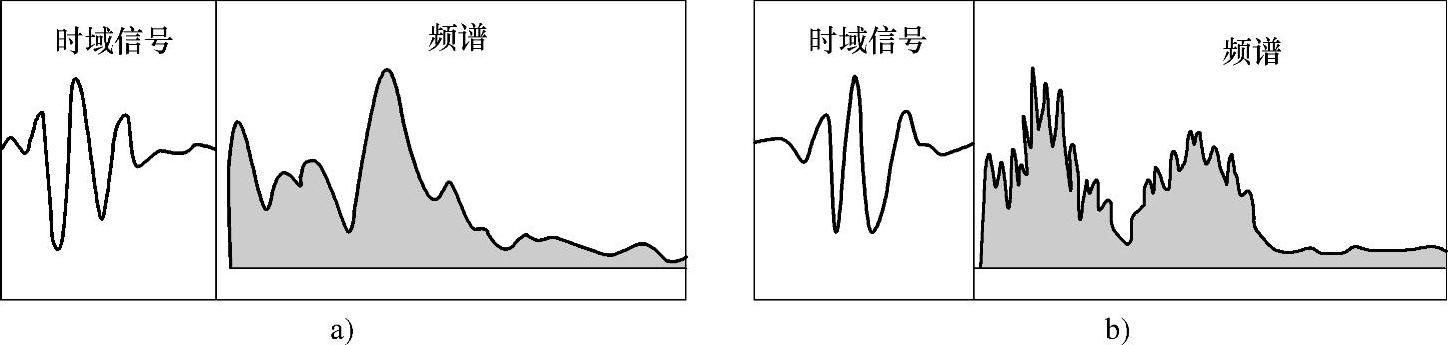
图1-5 铝试样上不同直径圆柱孔的超声波时域信号波形和频谱图

a）3.2mm（1/8in） b）0.8mm（1/32in）(www.daowen.com)

尽管频谱分析技术在超声检测领域已经得到了广泛应用，但现有的商业化仪器或系统仍然采用的是传统的时域信号处理方法，因此，只有将频谱分析信号处理功能以软件或硬件实现，并将其用于商业化仪器和系统设计中，频谱分析技术的研究成果才能更好地推广和普及。

时频分析^[120-121]是局部化信号分析技术的总称，时频分析方法主要包括窗口傅里叶变换（Gabor变换）、小波变换、Wigner-Ville分布、希尔伯特黄变换（Hilbert-Huang Transform，HHT）。时间和频率是描述信号的两个最重要的物理量，时频分析方法提供了时间域与频率域的联合分布信息，清楚地描述了信号频率随时间变化的关系，能够揭示出更丰富的信号内涵。

美国的Malik M A^[122]博士通过对超声信号多种时频分布效果的对比得出小波分析是适合于超声时频表达的最佳时频分析方法。Malik M A博士的研究工作是以最佳的时频分析方法来表达超声信号，1998年，Malik M A提出基于时频集中函数的超声信号窗口傅里叶变换时频表达的参数优化方案，他的工作没有涉及如何从超声时频图像中提取特定信息的方法研究。与傅里叶变换相比，小波变换是时间（空间）频率的局部化分析，它通过伸缩平移运算对信号（函数）逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，因此，小波变换在超声检测领域得到了广泛应用。目前，超声检测领域应用的小波变换分为离散小波变换和连续小波变换，其变换的基本思想都是通过在信号的小波分解系数上作用阈值算子，将大部分噪声及接近噪声强度的小波系数均视为零而舍去，使信号中隐含的能量集中反映在少数几个振幅较大的小波系数上。在此过程中，要做到既去除大部分噪声，又不会引起重建信号的明显失真，关键在于阈值的选择与量化。因此，很多学者提出了多种理论和经验阈值模型，例如Heursure阈值、Minmax阈值、Sqtwolog阈值、Donoho阈值等。2002年，西班牙学者Lazaro J C^[123]等人对3种阈值（Universal，Minmax，Sure）在超声连续小波分析中的应用进行了研究。

超声检测信号中的噪声可分声学噪声和非声学噪声两大类。声学噪声来源于介质内部不同阻抗（如晶粒）界面上的反射、折射和散射，反映的是介质的微观结构。非声学噪声主要包括电子电路噪声、脉冲噪声等，来源于仪器电路、模数转换过程等外部检测条件和环境。两类噪声之间有本质区别，分析和处理方式也不同。非声学噪声是白噪声，与缺陷回波信号不相关，在整个观测时域内服从均值为0的高斯分布，采用小波变换能够实现缺陷信号与非声学噪声的近似最优分离^[124-126]。Karpur P、Shankar P M、Rose J L^[127]等的研究表明，声学噪声在部分时间区间上与缺陷回波信号是相关的，采用常用的信号处理方法（如小波变换、信号平均技术、滤波技术等）去噪效果不是很理想。因此，如何有效去除此类噪声，成为近年来超声检测信号处理的难点和热点。

为了有效去除超声检测信号中的各类噪声（非声学噪声和声学噪声），提高对材料中各类缺陷，尤其是小缺陷的检出率，清华大学的张秀峰博士^[128]提出了基于匹配追踪的超声时频图像信息提取方法并通过对典型粗晶材料的检测实验证明，这种方法能够有效去除超声检测信号中的晶粒散射信号（声学噪声），能达到对0.6mm晶粒平均直径的粗奥氏体不锈钢中0.8mm平底孔和0.5mm横孔的超声检出能力。同济大学声学研究所的刘镇清^[129]等人采用维格纳（Wigner）变换提取信号的特征，结合人工神经网络识别超声检测信号，并通过实验验证了该方法的有效性。西安交通大学的陈岳军、史耀武^[130]采用小波变换模极大值方法提高信噪比，利用此算法对粗晶奥氏体不锈钢的超声检测信号进行分析，效果良好。

综合上述超声信号的时频分析方法可知，目前，提取超声检测信号中有用信息的方法主要有两种：模式识别和降低噪声（增强缺陷回波）。模式识别一般要结合人工神经网络技术，该方法的准确性和可靠性取决于预先检测信号的样本数，因此局限性显而易见；降低噪声一般采用小波变换方法，但目前小波函数的理论水平有待进一步提高，例如目前对小波基的选取还没有严格的准则和适宜的方法，而不同小波基的选取会对超声信号分析结果产生很大的影响。因此，如何解决上述问题，需要今后进一步探索和分析。