相对于带有更多突发性过渡的语音网络，无线数据网的构建往往基于在良好和不良状态之间的温和过渡（见参考文献［RaJo05］）。这一平滑的过渡方程代表了用户无线接入的效用，或我们在将来所说的有效性。这一部分会尽最大的努力服务于网络用户，因为众所周知，用户必须接受它所获得的服务质量，因此不会明显地存在单一性能指标。

考虑的第一种有效性指标是吞吐量，参考文献［Radi01］，［Radi02］和［RaJo05］均研究了H2网络吞吐量。第二种方法是能量效率和相应的最优化方案，如参考文献［RaJo03］所述。参考文献［RaJo04］给出了这两种方案的额外研究结果。

实例H2系统是一个集中化系统，其中接入点（AP）负责管理所有资源。在集中化模式中的通信仅发生在AP和移动台（MT）之间。在每次连接中移动台根据它们的缓冲状态在上行链路中请求一个发射机会。而AP根据自己本身的缓冲状态在下行链路中分配发射机会。H2的标准支持LA，例如，在物理层使用不同的初始发射速率的能力（也称为PHY模式，PM），其中，高速率适用于良好的信道状态而低速率适用于不良信道状态。它也支持TPC，其中，AP广播它的发射功率P_t，AP和它的期望接收功率P_e，AP。这样，MT可以通过接收到的信号计算路径损耗PLOS，并调整它的发射功率使得AP处的接收功率P_r，AP等于P_e，AP。有关H2和它的LA、TPC方案以及调度算法在所有研究的更多的信息在参考文献［Radi04］、［RaJo05］和［KMST00］中给出。

所有的研究都是基于参考文献［KJMST00］中的PER曲线。根据ARQ协议和每PM中的原始数据速率R_PM，（1-PER）可以解释为帧成功率，而自动请求重发（ARQ）以后的吞吐量为T_PM=R_PM·（1-PER）。以R_PM为参量的吞吐量曲线如图8.17所示。需要注意的是，在给定一个信干噪比（SINR）数值的情况下，经常存在一个带有最大吞吐量的PHY模式。这一成果可以在将来用于吞吐量的研究中。

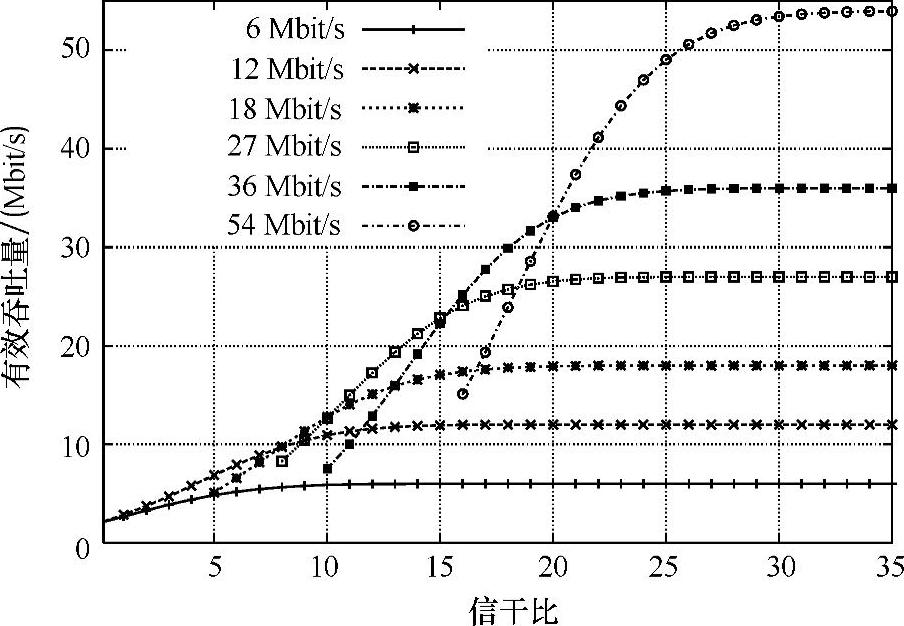
图8.17 以R_PM为参量的理论可以达到的有效吞吐量

在蜂窝网中，小区内的干扰是不可避免的。给定LA和TPC的法则，H2系统中的接入点就可以通过增加发射功率，允许高数据传输速率的使用来增加其小区内的数据吞吐量。但是，这一方法也会增加其他小区的小区内干扰，反过来说，这样可能会促使其他小区增加发射功率来提高它们的负载干扰比（C/I）。考虑到不同干扰类型的H2无线电干扰的一些基础性能在参考文献［Radi01］中被分析。基于文献中H2系统的PER曲线形成过程，研究了在短期内利用高功率发射相同数量的数据还是利用最低可能发射功率慢慢发射数据的问题。研究结果表明，考虑到干扰小区内自动请求重发后的数据吞吐量，利用越低的发射功率发射时间越长越好。

这一初始化结果被参考文献［Radi02］采用。H2是基于同等时间间隔下的MAC帧。所以如果发射速率高于所需速率，就会有备用资源，这些备用资源由超过某个大小的MAC帧中未使用的部分表示。根据参考文献［Radi01］中的结果，将发射功率降低到最小是可取的。图8.17中吞吐量随着SINR单调递增，并且假设干扰连续，SINR与发射功率成正比。因此，为了将发射功率降至最小，参考文献［Radi02］中提出了一种算法，分析了MAC帧中未使用的部分，并且逐渐降低发射功率，直到未使用的部分变得足够小。如果未使用的部分非常小而缓冲状态增加，发射功率也会随之增加，直到缓冲状态足够短且未使用部分仍然很小。

经研究，这一方案的实现结果令人满意，除非系统中有很高的负载。但是该方案并没有考虑小区内干扰，因为方案中假设吞吐量随着发射功率单调递增，如图8.17所示，这种情况仅适合于连续干扰。如果相邻无线小区也调整它们的干扰，这一假设就不复存在。因此，所有的后续研究仅建立于一个简单的蜂窝网场景下。

本节中的一个有趣的问题是，最大的网络吞吐量是否是在最大的发射功率条件下达到的呢？参考文献［RaJo05］中设计了一个模型来回答这一问题。针对这一目的，为蜂窝H2网络设计了两个模型:

1）用于计算基于H2的常规蜂窝网吞吐量的话务流量模型。这一模型考虑了所提的调度算法并利用TPC参数的固定值，例如P_t，AP和P_e，AP。它仅仅考虑了取决于接收端SINR的线路放大器（LA）。这一模型从几何角度来说是基于对接收端SINR的PDF的计算，并利用图8.17的吞吐量曲线来计算吞吐量的预期值。该文章分别提出了单一无线小区、两干扰小区和常规网络的模型。(www.daowen.com)

2）H2的仿真模型，其中包括物理模型、MAC和ARQ协议、汇聚层以及与解析模型中相同的调度算法实现。移动台在在一个圆形区域移动，相当于在接入点周围分布，生成的数据包在AP和MTs之间双向传输。

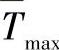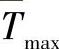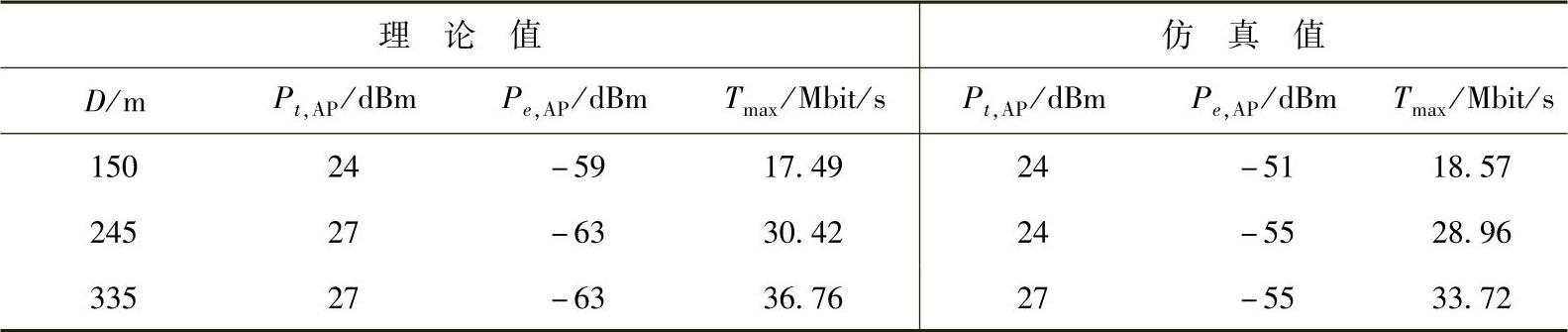
解析模型是为高负载情况设计的，仿真模型中的参数已做出相应的调整。两个模型中得到的结果吻合得很好，这表明，所给出的调度算法中，网络吞吐量的最大值不是在最大发射功率处达到的。这意味着从吞吐量的观点来看降低发射功率可能是有用的。对于考虑的情况来说，P_t，AP的影响比P_e，AP更为明显一些。参考文献［Radi04］中的其他结果显示，对于最大平均吞吐量来说，P_t，AP的理想值在无线小区之间的距离D和小区半径R之间的比例恒定的条件下是不变的。在两个模型中，当R=50m，D为不同值时，为达到而从最优解P_t，AP，opt和P_e，AP，opt中选择的结果在表8.13中列出。

表8.13 针对两个模型在T_max下结合P_t，AP，opt和Pe，AP，opt

我们同时提出了另一种方法，可以同时控制LA和TPC。它取决于如有效性以及可以在能量的每个单元发射的比特数等的能量效率。这对于电源驱动移动台的上行链路发射非常重要。参考文献［RaJo03］中提出了一种基于LA和TPC的博弈论模型来增加能源效率ξ的算法。PHY模式（PM）下一个单一发射-接收对i的有效性被定义为

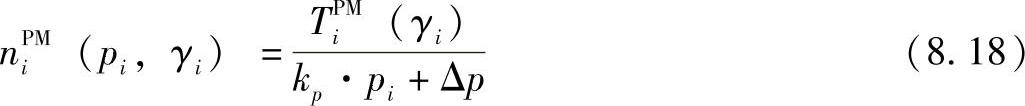
从图8.17中可以看出，它主要取决于发射功率p_i以及在接收端γ_i和T^P_iM（γ_i）情况下的信干噪比γ。参数Δp避免了解决方案在p_i→0时导致的有效性趋于无穷的情况。k_p的引入增加了一些算法灵活性。需要注意的是由于参数Δp和k_p的引入，效用函数不等于ξ的物理定义，而是等于ξ的一个测量值。图8.18显示了不同PM下的各种效用函数n^P_iM实例。

遗憾的是，博弈论不能通过解析进行分析，因为它的效用函数并非连续可微。对一个相似的虚拟博弈论和该博弈论的收敛性进行分析，显示可以达到一个平衡。参考文献［RaJo03］中提出利用与上述吞吐量结果相同的仿真模型对博弈论的结果进行定量计算。将所得出的吞吐量和ξ结果与最大吞吐量结果进行对比，并在表8.13中列出。本节中的主要结论是ξ的增长经常意味着吞吐量的下降，因此，通过对该博弈论效用函数参数的改变，可以权衡ξ和吞吐量。

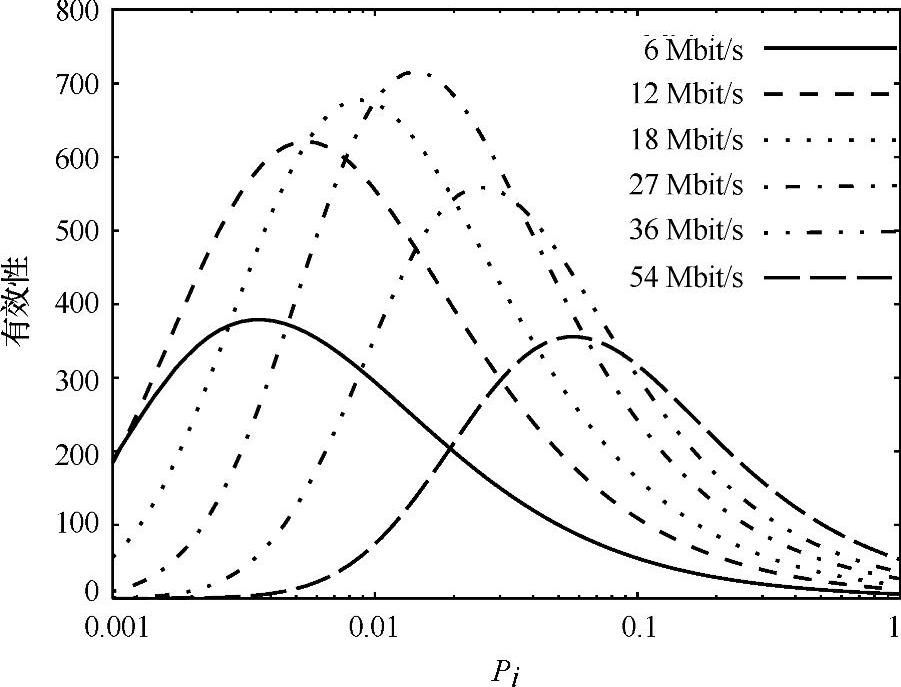
图8.18 效用函数n^P_iM