1.在热点中通信基站的数量

参考文献［OrBa03a］利用上述分析来解释在半径为r到r+δr之间的圆环内，与移动台之间夹角为2θ（r）的通信基站数分布为均值如下的泊松分布:

μ_r，r+δr;θ=θ（r）ρ［Ψ（a，b₁，b₂，c;r+δr）-Ψ（a，b₁，b₂，c;r）］0≤θ≤π （8.9）

式（8.9）也可以写作

这一结果让我们考虑到一个指定区域，其中基站的密度在保持不变的情况下，不同于上述平面的其他区域。前一种密度可能会大一些（因为运营商在同一个区域响应递增的移动台传输量），于是这一区域被称为热点。因此，如果一个热点位于半径r₁和r₂的圆环中，其边界是半径为r的圆，用θ（r）表示（其中，对于一个凸区域来说，仅需边界可以用极坐标表示，因此2θ（r）是半径r上两个边界点之间的角距离），这样，热点内的通信基站数为均值如下的泊松分布:

因为Ψ（a，b₁，b₂，c;r）为2rF（a，b₁，b₂，c;r）的不定积分，则有

这些方法可以应用于双斜率模型的情况（该情况中，衰减定律中的功率在某些指定距离内有所改变）。

2.属于一个基站的移动台数目

假设移动台和基站都随机均匀分布在（无限的）平面上，但是有不同的密度，ρ_M和ρ_B。可以与给定移动台进行通信的基站数为一个均值为_μB的泊松分布，而相同地，可以与给定基站进行通信的移动台数量为均值为_μM的泊松分布。这些也可以在之前所述的任何一个损耗模型包括双斜率模型和带热点的模型中发现。在参考文献［OrBa02a］和［VOZB02］中指出，一个给定基站可以从给定移动台接收到最强信号基站的几率为1-e^-μB/μ_B。这样，我们认为移动台属于这一基站。定义最后的概率为p，这样可以看出，可以与给定基站，并且该基站为从其接收到最强信号的基站，进行通信的移动台数为均值为_μMp的泊松分布。因为μ_M是可以与基站进行通信的移动台数的平均值，而p是基站为从与其进行通信的移动台中接收到最强信号的基站的概率，这是意料之中的结果。

这一结果应用于参考文献［OrZB02］和［VOZB02］中来估计一个被带有给定硬盘容量基站的网络服务的用户的阻塞率，换句话说，即可以被一个基站服务的用户数量的最大值。将接入一个基站建模成一个Engsett损耗系统，然后可以用Engsett公式来导出阻塞率。文中为蓝牙散射系统提供的数字结果和图表。

3.在活动设置窗口中的基站数(www.daowen.com)

这里，将移动台的活动设置定义为基站的设置，其中，可以与移动台进行通信的基站有额外的要求，即，接收到的信号强度在一个指定范围内（比如udB）为可接收到信号强度的最大值。这一范围被称为大小为u的活动设置窗口。利用带有对数-正态阴影的单斜率模型，通信基站的平均数为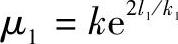，其中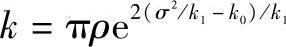，。令为在一个大小为u的活跃设置窗口中至少有m个基站的可能性。这构成了如下递推关系:

其中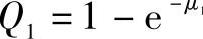，定义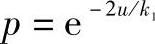，则窗口中刚好有m个基站的可能性为

P_m=Q_m-Q_m+1 （8.14）

式（8.14）等于

pQ_m+（1-p）m_μ^m₁e^-μ1 （8.15）

其中，m≥1。

因此这一概率仅仅取决于p和_μ1。

特别地，当m=1时

当μ₁很大时，这一结果仅仅取决于p，而因为μ₁为通信基站的平均数，这一结果很可能包含了具有实际用途的情况。

在参考文献［MOBB04］中发展了这一理论结果，其中将这一基于理论分析的统计与基于确定性模型的仿真结果进行对比，并找出了相当多的共同点。