在这一节，假设移动台和基站随机均匀地分布在（无限）平面上，但是密度分别为ρ_M和ρ_B。更准确地说，一个节点在一块区域δA中的可能性为ρδA（ρ在适当的情况下等于ρ_M或ρ_B），δA为一阶量，而多于一个节点情况下的可能性则比δA高阶。参考文献［OrBa02b］和［OrBa03b］中列出了大多数情况下用分贝表示的距移动台的距离R（随机）而造成的功率损失，即

L=k₀+k₁lnR+S+T （8.1）

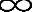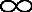其中，k₀和k₁是常数，S是阴影影响，为均值为0方差为σ²的正态分布。T=k₂ln（c+Z₁）2+Z²₂/c²+2，其中Z₁和Z₂为均值为0方差为1的正态独立分布的随机变量，且c≥0（事实上在所有情况下有k₂=10/ln 10，但是对于一个一般数值也是可以进行分析的）。引入常数c来简化标记，莱斯因子K等于10 lg（c/2）。瑞利衰落相当于K=-（c=0）;当K=（c=）时，根本没有衰减。K的有限值（c为有限正值）会造成莱斯衰落。对数-正态阴影相当于σ＞0，当σ=0时没有阴影衰落。对于没有阴影衰落（σ=0）没有衰落（K=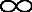）的特殊情况被认为是确定性情况，而没有阴影衰落（σ=0）有瑞利衰落（K=-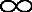）的特殊情况被看作瑞利情况，而没有阴影衰落（σ=0）有莱斯衰落（K无限）的特殊情况被看作莱斯情况。联合阴影衰落（σ＞0）和瑞利衰落（K=-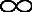）的情况被看作Suzuki分布。联合阴影衰落（σ＞0）和莱斯衰落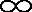（-＜K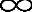＜）的情况是普遍情况，而其他均为特殊情况。

合理选择k₁，算法可以容纳功率和距离之间的逆空间法则，或逆第四功率定理，或任何其他有名的功率定理，而这种在一些特殊距离中可以将一个功率与另一个功率进行转换的算法通过位于或超越该距离时k₁的不同值来确定。值得注意的是，为了简化数学分析，公式中使用自然对数底而不是以10为底的对数。

COST 259会议中许多文献都考虑到了特殊情况T=0（或c=）。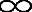

1.互相关通信节点之间的距离

移动台M和基站B在通信范围内的条件是从M到B的损耗不能超过一些特殊值l₁，例如L≤l₁。从这里得到R，S，Z₁和Z₂的联合密度函数为

其中

或者等价于

0≤r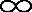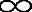＜，-＜z₁，z₂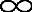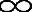＜，-＜s≤l₁-k₀-k₁lnr-t

用于推导的过程与在特殊情况下已经使用的推导过程相同，即在给出其他变量（在一个有限的圆内均匀分布）的情况下获得R的条件分布，然后利用其他变量的已知密度函数重新建立联合密度函数。

经过一些代数运算，得出R的密度函数

其中0≤r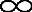＜，且，。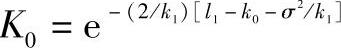

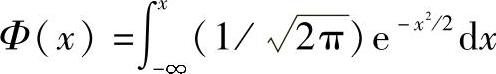
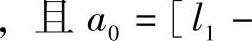
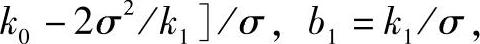
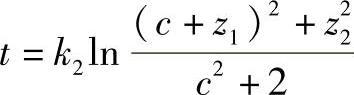这是基站和移动台可以互相通信的距离的密度函数，不考虑阴影衰落的影响。有许多种特殊情况:(www.daowen.com)

1）莱斯情况在没有对数-正态分布阴影的情况下提出，因此S=0。如此，R的密度函数为

2）Suzuki情况，即c=0。这种情况下，积分即可以通过定义U=（Z²₁+Z²₂）/2而简化，则

其中0≤r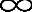＜，且有b₂=k₂/σ，参考文献［OrBa02b］中早已直接给出结果。

3）在特殊情况σ=0时，即瑞利情况下，密度函数变为

其中0≤r＜。

2.通信节点个数

与COST 259会议中文献不同的是，可以接受给定移动台的基站数目的概率分布是可以获得的，方法是在一个移动台周围半径为r且损耗控制在l₁以内的n个基站定义一个概率的生成函数，并求解由此产生的偏微分方程。定义

令P（S+T≤l₁-k₀-k₁lnr），则有

式（8.7）将被定义为Ψ（a，b₁，b₂，c;r），为2rF（a，b₁，b₂，c;r）的不定积分。因此，满足上述约束条件的通信基站的数量为均值为πρ［Ψ（a，b₁，b₂，c;r）-Ψ（a，b₁，b₂，c;0）］的泊松分布。

当r趋近于正无穷时，Ψ（a，b₁，b₂，c;r）的极限为0，因此，损耗控制在l₁以内的基站总数为均值如下的泊松分布:-πρΨ（a，b₁，b₂，c;0）。

在Suzuki情况（c=0）中，令2k₂/k₁＜1，则上式等于

需要指出的是，在k₂=0的情况下，当仅有对数-正态衰落存在，这一结果与已得到的特殊情况下的结果相符。并且这一结果也不能用于逆空间法则，因为在这种情况下，当2k₂/k₁=1时，所需等式不能成立。