明显地，线性基带传播模型使用复杂的数字来代替信号和脉冲响应。不幸地是，一些空时编码技术例如正交STBC（见参考文献［Alam98］、［TaJC99］、［LaSt03］），或许不包括在这些模型中，因为复杂的结合操作可能不能被描述成线性变化的。最普遍地，这个问题通过引入两个线性变化矩阵来解决，一个用于符号，另一个用于符号的复杂信号组合（见参考文献［HaHo02］）。然而，使用这种方法，和输入信号相比，模型不是线性的，并且线性传播模型的一些方便的特性也会丢失。一个不同的方法使用了实值传递矩阵（见参考文献［PSTL03］），这个矩阵基于总的实值矩阵的描述（见参考文献［NeMa93］）。麻烦的是，许多已知的STBC可能被理解成传播的标准格式，那就是说，STBC的编码和解码通过一个简单的矩阵乘法来执行。虽然实值的标记在和正交STBC联合之前就使用了，例如参考文献［StGa03］、［WaTS01］，这些模型都没有提供输入符号通过向量矩阵乘法到输出符号的传递矩阵。

一系列的TD，处理了传递矩阵的不同方面，这些矩阵基于实值标记。把一个复杂的矩阵转化成与它对等的矩阵的规则是

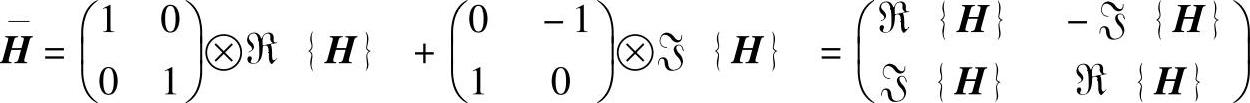
代表Kronecker积。现在传输模型被定义为

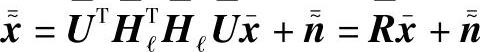
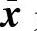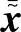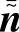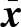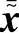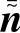式中，是发射符号向量;是匹配滤波后的接收符号向量;是有色噪声（由匹配滤波器U^TH^T_ℓ引起）向量。、和都是由接收向量的实部和虚部得到的实值。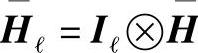，Iℓ是ℓ的单位矩阵。这样，在单抽头MIMO信道中，H_ℓ表示ℓ个时间码片。U—表示扩展矩阵，它能够实现发射端信号星座的线性传递。由于实值标记，传输过程比复数矩阵的传输更加通用。

矩阵的积被写成一个矩阵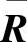。这样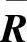，描述了整个过程。

实值传输模型的容量分析和复数模型中一样简单，只不过多了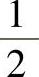

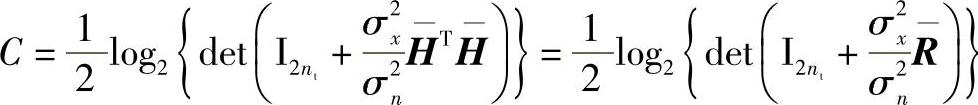
我们假设发射端没有任何信道状态信息。还要注意，我们使用H^TH代替了通常使用的HH^T。这样容量就是传递矩阵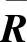的函数。由这些，很快就清楚了任何的扩展矩阵都有可能保护容量。

TD（见参考文献［LiPi04］）以Alamouti为例给出了如何把正交STBC变为线性扩展矩阵，也就是说，我们可能会发现扩展矩阵，它携带了符号间、发射天线间和时间片之间的近似映射。这个模型可能很容易地提供达到正交STBC特性的途径。例如，从扩展矩阵的结构中，不能在任意的信道达到容量要求，因为扩展矩阵有正交列，但是没有自乘。因此，容量可能只在几种信道十分稀疏的情况中能达到（见参考文献［PiLi05a］）。在接收端使用一个天线的Alamouti结构就是这种情况。(www.daowen.com)

基于这些考虑，新的STBC在TD中被提出来了（见参考文献［PiLi05a］）。扩展矩阵取决于正交STBC的分层传输。基于Alamouti结构的扩展矩阵，例如

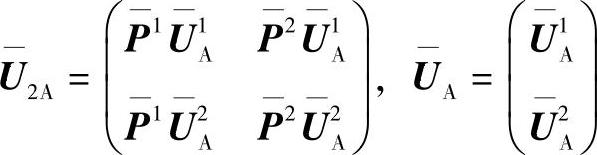
式中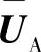，是Alamouti的扩展矩阵;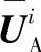是次级展开矩阵，它利用了第i个时间片段的映射。

矩阵P^j对于每一层都不同，并且为了使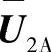成为单一矩阵而选择。在使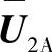成为单一矩阵的设置中，我们可能会选择优化接收到的星座（假设MIMO瑞利信道）距离的设置。图7.10比较了文献中提到过的编码的距离。

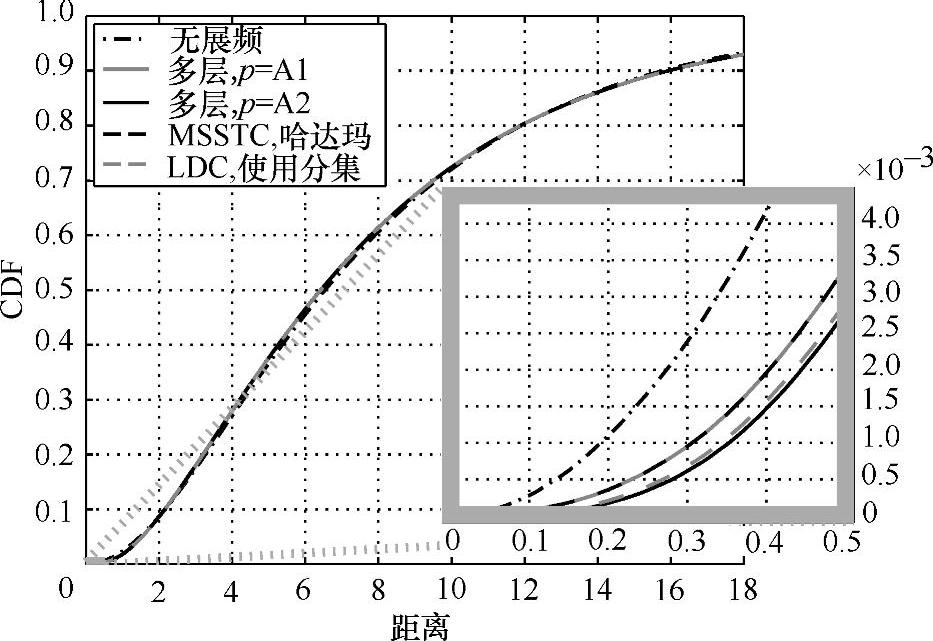
图7.10 各种全速率扩展矩阵（l=2）距离曲线;模型基于4PSK，两发射两接收天线的MIMO瑞利信道，LDC来自于参考文献［HaHo02］，MSSTC来自于参考文献［WaTS01］;此外，矩阵P—^j对于提出的架构的编码有了两种不同的选择

TD（见参考文献［PiLi05b］）进行了不完美信道信息如何对正交STBC性能影响的分析。虽然实值标记可能并不必须，但是它使简单分析成为了可能。考虑到接收符号由两个独立的非中心卡方分布向量的积得到，我们得到了一个准确的结果。另一方面，假设全部干扰和噪声都为高斯分布，基于这点，有了一个近似。天线数量较大时，由于中心极限理论，这个假设也是合理的。图7.11给出了1根、2根、4根天线的分析结果。正如我们看到的，对于4根发射天线，近似值已经相当好了。

实值标记的另一方面是不合适的随机变量可能会出现在传输模型中。一些干扰可能会使一些接收机噪声和干扰不合适。TD（见参考文献［PSTL03］）考虑了这些，并比较了不同的检测技术。由于许多传输技术，例如CDMA、MC-CDMA和MIMO全都可能由传递矩阵表示，让大部分检测技术适应这些结构很容易。

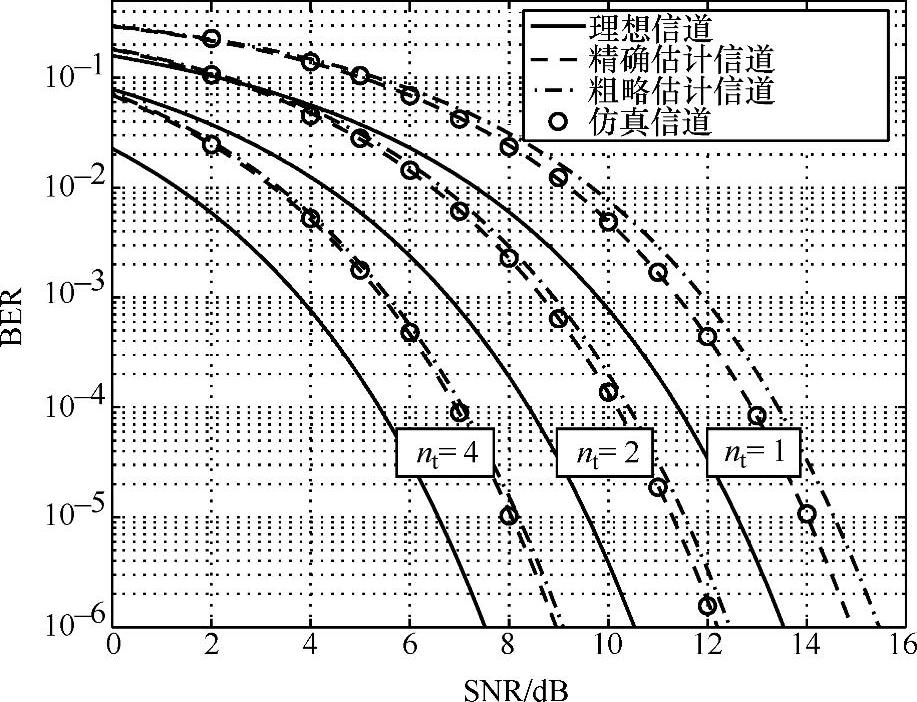
图7.11 4天线接收机BER性能，发射机为2天线和4天线，使用Alamouti码（见参考文献［Alam98］），3/4速率STBC（见参考文献［HaHo02］）