当无线通信系统在发射端和接收端有天线阵列时，上面提到的波束成形的方法可以被用来提高系统吞吐量。特别地，假设在发射端和接收终端获得了信道响应矩阵H的信息，并用它生成了正交空间滤波器。信号带宽假设远小于信道带宽，对于频率选择性信道，特征波束成形和OFDM联合使用形成了多窄带并行系统（见参考文献［Will03］，［Will05b］）。

H的分解为

H=UΣV^H （7.25）

，，Σ的对角线元素为σ_i，i=1，…，σ_N。因此，有非零增益的H至少有N=min（N_t，N_r）个正交模式。

现在等价的系统模型为

X和W是N_t×N和N_r×N的发射机和接收机的空间滤波器矩阵，P=diag（p₁，…，p_N）是功率权重矩阵。权重矩阵通过下式选择:

W=U和X=V （7.27）

式（7.26）则可以写为

因此，发射端的空间滤波器X控制信道的正交特征模式上N个数据子流的方向，使得它可以使用H左奇异向量作为行列式权值而不考虑接收端的干扰就能被获得。特征模式k的信道增益为λ_k=σ²_k，λ_k是H^HH的第k个特征值。

有效的使用特征波束成形的一个重要问题是在每个特征模式上适应性调制和编码方式的选择，功率分布P也很重要。解决问题的方法取决于是否假设了发射端和接收端得到了完整的信道信息或者是只有一个估计H。

1.完美信道信息

基于误码率和中断容量的特征模式下，解决适应功率分配和调制/编码速率的方案被提出。

2.基于误码率的自适应性

在能达到规定误码率性能的结构中，每一个特征模式的功率级和调制星座被选择用来达到最优功率分布上的目标性能。

参考文献［SaTA04］中，确定了BPSK、QPSK和16-QAM在每10个功率级上的BER。提出的功率和调制自适应算法在可能的功率候选值和星座尺寸的设置中搜索以找到最大化总吞吐量的设置。

对于MIMO OFDM，参考文献［MuDa04］中使用了在每个频率载波下的最强的特征模式。为判定星座尺寸，功率载入算法被提出，并在IEEE 802.11a的物理层环境中仿真。在BER为10^-6时，和SISO相比，在2×2MIMO中，提出的适应性功率载入模型提供了超过4dB的增益，和注水法相比近似为1dB增益。

3.基于中断容量的自适应性(www.daowen.com)

参考文献［Fise04］中提出了第一个基于中断容量的自适应策略;在这种方法中，功率分布不连续，目的是最小化中断容量，这等于是最大化相同信息。优化的问题被定义为拉格朗日最小化，这种方法使用迭代局部离散一阶查找方法得到解。功率级L=2，…，6，N_t=N_r=3时，使用迭代方法得到的结果显示，即使较差的功率解决方案也能达到低的损耗概率，同时SNR减小时，小的L值带来的恶化也会减小。

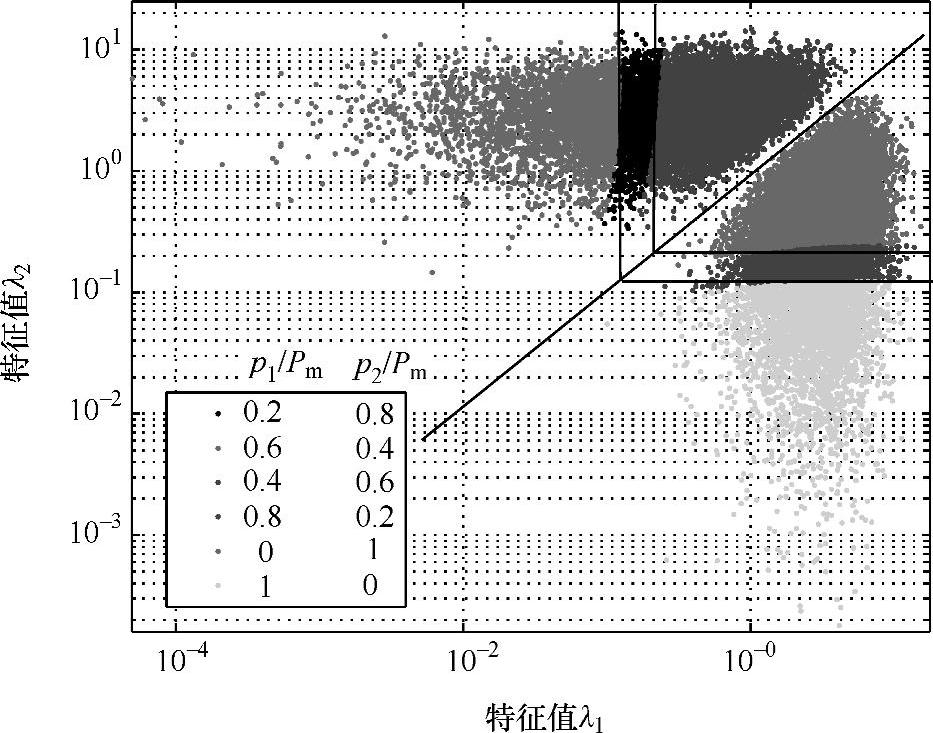
图7.5 迭代法得到的解（N_t=N_r=2，L=6，SNR=10）

这种方法的缺点是每一个连在一起的区间都需要迭代的解。参考文献［Fise04］中提出了一种非迭代的近似解方案，其利用了使用迭代解法时的观测值。图7.5给出了N_t=N_r=2，L=6的2维特征值空间的解的分布。灰色阴影区为不同的可行解。区域被分块，并且是被和坐标轴平行的线分开。预定的界限的使用能快速选择P，其使用了特征值比率。

另一种基于损耗概率自适应功率分布的方法在参考文献［KnSy04b］中提到。在这种情况下，其目的是得到每个特征模式的恒定的目标容量，以及使用最小发射损耗概率的恒定的全部容量。这个标准使所用特征模式的单一码表的使用成为可能。这个问题的一个解决方法是“截断信道水逆”，在这种模式里增益比一些关断的阈值小;然而，损耗概率会变得非零点。参考文献［KnSy04b］中提到的可选的方法是“子空间信道求逆”，这种方法中最差的特征模式一直关闭，N-1维子空间在没有截断的情况下完全反转。

图7.6中给出了使用全空间截断求逆和子空间求逆的未分级的特征模式的遍历容量，同时，获得了在空间和时间上使用优化注水法的遍历容量。注意到信道维度N=min（N_t，N_r）增加时，全空间截断和子空间求逆的差距会减小。

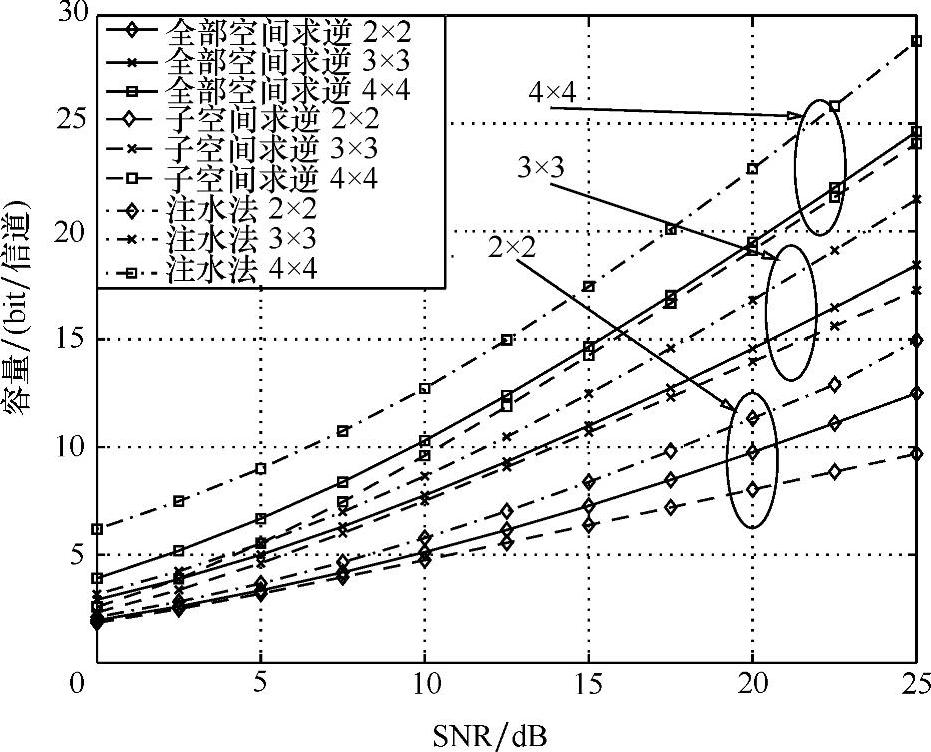
图7.6 未分级的特征模式的遍历容量（使用全部空间截断反演、子空间求逆和注水法）

4.不完美的信道信息

参考文献［SaTA04］中发现，提出的功率和调制自适应算法的性能在仿真和实验间存在差别。注意，为了支持自适应功率的载入，需要信道估计、反馈和同步技术有比较高的精确性。信道估计错误的影响是发射和接收权重行列式（7.27）和信道不匹配，结果导致SI（见参考文献［Will05a］）。信道估计错误引起的SI的影响可以通过干扰分析来估计（见参考文献［Will05a］），并且考虑估计误差影响每一个特征模式的预期的SINR都可以判断出来。这被应用在强加载原理中来选择特征模式的数目，这些特征模式应该能支持需要的性能的传播，并能够有根据地分配发射端功率。通过多种实现方法获得的8×8信道H，分布为CN（0，σ²_n），估计误差σ²_e的SINR，在图7.7a给出了结果。确定的SINR模式1～3为20dB，模式4～6为10dB，模式7和8为5dB。相同模型的来自于注水法分布的SINR结果在图7.7b中给出。强功率载入理论在少于13％的情况中选择了7种或者更多的模式，而注水法方法在超过72％的实现中使用了所有N_t=8模式。

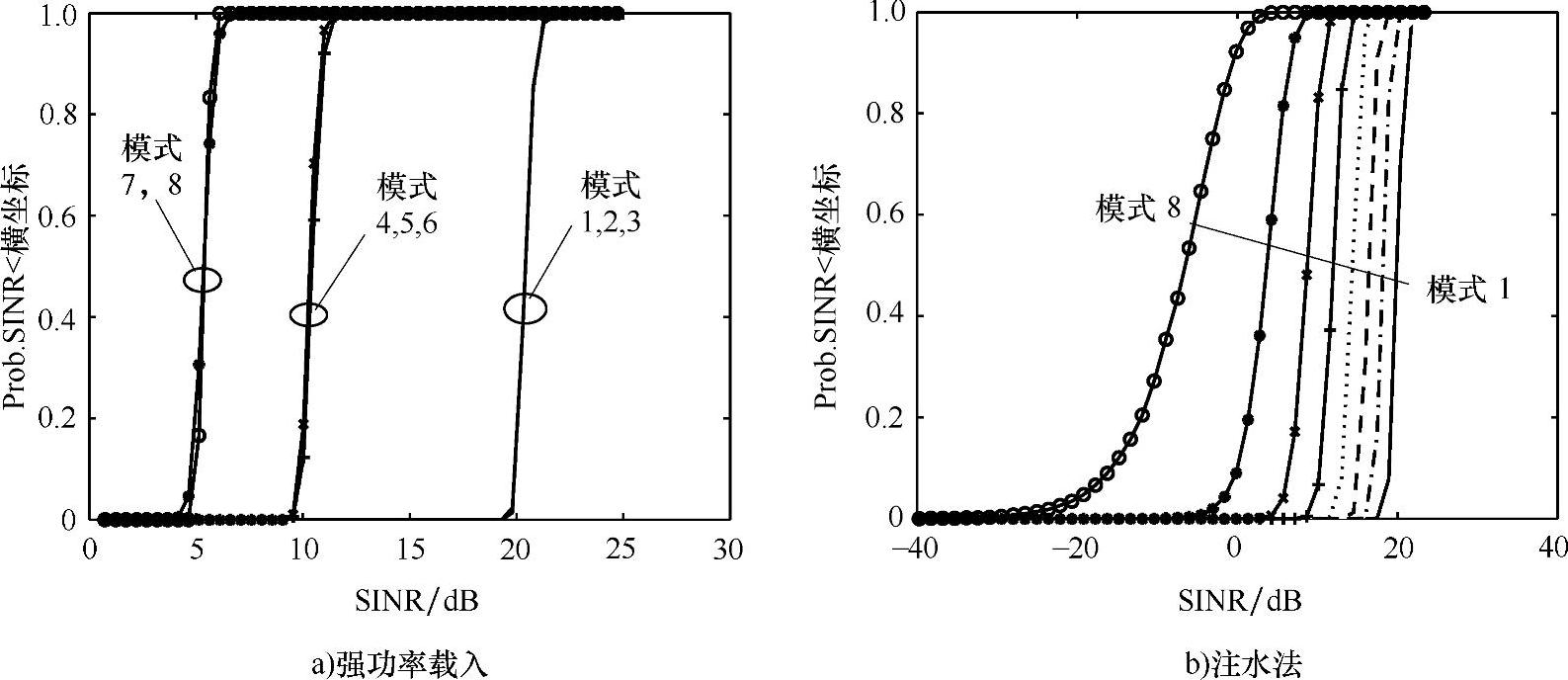
图7.7 不同模式和功率分布算法下特征模式达到的SINR

5.稀疏传播环境中特征波束成形

虽然MIMO系统的研究重点为分散传播环境中应用，但是如参考文献［Will03］、［Will05b］中提到的，混合无线接收系统中特征波束成形和OFDM可以联合使用，这种情况下的稀疏传播环境中MIMO也能得到有用的增益。在加拿大多伦多大概距地面60m，发射端和接收端之间的LoS被小的建筑群分块，在5.75GHz下，通过N_t=N_r=8的ULA得到了信道数据。信道相关的静态特性支持一种特征波束成形技术的使用。信道估计误差导致的自身干扰能够通过限制使用的特征模式的数量来控制。总的来说，在一个使用单元无线的系统中，得到了频谱效率增加的因素。3个元素中的一个增长被认为和使用单数天线元的系统有关。

参考文献［BuHe03］进行了冲击多径和单数向量关系的分析。在两个传播向量分别为h₁和h₂的相互关联的冲击波形中，存在两种极限情况:h₁和h₂正交，U中的单数向量与这两个传播向量一致并且单数的值就是它们两个的标准值。如果h₁^Hh₂≠0并且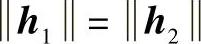，那么单数向量包含两个状态相反的传播向量。因此，单数的向量为“和与差”的形式。当h₁^Hh₂≠0并且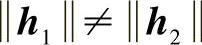，单数的向量在这两种极限情况中，各自的传播向量在各自的单数行列式中，但是有不同的幅度。这种影响会在被测量的数据中发现，正如图7.8所示（见参考文献［BuHe03］）。在AoA为-55°和20°时，最强的两种模式波束同向，预示了一种强的“和”关系。这些影响在参考文献［Will05b］中也有提到，认为在稀疏传播环境中，特征结构高度依赖于频率，因为波长元素分离的比例影响到达的有效角度。

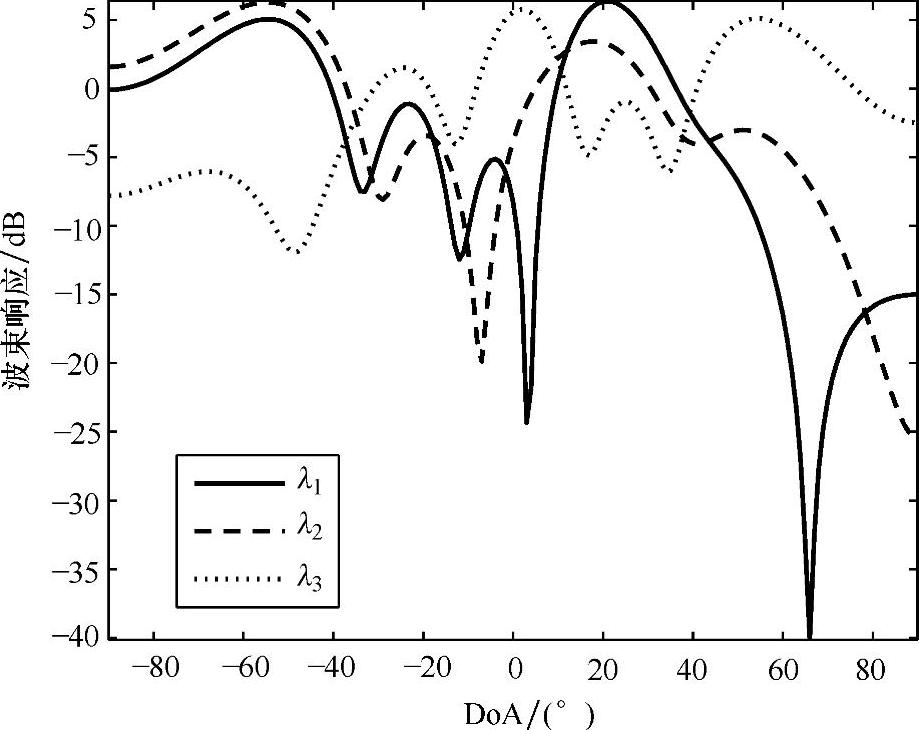
图7.8 多天线测量的3种最强模式的特征波束响应