在每个天线阵列元中，接收机的处理阵列对到达信号进行了复杂的加权处理。加权向量w可以被称为空间滤波器，会导致判定变化。

参考文献［PNTL02］针对最大化SINR优化的空间滤波器被用于宽带信号和各向异性干扰，例如相邻蜂窝用户引起的信号。它包含一个预处理白滤波器来白化有色干扰信号，和一个匹配于发射滤波器物理信道和预处理白滤波器的串联。有色干扰的影响会增加总接收滤波器响应，导致额外的ISI。我们注意到，除非需要的信号和干扰信号有相同的AoA，否则不能估计ISI，即使使用了ML检测;然而，即使在带宽上没有限制，在热噪声存在的情况下ISI的增益总会存在;因此，增加SINR需要全部排除ISI。

参考文献［DuOH05］使用MEA的自适应编码调制使用了MRC。这种技术中，不同天线元的信号根据它们SNR的比率进行结合。我们发现，不仅全部系统性能有提升，正如期望的，用于信道估计的符号可以使用更小的功率。

1.权重向量计算

式（7.4）中的权重向量w取决于使用的优化参数。对于波束成形减少MSE的权重向量公式如下:

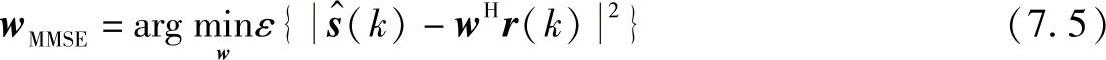
由此可以导出用于q的Wiener-Hopf权重向量

w_MMSE=R^-1p_q （7.6）

此处R=ε｛r（k）r^H（k）｝，用户q的传播矩阵是p_q（k）=ε｛r（k）s_q∗（k）ε｝。

在参考文献［NaCB03a］中分析了MMSE阵列处理器的SINR性能。如图7.1所示，对于高信噪比，干扰控制和阵列处理器作用很小，减少了干扰信号的组成。在低信噪比时，阵列处理器起控制作用，最大化来自目标用户的信号能量。在MMSE阵列处理器找到空值和波束方向的预期值时存在一个平坦变化的区域。

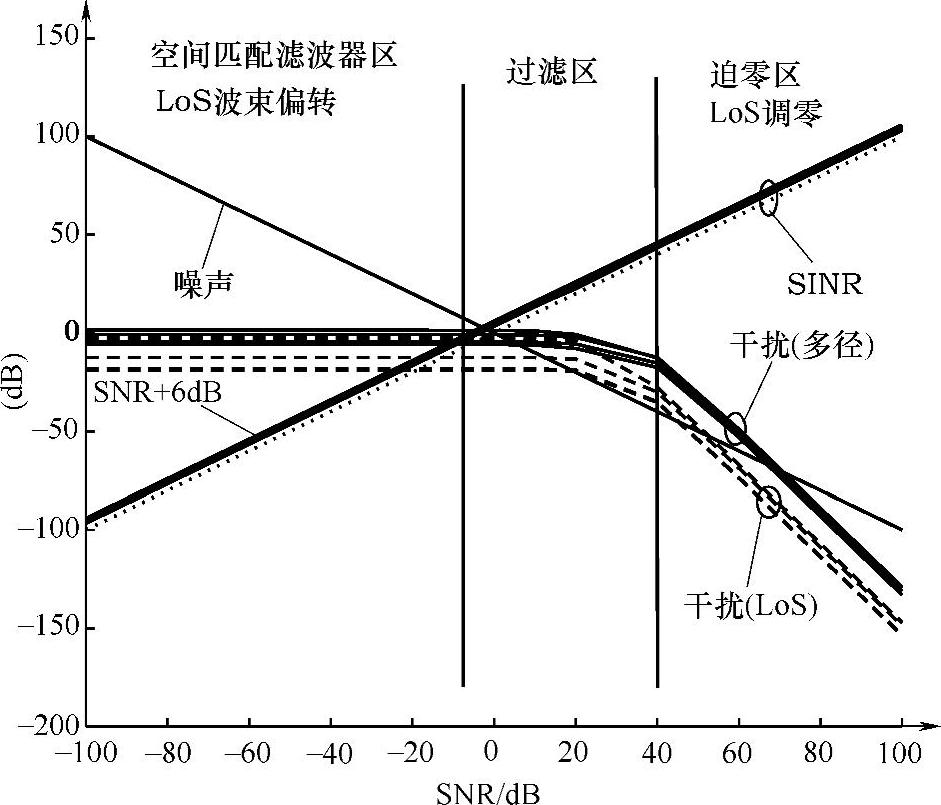
图7.1 噪声和干扰对比（SNR为MMSE矩阵权重，N_t=N_r=4）

当信道矩阵H是列稀疏时，例如，当矩阵轻负载（N_t＜N_r）时，信号成分r（k）的信号元的联合矩阵R_ss=Hε｛s（k）s^H（k）｝H^H，是不同的，噪声的影响可以通过使用基于子空间阵列处理器来减少（见参考文献［Will02］）。对于N_t≤N_r，HH^H至少有N_t个非零特征值，表示为λ_i，i=1，…，N_t。由于(www.daowen.com)

R=HH^Hσ²_s+σ²_nI （7.7）

可以写为

R=U_sΛ_sU_s^H+U_nΛ_nU_n^H （7.8）

此处Λ_s=diag（λ₁，…，λ_Nt）+σ²_nI，Λ_n=σ²_nI。U_s的列是Λ_s的特征值组成的特征向量，并且扩展了信号子空间。U_s⊥U_n的U_n的列扩展了噪声的子空间。由于需要的用户信号必须位于信号子空间中，MMSE的权重行列式为

w_ss=U_sΛ_s^-1U_s^Hp_q （7.9）

2.联合检测

对于JD，可以发现s＾（k）使用了ZF的权重矩阵，由信道矩阵的伪逆给出，例如参考文献［WeMe04］中

W_ZF=（HH^H）^-1H （7.10）

注意到这需要信道矩阵的参数，而不仅仅是式（7.6）和式（7.9）中接收信号的协方差矩阵。

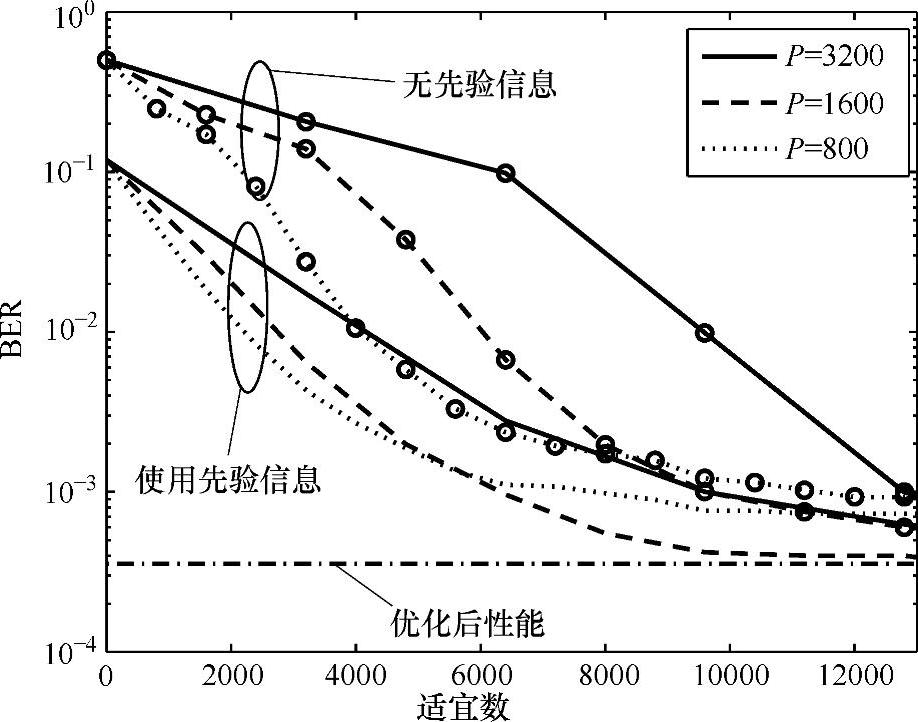
图7.2 BER与性能对比曲线（5天线，8用户，QPSK调制，SNR为17.8dB）

3.过载矩阵

当矩阵过载时，例如N_t＞N_r，ZF阵列处理器由于不能消除干扰，所以不能应用。这种情况下，ML-JD成为理想的接收机，但是对于m位/符号，复杂度为O（2^Ntm），复杂度则成为合理用户数目时的阻碍。参考文献［CoWi04b］中提出了对于复杂矩阵的联合检测的可选的方案，使用了ZF检测器提供的初始先验信息的遗传算法。在每一代，计算每个成员的适应度，下一代通过复制、变化、取优的过程产生。使用适应度的数目作为计算复杂度的标准，BER和复杂度的关系如图7.2所示，N_t为8个用户，N_r为5个元素的接收矩阵。使用先验信息的重要性在提高初始化性能和快速变换时。种群规模P，也会影响变化速度和逼近的性能。