在这一节当中，我们描述一般信道模型，该模型可用于产生双向脉冲响应（DoubleDirectional Impulse Response，DDIR），这是信道建模的最终目标。从这些双向脉冲响应中，仅仅需要明确天线配置以及链路两端天线单元的模式就可以得出任意的天线结构下的传输函数矩阵。参考文献［Moli04b］中讨论了如何获得传输函数矩阵;在参考文献［CCGH］中给出了一项标准天线结构的建议。

COST 273模型是在各种类型的环境下使用的一般信道模型。这是与COST 259模型很重要的一项区别。COST 259模型是在宏蜂窝、微蜂窝以及微微蜂窝中使用不同的通用模型。这是它与COST 273模型之间的一个很大的区别，可能不会产生最精确的模型结构，但它是一种对现实实现很好的简化。现实实现的许多方面都与COST 259模型中的宏蜂窝模型相似，如文献［StMo01］所描述，更详细的描述见文献［MAHS05a］和［AGMP05］。

该模型能够区分外部参数和随机参数，外部参数对于一次仿真运行是固定的，描述了仿真环境，也参与了随机脉冲响应的参数化，而随机参数是依据某个在不同环境中参数化了的概率密度函数选择出来的。

1.外部参数

如上所述，外部参数是在一次仿真运行中保持固定的参数。它们可能会根据仿真的系统以及地域（比如在北欧和日本，市中心的平均屋顶高度是不相同的）而改变。

（1）所有环境中的外部参数

以下参数在所有的环境中使用:

f_c（载波频率［Hz］）:对大多数蜂窝应用，载波频率在2GHz频带处，对于微微蜂窝和Ad hoc应用（无线局域网等），在5GHz频带处的载波频率更常见。

h_BS（基站高度［m］）:对于宏蜂窝和微蜂窝环境，高度指的是高于地面的高度。对于微微蜂窝，它表示从移动台所在地面往上的高度。负高度意味着基站处于比移动台更低的地面。

h_MT（移动台高度［m］）:在室外环境下，h_MT表示高于街面的高度，当移动台在街道标高处的时候，其典型值为1.5m。在室外到室内的应用中，h_MT会更大。对于微微蜂窝应用，h_MT表示从用户所在地面往上的高度，通常总是1.5m。对于Ad hoc应用，移动台的高度为0.8m（桌面高度）。

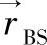（基站位置［m］）:指坐标系原点到基站的距离。正常情况下，基站是固定的，坐标为（0，0，h_BS）。但是，在Ad hoc和对等通信的情况下，基站的轨迹可以是规定好的。

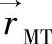（移动台位置［m］）:该参数描述了仿真运行过程中移动台在蜂窝内移动的轨迹。

天线场景情况（如4元素一维阵列）［天线的数目、天线间距、阵列形状］:系统的设计者对天线结构进行了描述，确认所使用的天线数目、天线间距、阵列形状以及天线单元的模式和极化方式。

天线方向［概率分布函数］:是在描述移动台运动的坐标系中天线方向的概率分布函数。

路径损耗模型［dB/m］:路径损耗是一个依赖移动台和基站距离的外部参数，即

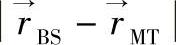。路径损耗通常由功率损耗（包括一个可能的断点）来描述。不同环境的精确表达公式在6.8.4节给出（直接或通过引用）。为了进一步的使用，我们同样将附加路径损耗定义为模型路径损耗和自由空间路径损耗的差值。

（2）宏蜂窝和微蜂窝的附加外部参数

对于宏蜂窝和微蜂窝，有几个参数描述建筑物的结构。当模型需要使用一些标准值时，可以对它们进行调整以适应具体的城市环境。

h_B（平均屋顶高度［m］）:典型市区环境下建议值为15m，闹区环境下建议值为30m，郊区环境下建议值为8m。

w_r（路宽［m］）:典型市区环境下建议值为15m，闹区环境下建议值为25m。

w_b（建筑物距离［m］）:典型市区环境下建议值为25m，闹区环境下建议值为100m。

Φ_R（相对于直射路径的道路方向［°］）:建议值为45°。

用这些参数来获得COST 259模型的最大兼容性。

（3）微微蜂窝和Ad hoc网络的附加外部参数

l_l，l_w（房间大小［m×m］）。住宅环境下建议为3m×5m;有独立办公室的办公环境下建议为2m×4m;有小隔间的办公室环境下建议为10m×10m;大厅环境下建议为50m×20m。

N_floor（移动台和基站之间楼层的数目［整数］）:标准情况下，该值为0，也就是移动台和基站处在同一楼层。

移动台和基站所在的建筑物对面是否有建筑物［是/否］:默认为是。

2.随机参数

随机参数描述移动台可能在的不同位置和无线环境。它们的参数化会受外到部参数的影响，如6.8.4节中的表格所反映。

依据参考文献［MAHS］中的概念，多径分量以簇的形式到达。总的双向脉冲响应可以写成簇的脉冲响应之和，用公式表示为（见参考文献［AGMP］）

P（τ，θ_BS，φ_BS，θ_MT，φ_MT）=P_τ（τ）P^B_θS（θ_BS）Pφ^BS（φ_BS）P^M_θT（θ_MT）Pφ^MT（φ_MT） （6.66）

注意此模型假设在一个簇内，在移动台和基站处的方位角扩展、仰角扩展和延时扩展是相互独立的。这不是普通的克罗内克模型，假设在移动台和基站处角度统计值相互独立，而在我们这里，独立性是对各个簇而言的。因此，在整体上DoA和DoD之间仍然能存在有效的耦合。

3.簇的生成——总论

COST 273信道模型的重要思想是通过几何方面的考虑对平均角度和簇时延进行建模。而簇内扩展和小规模衰落可以由几何方法或抽头延时线表示法表示。此原理也与COST 259模型相似。

关于这一点，区分电磁波经过单次干涉（文献中通常称其为单散射）从发射机传播到接收机的不同情境是很重要的（见参考文献［Corr01］）。单次干涉会在发射机和接收机处产生时延和角度之间的强相关性。对于宏蜂窝环境，单次干涉非常起作用，而在室内环境下时延和角度之间相关性则不存在。为了处理宽波段的情形，COS T273模型包括了3种簇:基站和/或移动台周围的局部簇，包含单次干涉的簇以及允许多输入多输出的双簇。在各种环境中不是所有种类的簇都是必需的。在宏蜂窝环境中，单次干涉簇是主要传播机制，而多次干涉过程在室内环境下占了所到达的大部分辐射能量。该模型最终指定一个“选择参数”K_sel，它给出了单次干涉与多次干涉附加簇之比。由于此时没有可供使用的度量，因此在宏蜂窝中令其为1，微蜂窝中为0.5，在微微蜂窝为0。局部簇仅仅体现出单次干涉行为。

4.簇的生成——局部簇

在移动台周围总是能出现一个簇，而在基站处的局部簇仅仅在某些环境中出现。这些簇分别在移动台或基站处引起较大的角度扩展。对于移动台和基站处局部簇，使用单纯的单散射方法。如下所述，局部簇的大小根据延时扩展和簇内的多径分量分布得到。

5.可见范围

在参考文献［MAHS05b］中解释了可见范围的概念。每个输入输出的簇与可见范围是相关的。如果移动台处在可见范围内，那么一个簇就是活跃的，且能够对脉冲响应起作用;如果移动台处在可见范围之外，那么簇便不会起作用。可见范围以下面的变量为特征:R_C为可见范围的大小［m］;L_C为传输范围的大小［m］。

非活跃簇到活跃簇的平滑转换由通过因子A²_m改变簇的路径增益实现。所使用的转换函数为（见参考文献［MAHS05b］）

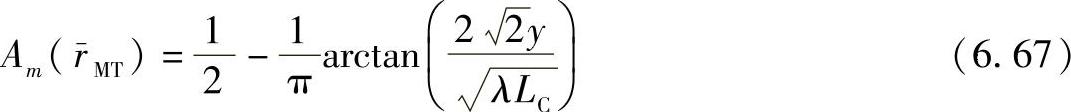
其中

式中，r_m是圆形可见区域的中心;λ是波长。

另外，可见范围还以其所在位置的概率密度函数为特征，该函数取决于可见范围到基站的距离。为了使簇数目的期望为常数N_C，可见区域的面密度应为（见参考文献［AGMP05］）

对位于一个可见区域内的簇的位置进行如下讨论。只要当移动台进入可见区域时，簇的位置就应该是固定的。产生的簇在空间中是固定的，并且它将在可见的条件下一直保持固定。

6.簇的生成——针对单次干涉簇的几何方法

对于单次干涉的情况，簇的位置用一种几何方法来确定。第一步，簇的可见区域分布在整个小区中。小区内可见区域的数目通常利用这样一种方式来选择，随机放置移动台来得到平均附加簇的数目N_C。每一个可见区域与一个特定的簇相关。注意，由于使用该方法，蜂窝中簇的总数目会变得非常大，但是在每一个时间点上只有一小部分簇可见（因此需要对其给予考虑以便于计算）。相对于基站位置的簇以及簇中心的位置通过下面的几何方法来确定:从基站到可见区域的中心画一条线，簇的位置将参考这条连接线来确定。到基站的径向距离依据指数分布函数确定:

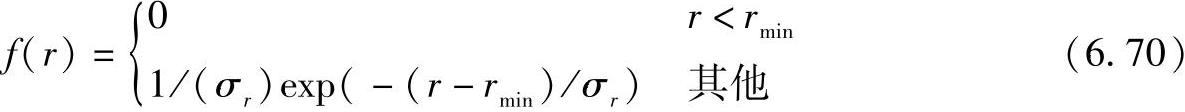
簇中心的角度依据服从标准差为σφ，C的高斯分布随机画出，这样就固定了簇的位置。时延（在这里假设为最小，虽然不精确）、从基站角度来看的方位角以及从移动台角度来看的方位角可以通过简单的几何关系计算出来。这些值将用于进一步的计算。

7.簇的生成——角度谱方法

对于多次干涉簇，平均DoA、DoD和最小时延以随机实现的方式根据其边缘分布计算出，较大的测量区域被取代。变量是从边缘分布中得到的，这说明延时和角度是相互独立的。但是，我们再一次强调，这样产生的模型并不是克罗内克模型，即角度时延功率谱是不可分离的。

现在考虑更为精确的公式。通过计算一个均匀随机分布数x，然后计算ϕ=cdf_D^-O1A（x）来指定簇的DoA，其中cdf_D^-O1A（x）是DoA的边缘累积分布函数，并且在较大的区域内对其进行平均（不要与小规模平均角度功率谱混淆）。对DoD和簇内时延τ_C重复以上步骤。下一步，为该簇指定时延扩展τ以及角度扩展φ_BS、φ_MT、θ_BS和θ_MT。所指定的时延扩展是移动台和基站距离的函数。DoA-DoA平面内簇的实现如图6.55所示。通过增加一个正交轴可以将其扩展至时延和/或高度域。

8.簇的生成——针对多次干涉簇的几何方法

在多次干涉的情况下，每一个簇被分解为一个与基站相对应的簇和另一个在移动台处的簇，如图6.56所示。由此而能够分别对基站和移动台处的角度色散独立建模。为了限制复杂度，相对应的一对簇就像“双胞胎”一样，具有相同的输入输出分布和长期的性能。另外，每一个基站簇的输入输出在移动台处都有相对应的一对输入输出。因此，多径分量的总数目就等于输入输出端的数目。一个簇内的输入输出端的分布将在6.8.3节中讨论。

图6.55 室内环境下拥有9个相同的簇的DoA-DoD谱

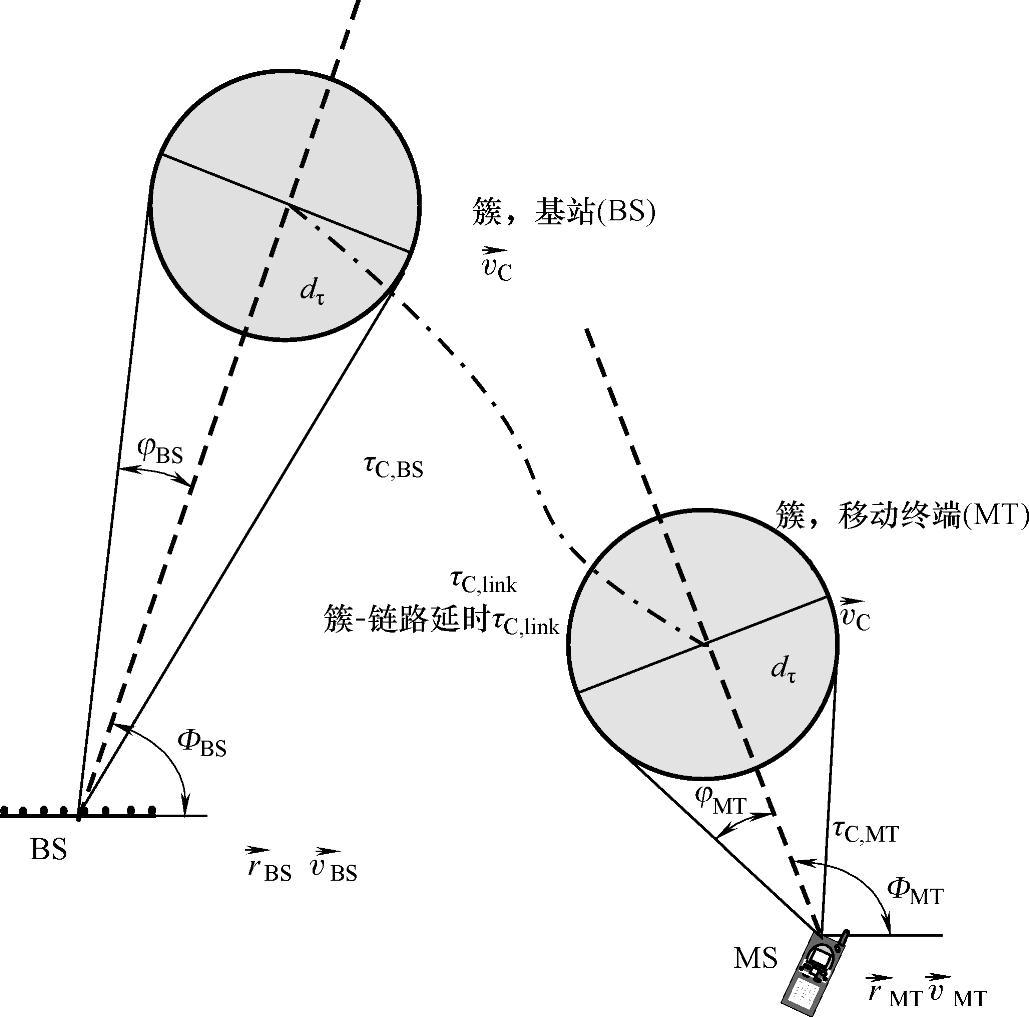
图6.56 二维平面下簇的分布

接下来的概念是关于如何根据以上假设对一个簇进行建模。大规模的研究是该模型的主要部分。因此该模型是基于空间中的示意图的。相比于时延-角度平面内的方法，这个模型是对移动台的运动和簇进行建模的。

第一步，指定基站和移动台的初始位置，如图6.56所示。与上面所述的角度扩展方法相同，簇的扩展和方向随机指配。簇到基站/移动台的距离作为随机参数d_C，BS/MT给出。如果该参数不可用，那么可以使用下面的几何方法。簇在空间中的位置用下面的方法计算:

其中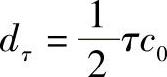。这就保证了在x、y方向的大小是相同的;但是应该注意参数化不是以物理参量为基础的。同样应该注意的是在讨论扩展和由此得出的簇的大小时，我们通常用σ-方均根扩展来表示。仿真时簇应该覆盖的面积约为3σ。图6.56展示了二维情况下簇的定义。簇的扩展可以在几何平面（如图中所示）或者时延-角度平面表示出来。从基站和从移动台处看到的簇的位置明显不同。又引入簇-链路延时τ_C，link，从而保证簇的总延时符合场景的定义:

τ_C=τ_C，BS+τ_C，link+τ_C，MT （6.72）

有可能簇的总延时出现负值（小于视距情况下的延时）。这种情况是人为造成的，应该通过对簇重新定位予以避免。这种情况主要是在起初簇距离移动台较远，但是后来移动台又靠近簇的时候发生。

簇数目N_C的分布函数通过均匀分布的N_C，min（对应于移动台附近的干涉产生的簇，可能还有基站附近的簇）加上服用参数为N_P的泊松分布的随机变量建立。

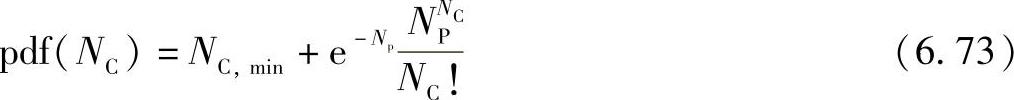
对于角度谱方法该分布函数用于获得簇的数目。对于几何方法，可以从移动台所处的可见区域的数目立即推断出簇的数目。选择可见区域的密度是为了得到每一种环境下簇的平均数目。(www.daowen.com)

9.簇的功率模型

每一个簇拥有的功率都是延时（相对于直射路径分量或者准直射路径分量来说）的函数。延时越大，它含有的功率就越小。但是对于簇的衰减是有限制的（如果衰减过大，簇对于脉冲响应没有影响，因此可以将其忽略）。第m个簇的功率为

P_m=P₀max｛exp［-kτ（τ_m-τ₀）］，exp［-kτ（τ_B-τ₀）］｝ （6.74）

式中，k_τ:衰减系数，单位为dB/μs;τ₀:直射路径分量的时延，单位为μs;τ_B:截止延时，单位为_μs。

10.视距情况

在一些环境中对视距情况是进行随机建模的。这种建模方法与簇的可见区域建模非常相似，因此不做详细描述。两者的主要区别在于视距发生的概率随着移动台到基站距离d_co的变化剧烈地减小，截止距离之后变为零。因此，用以下参数来描述该模型:

d_co［m］:视距条件下的截止距离。

R_L［m］:视距条件下可见范围的半径。

L_L［m］:对于视距可见范围的传输范围的大小。

视距功率因子（相比于其他所有分量的功率的第一分量的功率）根据视距连接存在与否来改变。不论在哪种情况下都将其建模为服从对数正态分布的随机变量，但是对是否有视距路径和准视距路径的情况，其平均值和方差是不同的。准视距情况描述了一种局部簇服从莱斯衰落的非视距情景，因而对弱视距分量进行建模。这些参数为:

μ_K:视距功率因子的均值

σ_K:视距功率因子的标准差

11.簇色散

双向延时功率谱（Double Directional Delay Power Spectra，DDDPS）（即双向脉冲响应模的二次方）以各个簇的在一些域中的色散为特征:时延、基站处的角度、基站处的高度。移动台处的角度以及移动台处的高度。

在时延域，使用一个以指数方式衰减的功率延时分布。指数分布以衰减常数στ为特点，该常数等于常见的方均根时延扩展:

时延扩展本身是一个服从均值为m_Sτ（ns）、标准差为S_Sτ（dB）的对数正态分布的随机变量。应该注意的是均值是随着基站与移动台距离的增加而变大（见参考文献［GEYC97］），这是由于:

在参考文献［Corr01］中，ε=0.5与一些环境的测量数据相符;而由于缺少任何其他（与之相矛盾）数据，所以对于所有环境都将其作为默认值。对于基站处的角度色散，使用拉普拉斯功率谱来表示:

其中，角度扩展σφ是一个服从均值为m_Sφ（°）、标准差为S_Sφ（dB）的对数正态分布的随机变量。相似地高度功率谱函数表示为

其中，仰角扩展σ_θ是一个服从均值为m_Sθ（°）、标准差为S_Sθ（dB）的对数正态分布的随机变量。

对于移动台，同样定义了角度参数。值得注意的是这些参数可能取决于簇延时。例如，对较早到达的分量（宏蜂窝中屋顶上方）和较晚到达的分量（沿着高楼间的街道）来说，其仰角扩展通常是不同的。同样，在某些环境中，对高度谱的拉普拉斯描述并不是最优的。

对模型的几何实现，在理论上将延时角度分布映射到输入输出分布上是可能的（见参考文献［MoLK98］）。在实际实现当中，没有必要求出精确的分布。参考文献［LaMB98］给出了单输入输出簇的大概的输入输出分布。对于双胞胎簇，输入输出使用截断高斯分布是可取的（在簇很小的时（θ_RMS＜14°）），该分布在角度域与冯·米塞斯分布相关（见参考文献［Fleu00］）。因此空间中的输入输出分布可依据下面的概率密度函数得出（这里是一维表达式）:

式中，x_T表示截断值。

选择x_T=3σ_x，从而确保几何整个高斯分布都在簇的范围内。由于定义簇在二维平面的大小为圆形、且在基站和移动台侧均相同，因此基站和移动台侧的簇可以使用同样的相对位置。为了修正独立的仰角扩展，通过除以基站侧的高度，将移动台处簇的输入输出高度修改为h_C，MT/h_C，BS。h_BS/MT表示簇的高度，用公式表示为

h_C，BS/MT=d_BS/MTtan（θ_BS/MT） （6.80）

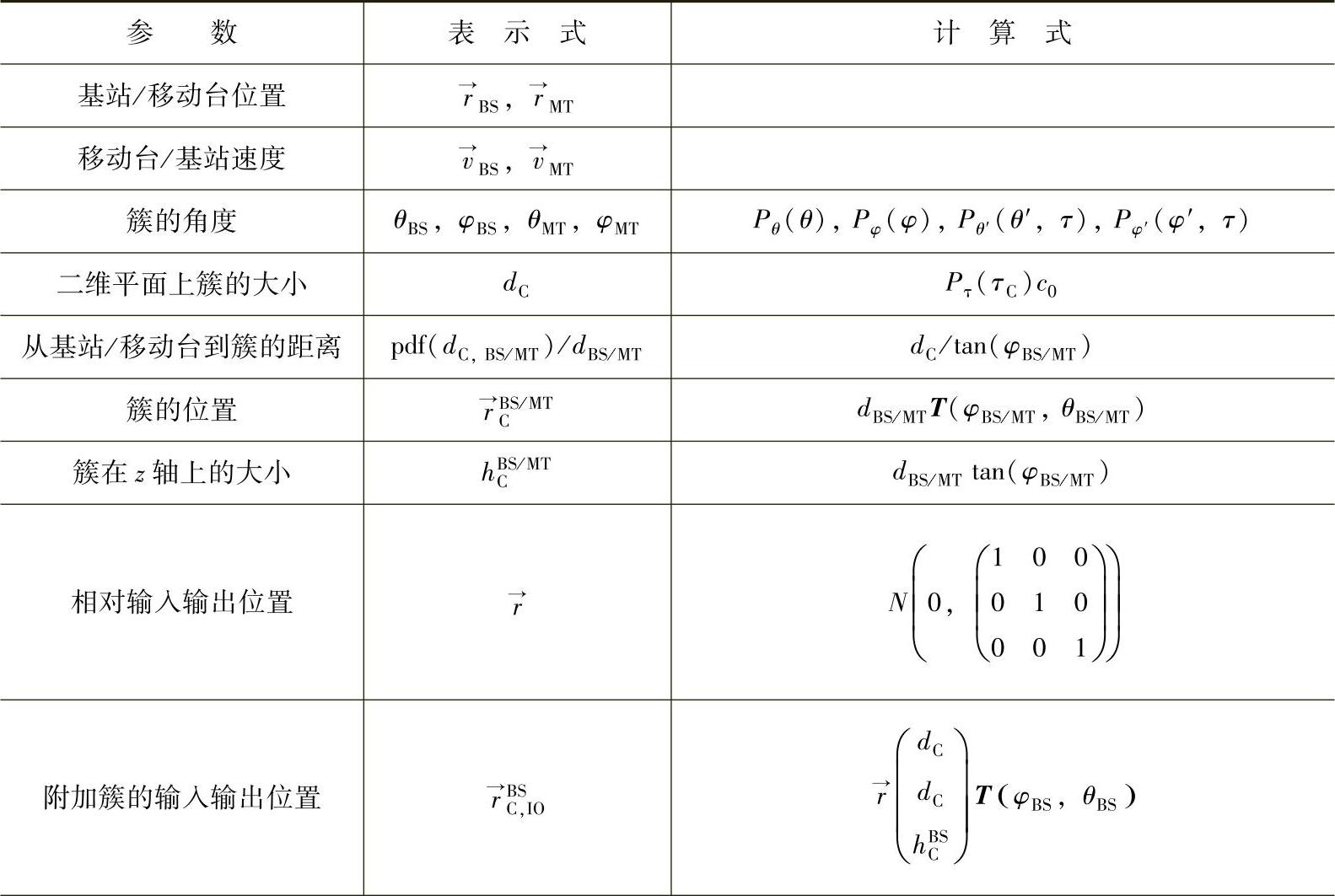
对于一个呈指数分布的功率时延谱，必须在基站和移动台处对簇进行旋转，使得它朝向基站，背对移动台，数学表达式见表6.6。多径分量的功率具有服从莱斯分布函数的特点:

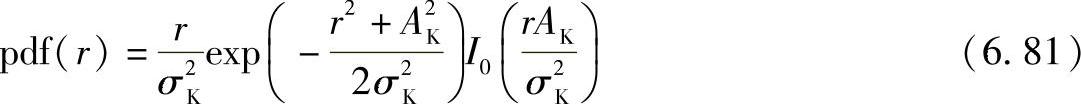
式中，I₀（x）表示零阶第一类修正贝塞尔函数;A_K是视距分量的幅度;σ_K是散射分量的方差。

莱斯因子为A²_K/2σ²_K，且与环境相关。

表6.6 多次干涉簇的实现

（续）

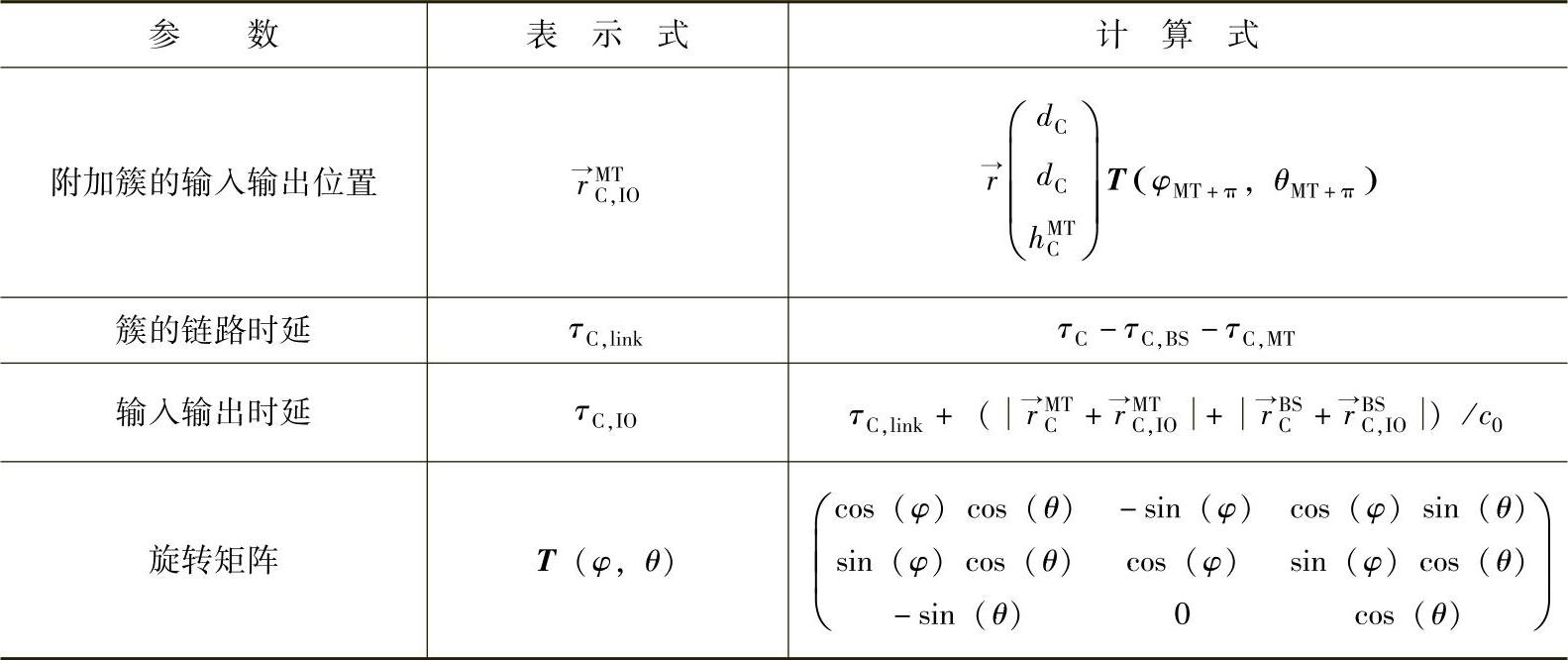
注:T表示空间中球旋转矩阵，P（n）为泊松过程。

12.阴影衰落

采用一种广泛使用的方法时，每一个簇都会经历阴影衰落，此衰落模型标准差为σ_S［dB］，服从对数正态分布。阴影变化的均值（见下面）与路径损耗相关。

13.自相关距离和互相关距离

阴影衰落、时延扩展和角度扩展都是相关的随机变量，表示为

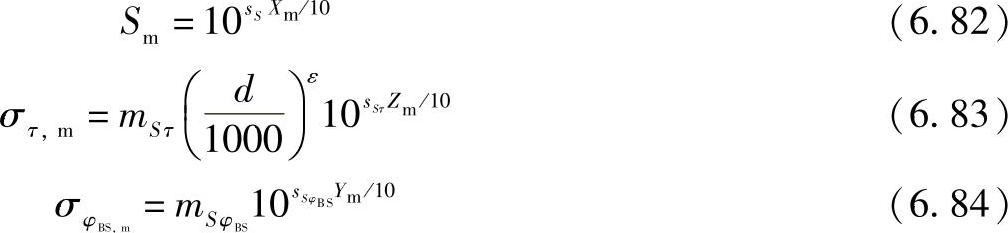
式中，S_m表示簇m的阴影衰落;στ，m表示时延扩展;σφBS，m表示基站侧的方位角度扩展。

X_m、Y_m和Z_m都是相关的均值为0、方差为1的正态随机变量。利用Cholesky分解（见参考文献［MoKl99］）对相关随机过程进行计算。可以将式（6.84）中的θ_BS、θ_MT分别代替φ_BS、φ_MT来计算移动台处的仰角扩展以及方位角扩展。我们最终能够得到6个对数正态随机分布变量，其自相关系数为ρ_ij，其中i=1…6，j=1…6。

另外，阴影衰落以及延时、角度扩展随着移动台移动很长距离而改变，因此用空间自相关函数来表征其特点，该函数是指数的:

ACF（x，x′）=exp（-x-x′/L_x） （6.85）

因此，不同的扩展值自相关距离L_x同样是重要的模型参数。

14.极化

由于极化的特点，正交极化会受到统计独立的小规模衰落，而所有其他的统计参数（如阴影、延时扩展等）则是相同的。因此，极化以极化矩阵为特征:

其中各个元素代表小规模衰落的平均功率，从此得到一个比值XPD:

是一个服从对数正态分布的随机变量，均值为m_XPD［dB］，标准差为S_XPD。与XPD的分布一样，所有其他的极化系数都建模为服从对数正态分布。XPD取决于收、发两端的距离以及多径分量的延时和角度。在一些选定的环境中，针对这些依赖性进行了测量（见参考文献［SZMS06］，［KLKK02］）。然而，这些结果不足以给出一个一般的参数化关系，因此不对它们做进一步的考虑。

15.固定无线系统的时变性以及移动应用

对于固定无线系统，我们需要定义时间因子K，它表示时不变多径分量的与时变多径分量的功率之比。首先，直射路径分量的因子K表示为

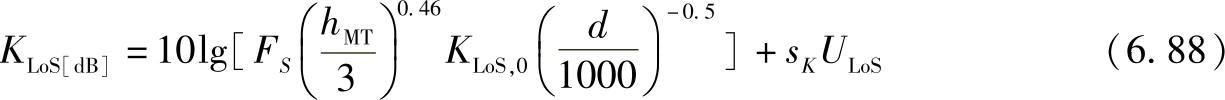
式中，F_S是周期因子，夏天（有树叶）时F_S=1，冬天（没有树叶）时F_S=1;K_LoS，0是待估计值（建议值为8～9）;s_K是标准差（6～8dB）;U_LoS是正态变量。

注意我们指定用户终端的高度为h_MT，尽管它很明显是一个定值。

第m个簇的K因子K_m表示为

K_m［dB］=10lg（m_K）+s_KU_m （6.89）

式中，m_K是簇的平均K因子;s_K是标准差（6～8dB）;U_m是一个高斯变量，与X_m、Y_m和Z_m相关。

簇的平均K因子表示为

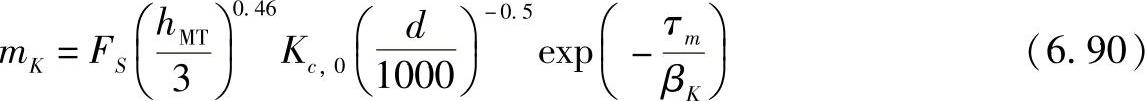
式中，K_c，0是待估计量（建议值为0.5）;β_K的估计值为1.5dB/100ns（对于最高频率为10MHz的带宽来说）。

16.漫散射

漫散射为测量信号的一部分，它是一个并不能在角度域得到解决的问题。最初的结果在参考文献［ThRi05］中可见。漫射分量可以用离散分量的功率与均值为_μdiff、标准差为σ_diff的漫射功率之比来描述。对漫射分量的功率延时分布进行建模，其角度呈均匀分布、延时呈指数分布。