MIMO建模中，空间相关性是波形传播的输出参数，同时也是容量计算的输入参数。空间相关性很早是用来减少MIMO系统的容量增益的，因此相关性在模型验证中应该作为重要的量。

1.几个相关系数

首先，能够清楚地区分几种相关性度量是十分重要的，即复相关性、包络相关性以及功率相关性，因为现在的一些文献在描述MIMO信道特性时，关于到底使用哪一个相关系数常常出现混淆。第二，相关性的种类有待澄清。在接收端、发送端或者链路中，天线单元处的信号之间会具有相关性。应该特别关注一种特殊的横穿链路的相关性，称作“对角”相关性，因为它可能提供比独立同分布信道情况下更高的信道容量，如下所述。参考文献［KCVW03］对相关性系数做了澄清。令u、v为两个复变量，比如复基带下的天线信号。复相关系统定义为

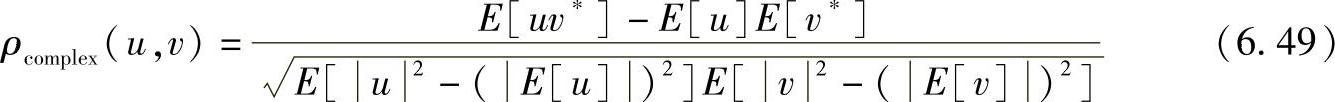
包络相关系数定义为

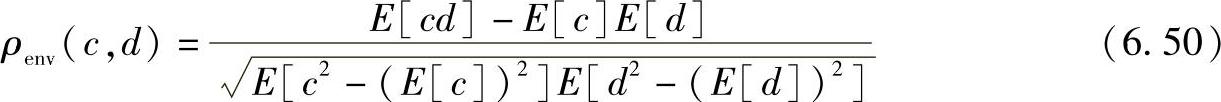
其中c=u，d=v。功率相关系数定义:

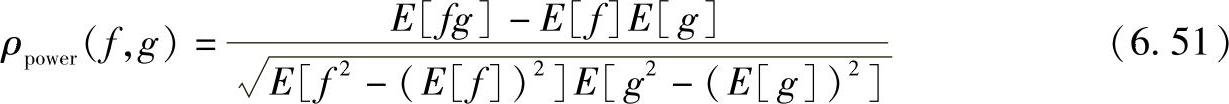
其中f=u²，g=v²。

复相关系数是复数，而包络相关系数和功率相关系数是实数。但是，它们的绝对值均小于1。对于高斯随机变量来说（见参考文献［LaZo96］），可以进行如下的近似:

ρ_env≈ρ_power （6.52）

ρ_power≈ρ_complex （6.53）

在MIMO系统中，受关注的量是信道容量和影响最终结果的变量相位，其中复相关系数是最受关注的（MIMO系统中，转移矩阵H的元素h_ij是复随机变量）。

2.对各相关矩阵进行比较

空间相关性是由传播环境和阵列结构通过到达阵列的多径信号功率角分布、单元类型以及间距共同决定的。虽然阵列结构可控，天线阵列单元的空间相关性是关于阵列所处的特殊环境的函数并且已经成为众多在单阵列系统中的研究的主题。

各种度量可用于通过模型和测量得到的相关性数据的比较当中。使用参考文献［YBOM01］中所述的方法，定义估计相关矩阵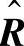和信道相关矩阵R_H之间的差值或者误差为

(www.daowen.com)

可以将ψ（X，Y）看作通过使用简化模型比如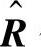做出的初始假设的有效性指示。

Herdin（见参考文献［HCÖB05］）最近提出另外一种相关矩阵的距离度量方法。为了获得在两个相关矩阵是完全相同的（标量因子除外）情况下值为0，在两者差异最大的情况下值为1的度量，定义相关矩阵R和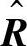的距离为

在这里，tr｛｝表示矩阵的迹，而·_F表示矩阵的Frobenius范数。可以很容易地通过另外一种形式理解该度量的含义:

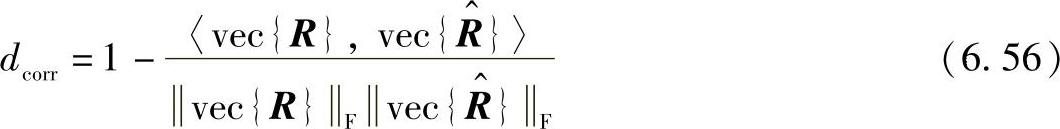
分别对通过测量和模型得到的相关矩阵进行vec运算，计算两个向量的内积，则约束最小化设计（Constrained Minimisation Design，CMD）与该内积直接相关。如果相关矩阵相同，CMD为0，相关矩阵之间差异越大，CMD值也越大。最终当差异达到最大时，CMD值变为1。如图6.53所示在拥有两种不同传播方向、综合的时变传播环境下的CMD值，计算在每一时刻各自的相关矩阵并且将其分别与第一时刻的矩阵进行比较。仅当一半环境改变时，CMD值精确反映了开始和结束时刻的相关性差异（CMD=0.5）。

CMD的优点在于它能够度量矩阵构造上的差异，以及改变像所使用的特征模的数目之类的功率或者系统参数值之间独立性。使用了后者的度量将在6.7.7节中讨论。

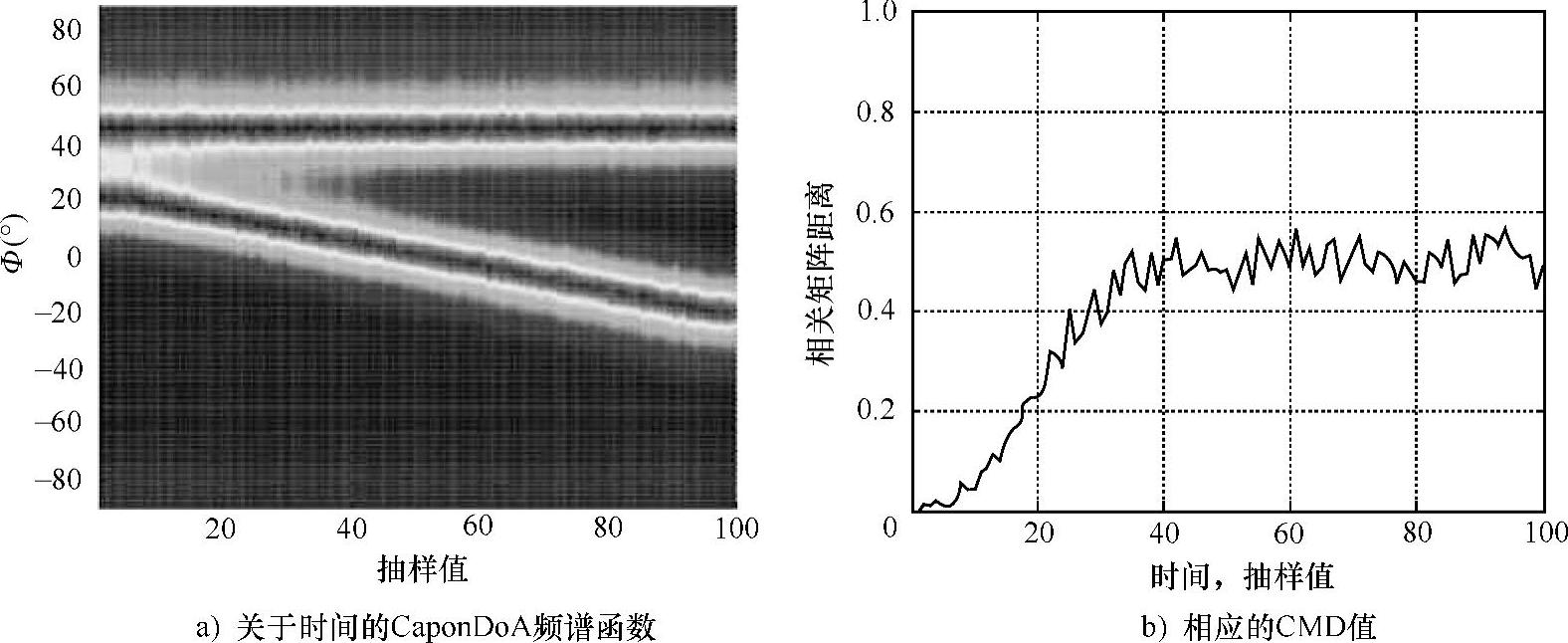
图6.53 综合的时变传播环境下的相关矩阵距离d_corr（见参考文献［Herd04］）

3.具有交叉链路相关性信道的容量度量

一个新的对交叉链路相关性的度量由对相关信道的各态历经容量的近似演化而来（见参考文献［OePa04］，该度量归类在上面的模型目录（iii）之下。在这里对模型验证使用相反的方法:用简单几何分布模型来验证新度量的有效性。依据式（6.35），度量表示为: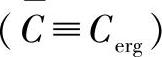

其中下标w表示不相关的情况，行列式—k定义为

由log₂是单调函数可知，在该度量中C—和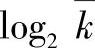的作用是相似的。C_w和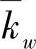用来消除由于对行列式求期望以及log₂操作引入的固定偏差。容量C—_w的解析表达式在很多文献中常常可见，并且通过一次蒙特卡罗仿真即可得到。另外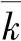，与完全相关矩阵R_full唯一相关［如式（6.34）所示］。

对所谓的对角相关的2×2MIMO信道矩阵求行列式，根据结果可以得出这样惊人的结论:独立衰落并不能使各态历经容量最大化（见参考文献［OePa04］）。因此空间相关性是一个令人迷惑的量，而且它确实能够提供一些非常有趣的度量。