尽管很早就认为信道的多径丰富度对于MIMO来说是很重要的，但是能够被广泛接受的对信道这一属性的度量是很少的。COST 273中出现了一些新的概念，其中的一些应用到了窄带模型当中，另外一些同样应用到了宽带模型中。

检验MIMO窄带模型的一个最简单的方法是通过DoD-DoA联合角度功率谱（Angu-lar Power Spectra，APS）研究一个MIMO信道的双向多径构造（见参考文献［Özce04］），它可以利用Capon波束成形方法计算，该方法又称为最小方差方法（Mini-mum Variance Method，MVM）（见参考文献［CaGK67］、［Capo69］）。

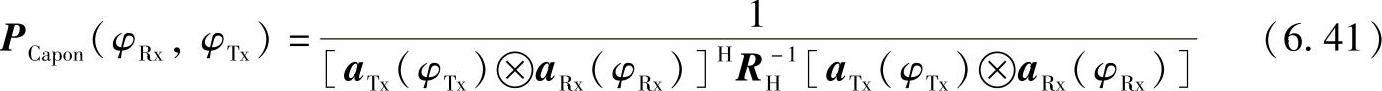
将导向向量a_Tx（φ_Tx）向着φ_Tx方向、a_Rx（φ_Rx）自φ_Rx方向进行归一化。由一维Capon波束成形法计算出单边边际谱（DoD、DoA）:

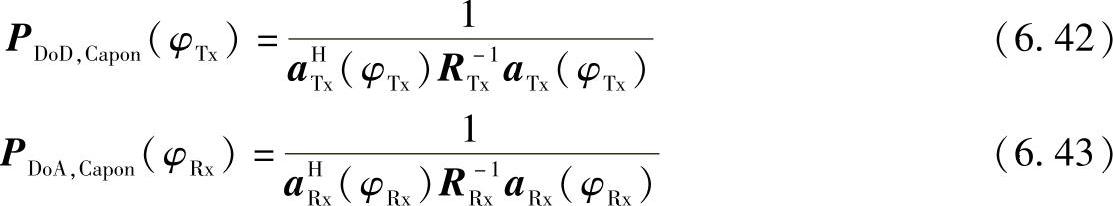
6.5节有对8×8MIMO模型进行验证和分析的一个举例应用。

为了找到包含单数容量附加信息的MIMO信道多径丰富度度量，Andersen（见参考文献［Ande04］）在大信噪比或者大特征值的限制条件下建立了容量等式［见式（6.35）］（消去了“1”对于I的影响）。得到的丰富度曲线（向量）定义为特征值的对数和:

去掉根据信噪比可以很容易计算出的常数项，容量便等于丰富度了。无论发射机处在哪一端，丰富度都是相同的。对特征值进行降序排列。图6.51为在奥尔堡大学不同的室内环境中使用16×32阵列的测量举例应用。因此可见丰富度定义似乎是不同环境和MIMO阵列对照比较的一个有用工具。图中画出了仅在整数特征值处定义的丰富度的曲线。

由于矩阵可以表示为延时的函数，因此将此定义扩展至宽带情况下，并且在固定位置处估计出作为延时函数的丰富度。在图6.52表示的测量例子中，在延时较大情况下，丰富度会增加。

参考文献［GiCo04］中详细叙述了一种完全不同的多径丰富度度量。它是基于到达信号的角度ρφ和时间密度ρτ，且这两个量在宏蜂窝和微蜂窝环境中差别非常大。一定要注意ρφ和ρτ相反地反映出丰富度的情况。用下式进行定量的丰富度测量:

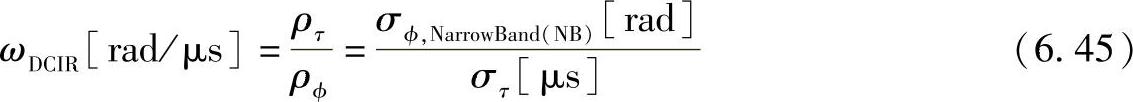
单位为rad/μs（考虑到它的维数，将ω_DCIR也叫做多径频率）。σ_ϕ，NB为接收端处的窄带均方根角度扩展。定义式（6.45）似乎矛盾地说明了时延扩展越小，多径丰富度就会越大。而我们期待出现相反的情况。但是ω_DCIR是单位时间内的平均量，并且时延扩展越大，暗示了更多时间单元内的相对角分量，同时反映出了较高的多径丰富度。如果在较小的时间段内、时延扩展较小的情况下到达相同的重要角分量，那么同时在角度和时间域中，ω_DCIR增加则反映出了高的多径丰富度。由式（6.45）得出的信道多径丰富度会对波束成形和干扰抑制都产生影响。(www.daowen.com)

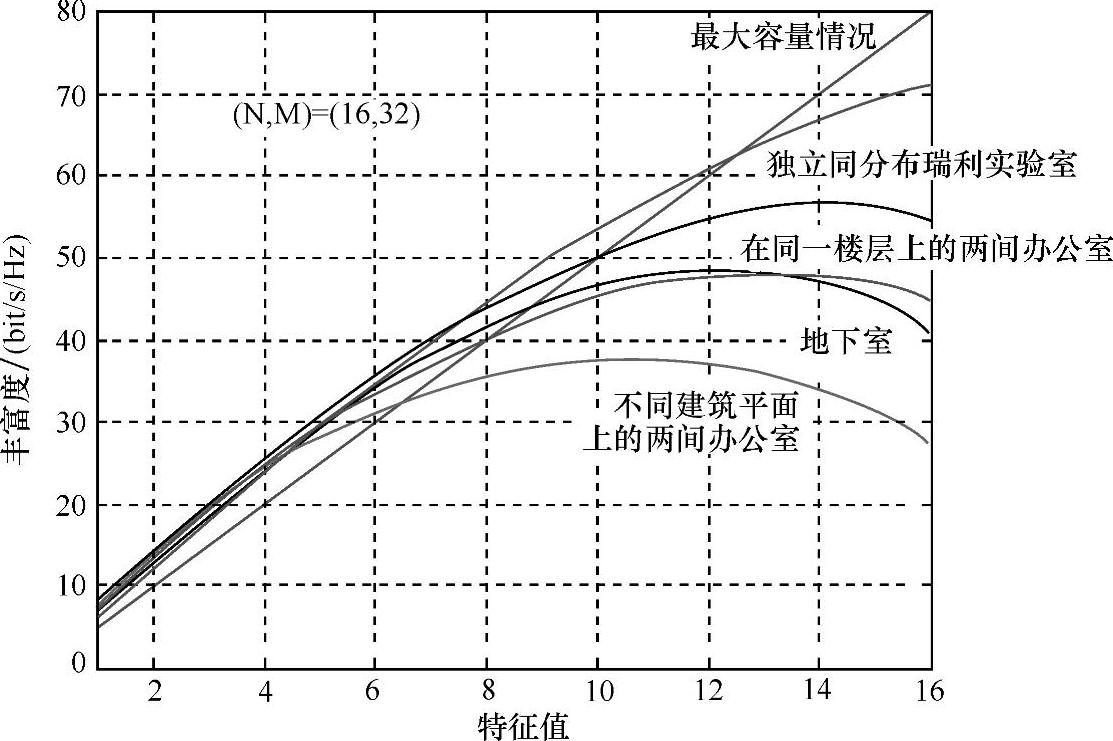
图6.51 16×32MIMO信道在不同环境下的丰富度，包括独立同分布瑞利和相同特征值时的最大容量情况，实验环境为:实验室（拥有全部的实验设备）、一个很空的地下室房间、在不同建筑平面上的两间办公室之间组成的链路、在同一楼层上的两间办公室之间组成的链路（从信号峰值处-30dB之下的信号都忽略不计）（见参考文献［Ande04］）

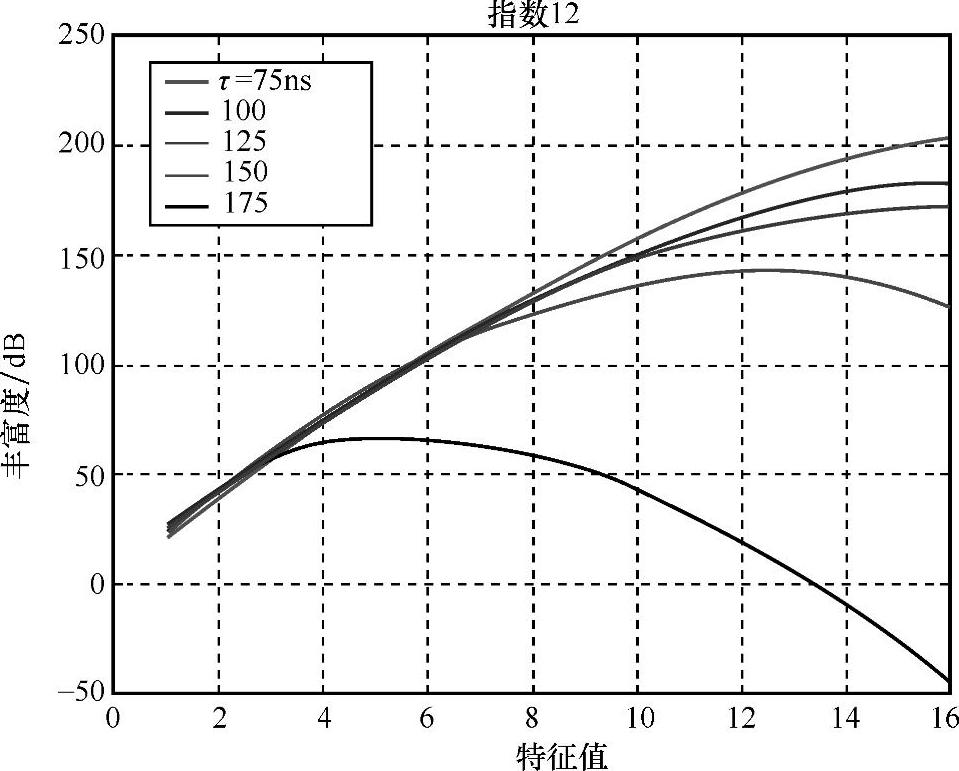
图6.52 在不同建筑平面上的两间办公室之间组成的链路丰富度，它是关于延时的函数（见参考文献［Ande04］）

参考文献［Egge03］试图将角度色散和时间色散与单个度量联系起来。结果是具有探索性的:

为了表示并行信道的随机性或者双重散射丰富度支持，它给出了最简洁的环境描述。Λτ是关于归一化的平均时延τ_norm的量:

其中，τ_inv可表示为

通过这样的方式构造时延扩展似乎很奇怪。这并没能暗示时间色散程度，即在与频率选择性衰落相关的一般情况下，仅仅说明了相对直射路径（LoS）的散射簇偏移，由此而暗示了平均路径偏移以及发射端和接收端之间散射区域的中心存在的可能性。该度量的角度量Λ_joint是基于双向环境函数的并且与从收、发两端来看散射体联合分布的中心偏离度的探索性描述相关。收、发两端中，当Λ_joint=1时，两端信号全分散，当Λ_joint=0时，在一端信号全分散，另外一端信号定向，当Λ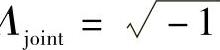时，两端信号都定向。其中后一种情况是在信道为非平行的情况，也就是钥匙孔信道实现。因此，虚数值暗示了信道的平行性较差和分集增益较低，0值说明了仍然可以获得分集增益，1值说明能够获得的分集增益是最多的。6.7.6节对于分集做出了详细说明。