容量已经广泛作为MIMO信道空间复用潜能的一种度量。假设所有天线发射功率相同,则依据测量结果可估计出各态遍历容量:
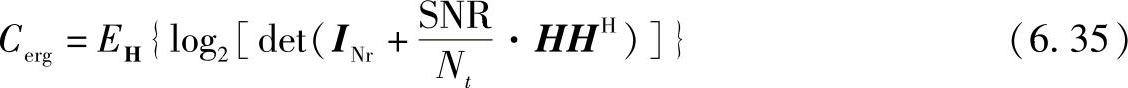
其中HHH是测量实例,或者对HHH进行实例化得到的瞬时容量值分布,或者对以上容量公式的近似处理得到的容量值。或者使用另外两种方法,避免使用容量,用统计特征值来代替。
实际当中要对所有新建立的模型,关于它们是否能够正确预测各态历经容量(互信息)进行验证。例如,图6.46a展现了通过测量和“克罗内克”模型预测得到的信道容量之间极高的一致性。但是,不能把通过模型综合处理与测量得到的容量值之间的高一致性当成一种模型有效性的一般证明。考虑另外的情形,图6.46b中展现了很大的偏差:模型的容量远低于测量容量(见参考文献[ÖHHB03])。
对传播激发模型的适用性进行研究以预测固定无线链路上的不同MIMO信道响应对范围的依赖性,除了其他度量,参考文献[OeEP04]使用中值容量作为一种度量(见6.7.8节)。中值容量可以从容量分布中得到(如方法(ii))。
除了使用预测得到的容量外,还可以根据特征值分布使用多种方法对模型进行验证。我们都知道,MIMO系统容量是由HHH的特征值决定的,由于HHH与HHH具有相同的非零特征值集合,所以两者是等效的(见参考文献[Burr04b])。可能用到方法(iv)中HHH实例或者方法(v)中的平均自相关矩阵的特征值分布。
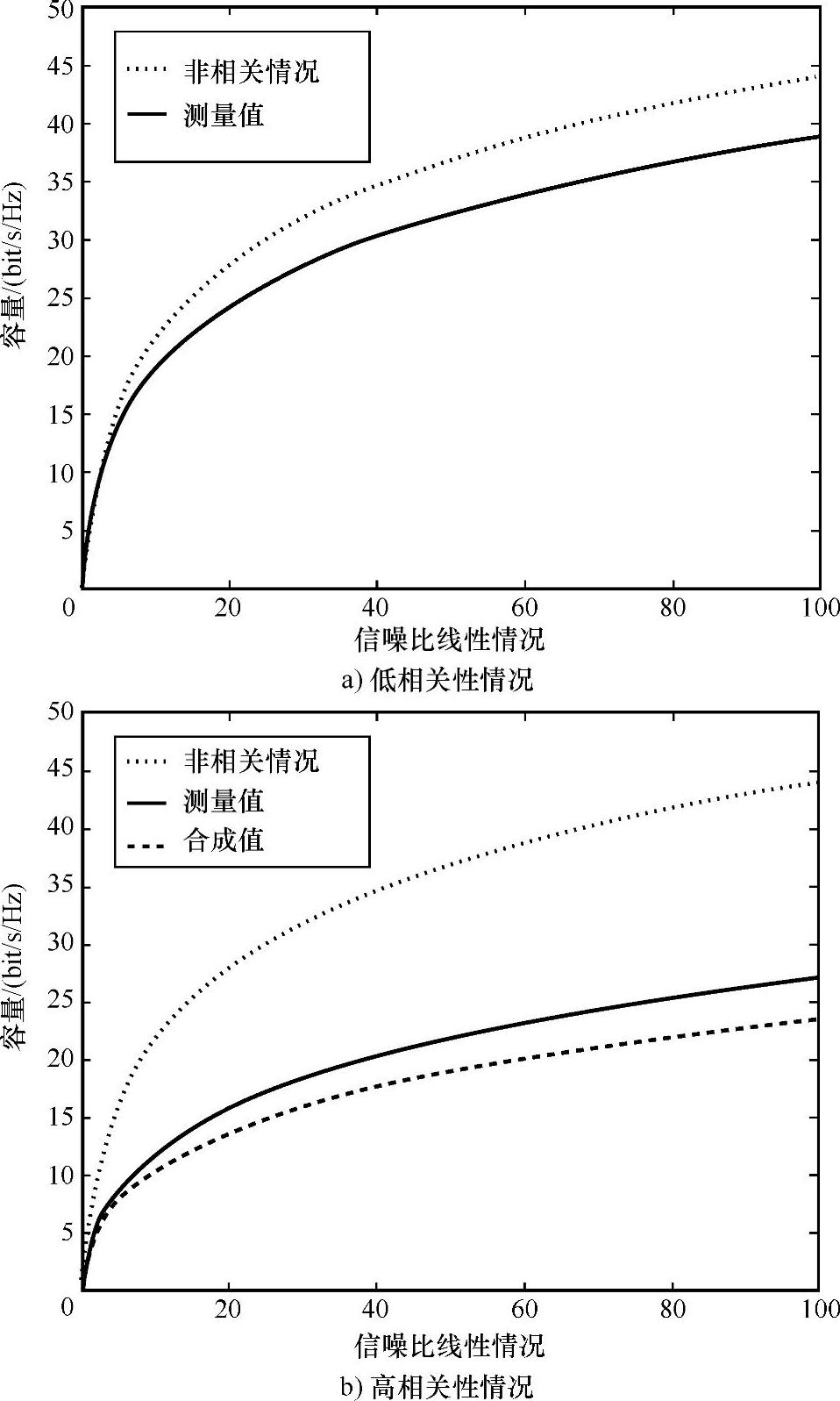
图6.46 信噪比-平均MIMO信道容量(通过测量与克罗内克模型预测得到的值)关系曲线(见参考文献[ÖHHB03])
若矩阵HHH的元素是随机的,常常将这种形式的矩阵叫做Wishart矩阵。根据该Wishart矩阵计算得到的容量累积分布函数或者互补累积分布函数,可以作为给一个利用方法(ii)验证模型的例子。图6.47表示在具有平坦的频率响应、相关瑞利衰落信道下,多天线系统容量的近似解析表达式是如何通过蒙特卡罗仿真得到验证的。
Eggers(见参考文献[Egge03])对关于容量及其度量的理论,即假设调制星座和适应能力具有无限灵活性,从而实现潜在的巨大信道容量(而这在实际当中是不可能发生的),进行了批判。这些度量同样地取决于参考信噪比,即这些都是绝对度量,则区分复用潜在增益和纯粹的链路增益就变得十分困难。相反,他提出两种相关的度量。首先,用归一化累积特征信道增益表示的并行性定义为归一化并行信道增益(Normali-sed Parallel Channel Gain,NPCGq),给定的中断级为q,
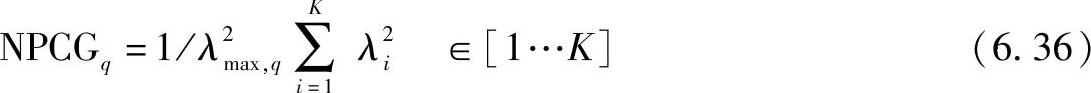
式中,K为空间正交子信道的数目,K=min(Nt,Nr)。它能够反映出环境(包括天线阵列的结构)的多路复用潜能。但是,由于线性额定功率总和的影响,相比于信道容量NPCG对特征功率差异不敏感。一种可选择的基于容量的度量,通过没有反馈端的MIMO系统容量相对实现,表示为特征值之和:

在高信噪比或者特征值的条件下,上式可以近似地展开为
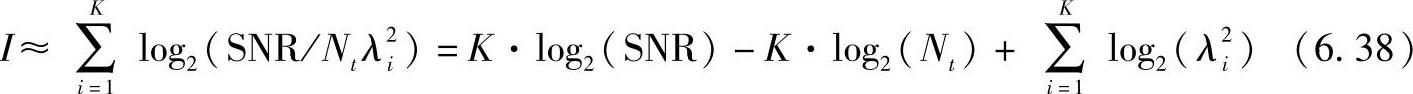
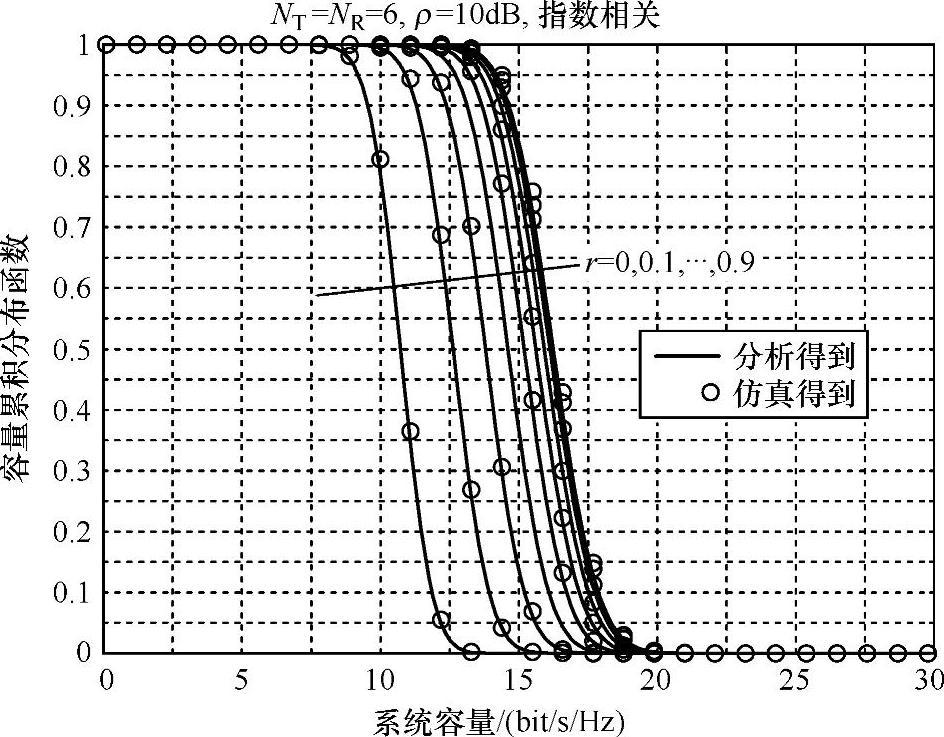
图6.47 实现关于MIMO系统容量的累积分布函数,[其中NT=6,NR=6,每根接收天线的信噪比ρ=10dB,对于指数相关性,r取从0~0.9,分别对获取分析和仿真得到数据的比较(见参考文献[ChWZ03])](https://www.daowen.com)
为了使用统一标准对不同阵列星座进行比较,对第一、二项进行降阶以实现归一化并行信道容量(Normalised Parallel Channel Capacity,NPCC)。较低的特征值(<1)可能会导致产生较大的负对数从而舍去该度量。由于加了数值“1”,所以所有的特征功率值是有偏的。NPCC近似表示为
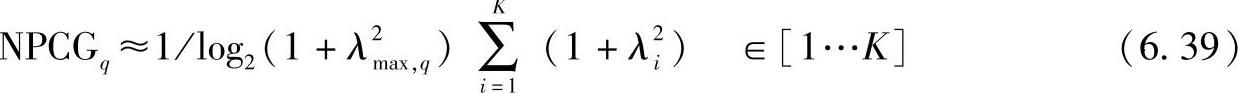
在使用自适应受限或者固定调制解调器情况下,NPCG和NPCC比纯粹容量都能够更好地体现出MIMO的潜能。
利用特征值统计信息[方法(iv)]进行一次验证(见参考文献[LiDe04a]),进而很好地区分基于分布的度量和单数度量。对分布情况进行比较是一个棘手的问题。在考虑分布的情况下,图6.48对经过测量与克罗内克模型综合处理得到的特征值进行比较,并且揭示出确定度量值高度是否一致的难度。为了量化一致性,必须借助于单个数目。通过下式,在特征为1、2、3、4时,计算出百分偏差分别为8%、7%、6%和10%。

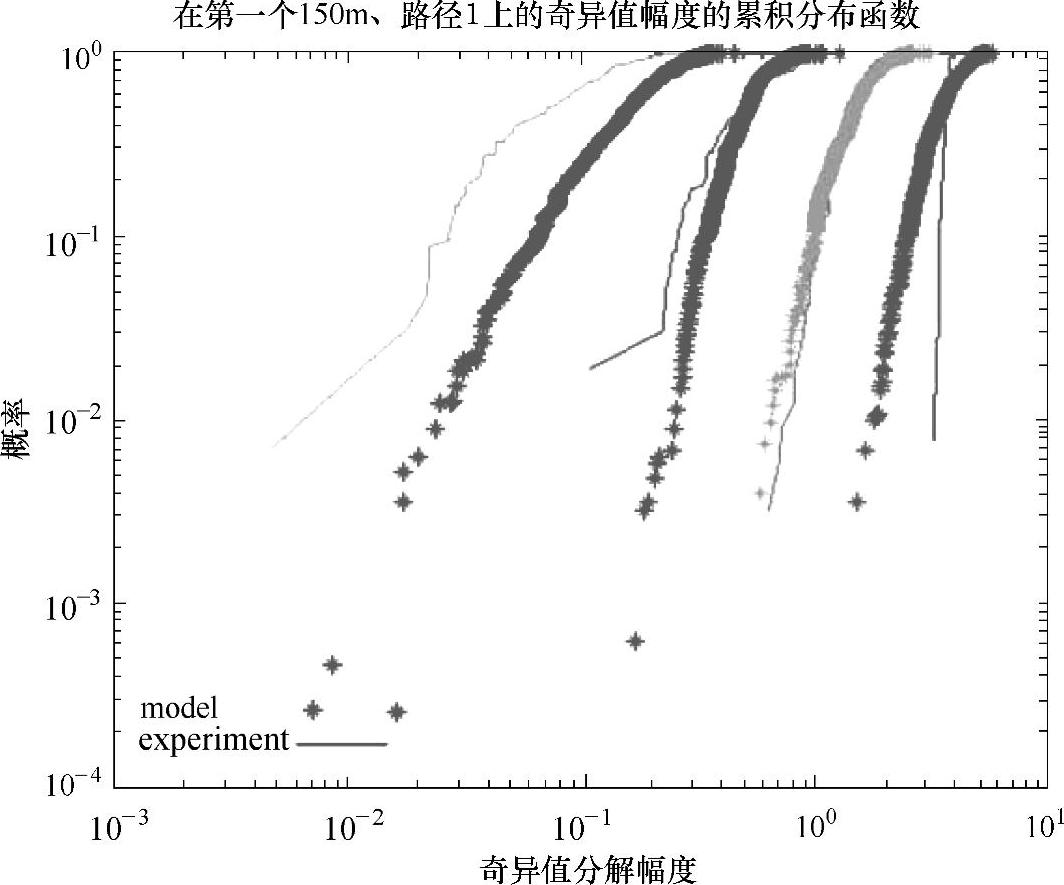
图6.48 在4×4MIMO系统中对经过测量与克罗内克模型综合处理得到的特征值进行比较(见参考文献[LiDe04b])
各态历经容量与中断容量
将各态历经容量与中断容量区分开来是很重要的。容量分布的方差值[方法(ii)]体现了容量互补误差函数的图的陡峭性。在宽带MIMO信道模型(见参考文献[McBF02b])的验证中重点突出了这个区别。图6.49针对不同的带宽1.25MHz、5MHz和20MHz,概括了8×8MIMO系统容量的测量和仿真的结果。注意这几点,首先,清晰的归一化和绝对容量的区别在于,对信道相应归一化能够在空间和频率域上去除平均路径损耗。(由于平均路径损耗对于MIMO性能有很大的影响,因此归一化并不总是适用的(见参考文献[MBFK00])。这说明了在恒定信噪比下使用归一化信道容量作为度量估计不同带宽信道性能的时候能够产生误导性结果)。其次,与仿真信道形成鲜明对比的是,不同带宽的归一化信道图形曲线变化是非常小的。随着带宽的增加,曲线的改变几乎不可见,仅仅在弯曲处有微小的改变。对于数目较少的天线单元,带宽的改变会对归一化信道容量影响较大。当信道带宽增加时,附加频率分集方法会对采用空间分集的系统带来更多的益处。采用独立同分布瑞利衰落模型会引起测量和仿真信道之间大的差异(多个延时之间的信道系数是不相关的)。在天线单元之间引入空间相关性一定会使信道模型接近于测量得到的信道,但是在宽带信道中,对于不同的延时抽头,其空间相关性也会不同。图6.50画出了前6个延时抽头的相关系数。每个图中8×8个方块值代表hij和其他元素的互相关性。
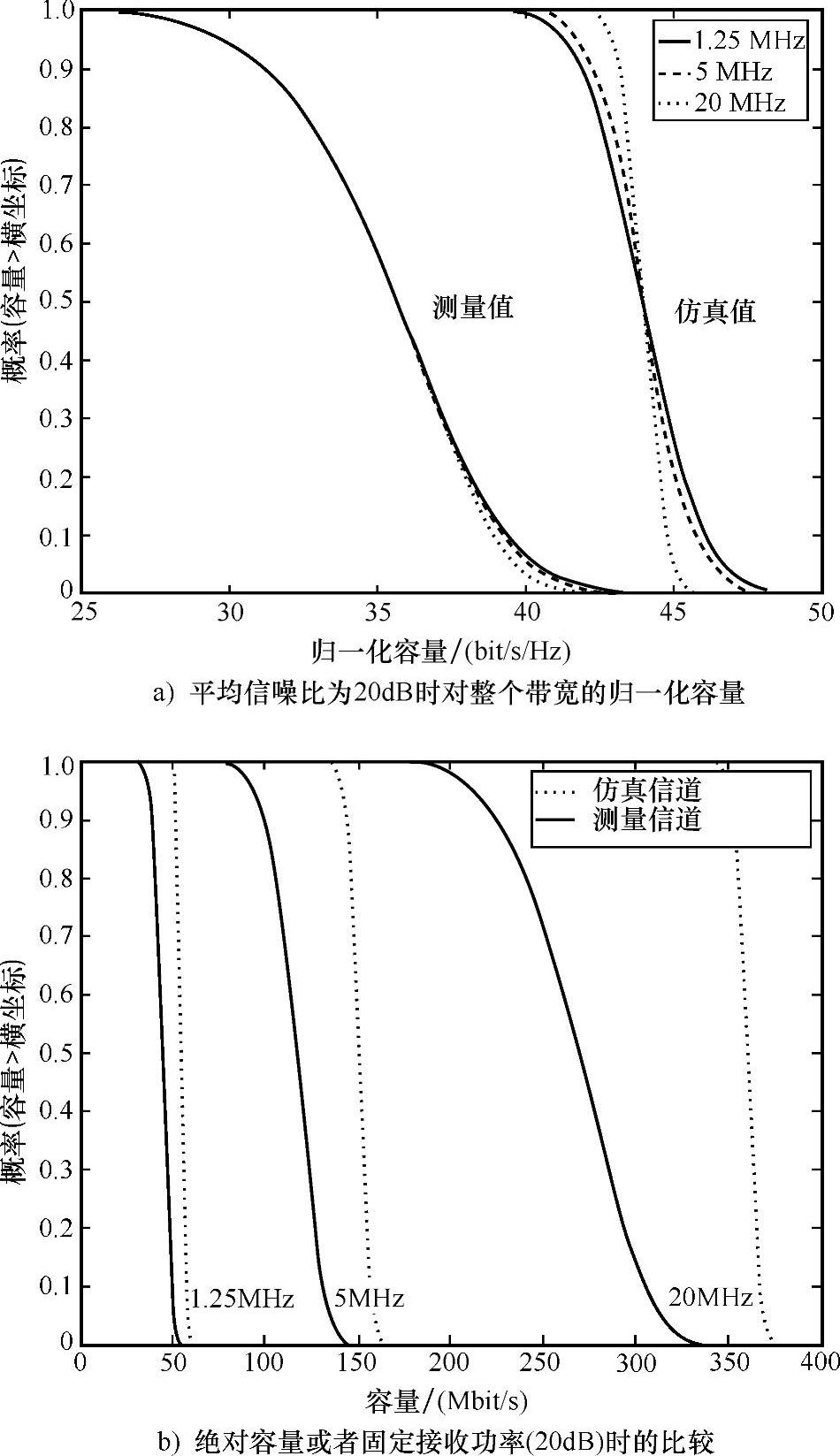
图6.49 不同带宽1.25MHz、5MHz、20MHz下8×8测量和仿真得到的MIMO信道容量互补累积分布函数比较(见参考文献[McBF02b])
通过模型和测量分别得到的容量曲线在弯曲度上有区别是一种常见、有趣的现象,从它可以看出这样的问题:在模型验证中,应该对各态历经容量还是中断容量进行匹配?
在式(6.35)的近似表达式中,可推导出一些更多的度量,其中的两个度量将分别在6.7.4节和6.7.5节中讨论。

图6.50 8×8MIMO信道矩阵H各个元素之间的互相关系数
a)~f)为冲激响应前6个抽头的系数矩阵)(见参考文献[McBF02b])
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








