1.有限散射模型

有限散射（见参考文献［StMB01］、［Burr03］）模型的基本假设，是发射机和接收机是通过由于离散散射器导致的有限数量路径n_S进行耦合的，因此信道矩阵可以写成

式中，☉表示Schur-Hadamard乘法;矩阵A_TX（n_T×n_S）和A_RX（n_R×n_S）表示矩阵，其列向量是和每个散射对应的导向向量;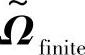是一个（n_S×n_S）的耦合矩阵，其元素是独立的复路径增益。

注意，除了标量的缩放，导向向量在任意给定的固定场景下是确定的。他们通过无线电波的DoD/DoA、几何数组以及元素模式来完全确定。但是，DoD/DoA以及路径的数目在确定的场景下是可以任意选择的。还必须指出，这个模型在路径增益上是线性的，但是在DoD和DoA上不是。这个模型和单散射的假设是兼容的，而在那种情况下，A_TX和A_RX可以重新排列从而使得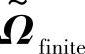是对角矩阵。考虑式（6.26）应用到多散射情况，存在两种定义。该方法的原始版本是通过在耦合矩阵的行/列各自的多项来处理多散射。COST 273（见参考文献［Burr04a］，［Burr04b］）中使用的方法，通过考虑确定的DoD或者DoA的导向向量来处理多重散射。这种情况下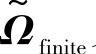，又是合乎DoD/DoA的排序需求的对角线矩阵。

类似式（6.20）定义了得到的MIMO信道相关矩阵，推导用于参考文献［Burr04a］，［Burr04b］中的有限散射模型，以及它与Kronecker假设的关系。这表明，当平均衰落超过了不同的衰落实现（即固定DoD和DOA）时，有限散射体模型没有显示Kronecker结构。这实际上是DoD和DoA之间一一耦合的结果，这恰恰是与Kronecker分离假设相反的。这一结论即使在多重散射中也同样适用，正如参考文献［Burr03］中详细说明的，这确实可以通过有限散射模型进行说明。然而，除非在DoD和DoA耦合之间有一个非常大数目的散射，有限散射模型才能表现为不可分结构。

2.虚拟信道的代表

在波束空间中，利用预定义的导向向量（见参考文献［Saye02］），使用虚拟信道表达式模拟MIMO信道，表达如下

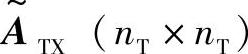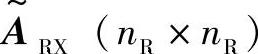使用单响应和导向矩阵和，nR×n_T的矩阵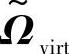是功率耦合矩阵Ω_virt的每个元素二次方根后得到的，此功率耦合矩阵的正实值元素w_virt，ij决定第i个虚拟发射角和第j虚拟接收角之间的平均耦合功率。通过与参考文献［Burr03］中的有限散射模型不同，矩阵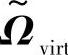不是对角阵。

注意，虚拟通道的表达值与虚拟方向是线性相关的，并且它的性质只取决于耦合矩阵。在选择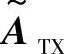和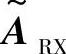时是有一定自由度的。尤其是当一个导向方向可以自由选择的时候，其余的方向则都是正交的。尽管与有限散射模型有相似之处，但是虚拟信道的角分辨率以及其准确性还是要取决于虚拟信道中的许多因素。后者不能任意选择，因为它与实际的天线配置相关。

3.Weichselberger模型

相较于以前的模型，Weichselberger模型用在特征空间域上而不是波束域上。处理MIMO信道是最初的想法是要放宽Kronecker模式可分性的限制，并允许发射和接收特征域之间能任意耦合。

介绍接收和发送相关矩阵特征值分解(www.daowen.com)

R_RX=U_RXΛ_RXU^H_RX，

R_TX=U_TXΛ_TXU^H_TX （6.28）

假设发送和接收之间的特征模式是互不相关的，Weichselberger（见参考文献［WHÖB03］，［Weic03］）提出了以下信道模型

式中H_w是一个n_R×n_T的独立同分布复高斯随机衰落矩阵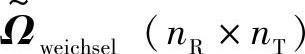，是功率耦合矩阵Ω_weichsel元素平方根矩阵，其正实值ω_{weichsel，ij}决定了第i个发射本征与第j个接收本征之间的平均功率耦合。

Weichselberger模型从根本上做了简化，它忽略了MIMO信道的空间结构，并且通过两端连接耦合矩阵的方法来描述MIMO信道。因此，发射机和接收机的相关特性是模拟联合的。此模型将Kronecker模型作为特殊情况（见参考文献［WHÖB03］，［Weic03］）。Weichselberger模型参数是接收和发送相关矩阵和耦合矩阵的本征域值。参考文献［BuHe03］概述中提及在特征向量和多径方向上有内在的联系。

注意这种模型也可以视为是基于相关性的。

4.用于锁孔信道的Gesbert模型

所有服从复高斯衰落统计的模型，比如上面提到那些，都不能再现锁孔现象，即使天线平均有很低的相关性，它们的信道矩阵都不是满秩的。这在参考文献［Sibi01］，［CLWV03］，［GeBP02］中进行了理论推导，并且在参考文献［AlTM03b］中进行了实验论证。

锁孔信道能够通过用一个不是满秩的矩阵代替独立同分布的复高斯衰落矩阵来模拟实现，

式中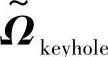，表示散射相关矩阵，即TX附近的散射体到RX附近的散射体的传播，且其他两个矩阵式独立同分布的随机矩阵。

这就有两个重要结论:振幅统计不再是复高斯的，所以第二特征就不够充分了;在不影响连接两端边缘的相关矩阵下，瞬时信道矩阵的秩受到散射相关矩阵秩的限制。利用MIMO信道分布系数的验证法已经用到真正的锁孔信道（见参考文献［AlTM03b］）第一次测量中，结果显示锁孔信道是双瑞利分布，正如式（6.30）所推。