基于相关性的模型描述了每对接收和发射天线之间的（复杂）相关特性。由于相关性取决于实际使用的天线配置，这些模型可以简单地类推到其他配置，除非计算新的相关系数。然而，由于这种相关性在模型中是确定的，所以在分析相关性对任何性能参数的影响时，这些模型是特别有用的。

1.基于全协方差的模式

如果是零均值高斯复杂圆形对称信道，则协方差矩阵（在这种情况下相当于相关矩阵）是足够说明MIMO信道统计特性的。

R_full=E｛vec（H）·vec（H）^H｝ （6.20）

式中，vec（·）是将列向量转成矢量形式;（·）H是求共轭矩阵;E｛·｝是求期望。

从式（6.20）可知任何信道的实现都可以由全协方差矩阵模型得出。

vec（H_full）=R_f¹_u^/_l²_l·vec（H_w） （6.21）

式中，H_w是一个有着统一方差，循环对称复高斯项的n_R×n_T独立同分布随机衰落矩阵;（·）1/2代表矩阵的二次方根。

在这一步，应该记住，当信道矩阵的实体是零均值高斯时，二阶统计数据只是一个充分而有效的信道统计行为的描述。对于式（6.20）的非高斯信道统计特性计算方式的修改我们将在后面讨论。

因此式（6.20）是对于循环对称高斯信道最普遍的描述。然而，它需要知道整个协方差矩阵的特征，其元素数量也随着数组大小迅速增长，另外并不是R_full的所有成分都有直接的物理描述。最后，式（6.21）的vec运算也是不易计算的。基于这些原因，一些模型已经基于许多假设的基础上来简化式（6.21），这些假设或者取决于发散和接收相关性质间的分离，或者取决于在一个波束-/特征空间里的分解。

2.Kronecker模型(www.daowen.com)

该Kronecker模型是在参考文献［SFGK00］和［ChKT98］中介绍的，并且在EU-IST SATURN（Smart Antenna Technology in Universal bRoadband wireless Networks）的项目中使用，通过使用一个可分离假设，简化全协方差的表达式。

式中，表示Kronecker乘积;tr｛·｝表示矩阵的迹;R_TX表示发射相关矩阵（n_T×n_T），R_TX=E｛（H^HH）^T｝;R_RX表示接收相关矩阵（n_R×n_R），R_RX=E｛HH^H｝。

将式（6.22）带入式（6.21），Kronecker信道矩阵变为

式中，（·）^T表示转置。

除了简化分析方式或者MIMO系统的仿真，式（6.23）还允许在TX、RX的最优化独立阵列，这也是这种模型广泛使用的原因。但是，必须明白的是，式（6.22）暗含着DoD和DoA之间统计独立的条件。因此，该模型的主要缺点在于它本身的主要假设，即它只建模了可分的联合角功率谱（见参考文献［BöHW03］）。因此所有的发射特征向量都与接收特征向量耦合，在相同配置条件下，反之亦然。就TX、RX方向而言，也是这样的。

3.对角相关信道

一些特殊的信道不能使用式（6.23），例如所谓的对角相关的信道，当天线的相关性（RX和TX）或者R_full所选择的交叉或对角相关性（不是天线相关性的相关）的值是0，并且其余的相关性都是单位幅度的时候就形成对角相关信道。例如在一个2×2MIMO的瑞利衰落信道，全相关的矩阵绝对值如

其中｜·｜指明了矩阵的元素单元的绝对值。

这种信道在参考文献［ÖzOe05］中提出，表现出了有趣的现象，例如达到最大化的信道遍历容量（大于独立同分布信道容量）。在参考文献［ÖzOe05］中的确提到，一个n×n的对角线信道的遍历能力计算如下:

式中，E₁（z）是对于n=1时满足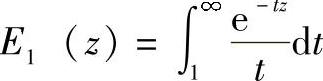的E_n函数。在式（6.25），容量的增大与天线的数目成精确的线性关系，而独立同分布的信道中容量则是渐进地以n增长。