MIMO技术是众所周知的，它允许除接收端外发射端的多样性。但是，在大多数研究中，考虑的是理想的各向同性的天线，而天线元素间的互相耦合被认为是对分集有很明显的影响。为了这个目的COST 273进行了几个工作，目的是评估这种相互耦合对MIMO无线信道容量的影响。

Tran和Sibille在参考文献［TrSi02］中第一次分开空间相关性和相互耦合，目的是分析它们各自对窄带信道容量的影响。定义了一些由2个、3个和4个单极天线组成的实数和虚数的圆形阵列类型来实现这个目的。一个真正的阵列包括这两个现象。虚数阵列只把重点放在空间相关性上，而重新耦合的相隔比较远的天线的阵列重点在相互耦合上。在角度是全方向的情况下，空间相关性可以用0阶J₀（2πd/λ）的贝塞尔函数量化，d是两个天线之间的距离。使用虚数阵列的信道容量似乎和这个量成反比，只有当相互阻抗Z₂₁是实数，相互耦合才使信道容量下降。本文在实数阵列中同样研究了负载阻抗的作用，如图5.19所示。如果是高负载阻抗，它的容量与使用虚数阵列的容量相当（没有耦合的影响）。如果是小负载，它的容量降低和使用距离较远天线组成的阵列和重新耦合造成的容量降低相似。一个主要结论是相互耦合和空间相关都不利于信道容量，但是两者都存在则导致了高容量。实数阵列的平均容量总是大于或者等于虚数阵列的容量。

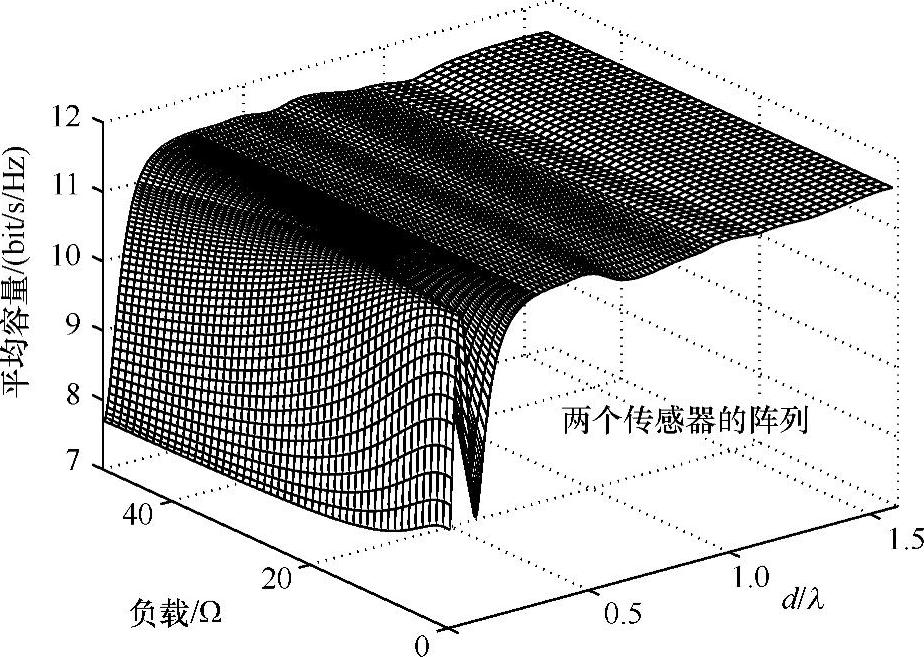
图5.19 负载阻抗和天线间隔的影响（见参考文献［TrSi02］）

为了进一步理解这些现象，稍后的工作（见参考文献［TrSi02］）使用几个人工阵列的变体来计算仿真的平均容量。这些变体包括人工辐射图样［尺寸耦合阵列（MCA），其中只考虑了真的阵列辐射图样的幅度，和相位耦合阵列（PCA），其中只考虑了真的辐射图样的相位］。图5.20绘出了一些结果，对小阵列天线来说，辐射场的相位在MIMO分集中比它们的大小更重要。

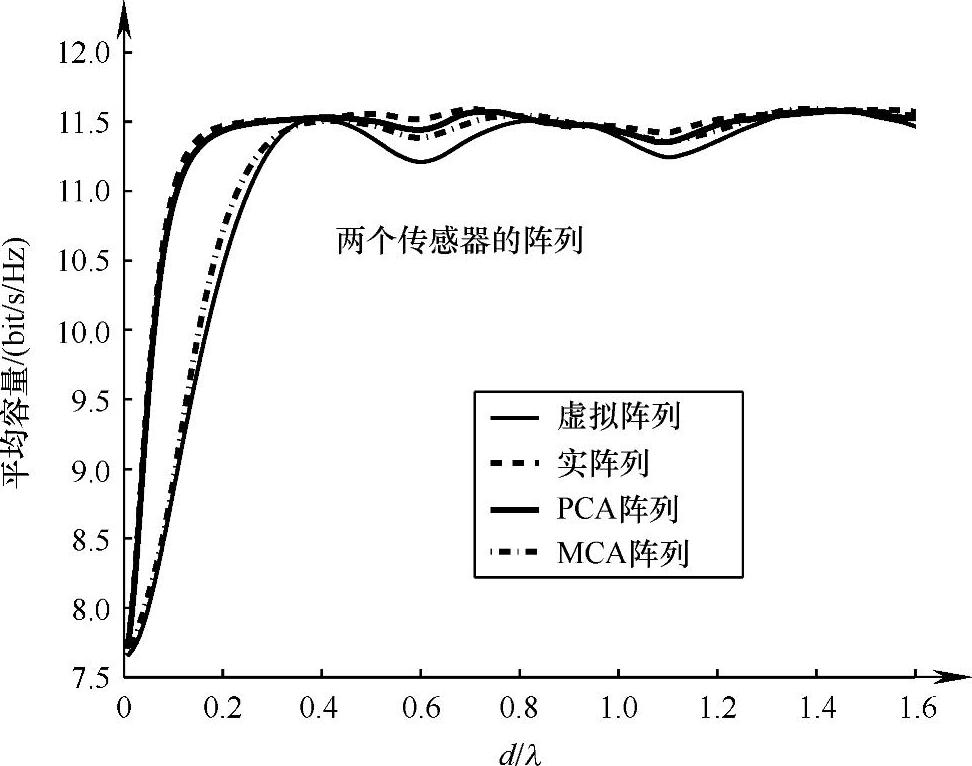
图5.20 信道容量中的幅度和相位的角色（见参考文献［TrSi03］）

参考文献［NdHH04a］中引入了基于电磁场的一个MIMO信道模型。使用的天线是在共振频率下的半波长偶极子。耦合是通过（M+N）×（M+N）的阻抗矩阵Z解释，与所有链路两端的电压和电流相关，M和N分别代表发送端和接收端的天线的数量。Z分解成A、B、C、D的子矩阵，其中A和D分别是发送端和接收端的互阻抗矩阵，而B和C是信道转移阻抗矩阵其中C=BT。问题是以积分方程的形式给出的，然后用MoM解决。用电压转移矩阵T来进行容量计算。使用两径信道模型（视距和地面反射），多数情况下能找到矩阵T^H的非零特征值。将一些结果与模拟的转移阻抗矩阵B的同一的独立高斯分布进行比较。图5.21表明了当考虑一个2×2MIMO系统的相互耦合提升时，即意味着信道容量的降低，T（2，1）和T（2，2）之间的相关性会提升。

图5.21 发送机和接收机阵列不同的元素间距下的T（2，1）和T（2，2）之间的相关性（见参考文献［NdHH04a］）

沿着同样的路线，具有耦合的信道矩阵H_c是用没有耦合的信道矩阵H_nc和两个在两边的耦合矩阵K_TX和K_RX表示的，用自我耦合归一化（见参考文献［NdHH04b］）。在4个方面扩展这个表达结果，一个与非耦合信道相应，另外两个是耦合只出现在链路的一端，最后一个是全耦合。(www.daowen.com)

容量是在高信噪比（20dB）的背景下，用信道矩阵H的相关矩阵R_H计算出来的。R_H也可以用R_H，nc表达，这个相关矩阵不包含耦合。耦合和非耦合两种情况下的容量差ΔC与耦合矩阵的特征值的基2对数的和近似相等。使用的信道模型是相同的独立分布的矩阵项，一般情况下天线是半波偶极子。使用了3种不同的信道矩阵的归一化:第一种，归一化H_nc，推导出H_c;第二种，直接归一化H_c来去掉因为耦合增高的功率;第三种归一化只取消了发送端的功率变化。随着发送端达到d_TX/λ=0.5的天线间距，会因为空间相关导致信道矩阵秩的减小。同样，降低天线间距可以提高发送端或者接收端的功率，也会带来容量的提升。总之，MIMO天线设计中需要考虑这两种影响的折中。

在所有这些以前的阐释工作中，Burr（见参考文［Burr04］）研究了相互耦合的影响和接收模式Ψ_R天线元素图样的转向矢量，和一个有限散射信道模型下的相关矩R，使用基于Steyskal（见参考文献［StHe90］）模型的相互耦矩阵C。在图5.22中，绘出了一个8×8天线系统的信道容量的CDF。我们看到相位耦合（C为正）提高了容量，反相位耦合（C为负）降低了容量和阵列的增益（因为耦合导致SNR的提高，带来更多的接收功率）。没有阵列增益时，其结果是相反的，这样阵列增益的影响似乎比提高相关性的影响更为明显。

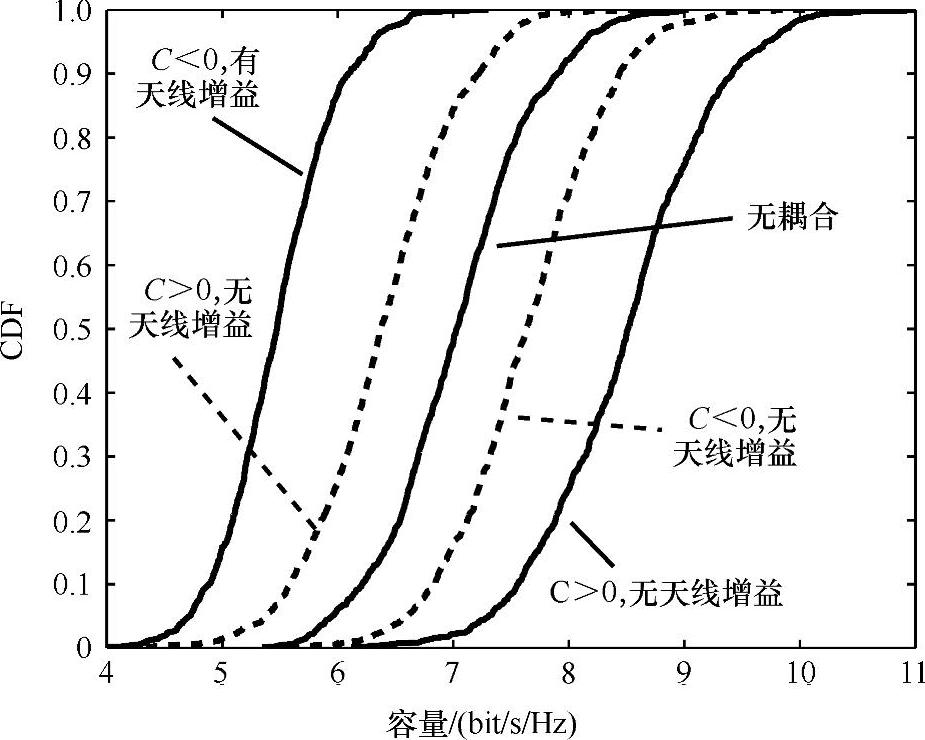
图5.22 一个8×8MIMO系统的MIMO容量的CDF（见参考文献［Burr04］）

相关矩阵R_R，ik项上的元素定向响应也被用来分析定义平均角度功率谱密度进行了分析（Angular Power Density Spectrum，APDS）。如果APDS是均匀的且所有天线是全向天线，则一类0阶贝塞尔函数是平均相关的，MIMO系统中可以用两种方法考虑耦合，一种是考虑修订的转向矢量和单独的元素样式，另一种是计算/测量阵列中的元素的直接响应。

Derneryd在参考文献［DeKr04］中分析了两个偶极子阵列的相关系数对分集特点的影响。这个系数用近场或者远场或者两者的参数计算，会得到相同的结果。相互耦合考虑了端口终止（50Ω）和以加权因子S（Ω）（即角功率谱）模拟的传播环境。图5.23给出了由两个远场辐射模式计算出的相关，其中入射波分布在90°的扇区内，左边的是天线间隔沿水平变化，右边的是垂直变化。在近场方法中，S（Ω）的相等，相关性是由天线终端的电压和电流得来的。

使用近场和远场参数，首先计算开关电路的相关矩阵E_{［VocVHoc］}，和电压的相关矩阵E_［VV^H_］还有推导出的端口终止条件。四天线配置中需要低相关系数和高天线效率之间的变换。

为实际中实现终端上MIMO阵列天线的分集工作的进一步进行，比如PDAs（见参考文献［RoHi04］），或者使用极化分集（见参考文献［WKSW03］）。更多的关于MIMO阵列天线的结果在本书的6.4节里给出。

图5.23 两个平行/垂直间距为波长整数倍的偶极子的相关系数的大小（见参考文献［DeKr04］;箭头代表阵列，月牙代表这个情况的角度分布）