一些大的测量活动是在传输场景或环境或频带的对照的情况下进行的。其他的文献想要覆盖更多的稀有场景或主题。所有的文献都包含了移动无线电信道的时间扩散和角扩散数据，不是通过从它聚集的上下文中将数据移除来选择。因此将本章节分为几个小部分，环境和频带的分别比较，以建模为基础的特征描述，簇的特征，扩散的散射功率，假定的静态环境和特殊环境。

1.移动无线电环境之间的比较

一些COST 273的参与者报告了包括不同传输环境的大量的测量活动。这使得不同环境间相似性和区别的研究成为可能。Salous和Hinostroza在曼彻斯特，英国的7个室内和室外到室内的环境中实施了大量的测量活动，其环境包括健身房、实验室、楼层到楼层和建筑物到建筑物之间的链路（见参考文献［SaHi03］）。该测量是利用曼彻斯特理工大学专有的线性调频脉冲探测器在2.35GHz，频带宽度为300MHz的条件下进行的;规定的总的动态要好于40dB。从测量结果，可以断定路径损耗、功率延迟剖面、时延扩展和相干带宽。其中，相干带宽范围从20～250MHz，在延迟为800ms时RMS延迟扩展从25～150ns。对房间、大厅和楼层到楼层之间的链路来说，莱斯分布最适合时延扩展分布，对建筑物内部走廊的视距环境来说，对数正态分布最适合。作者注意到延迟扩展对限幅电平有明显的依赖性:只考虑强于瞬时最大振幅-20dB的多径分量，这时的时延扩展均值大约为27ns，当给定一个35dB的瞬时动态范围时，这个数值变为44ns（见参考文献［SaHi03］）。

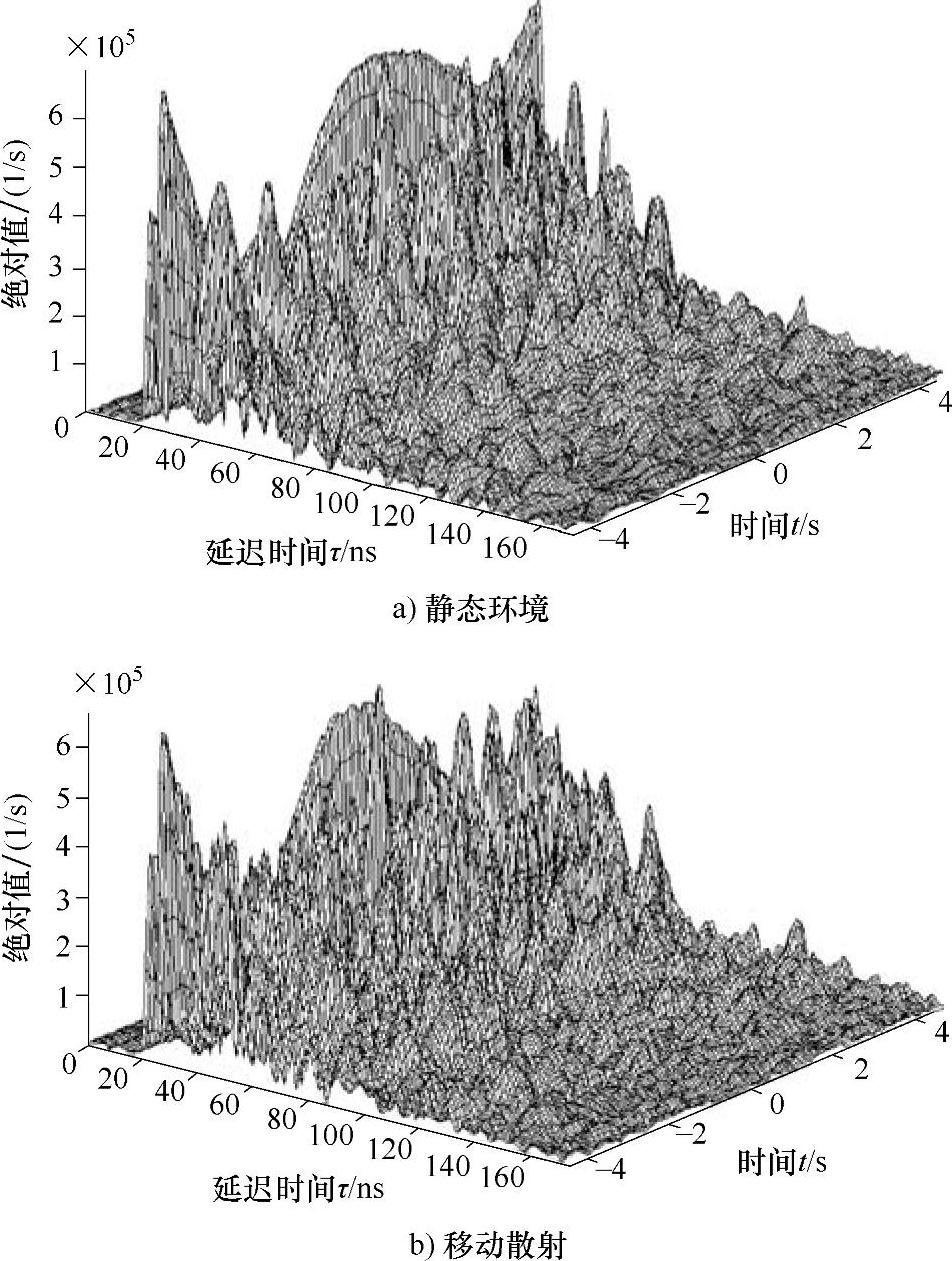
图4.39 在1.8GHz，移动天线下的时变脉冲响应（见参考文献［KaFr01］）

在5.2GHz频段，对在Lund、Sweden、Wyne等的室外-室内环境的测量结果显示了小的分散数字（见参考文献［WAKE04］），尽管这能很好地符合测量设备的几何学，但对不同频带作用不大。面对TX的房间的RMS延迟扩展的均值为7～10ns，在反面的房间的RMS延迟扩展的均值为12～14ns，走廊之间的RMS延迟扩展的均值为8～12ns。到达角的扩展几乎不取决于接收机或发送机的位置（大约0.24π或14度），但是离开角的扩展明显取决于发射机的位置，从0.03～0.08π或1.6°～4.4°（见参考文献［WAKE04］）。

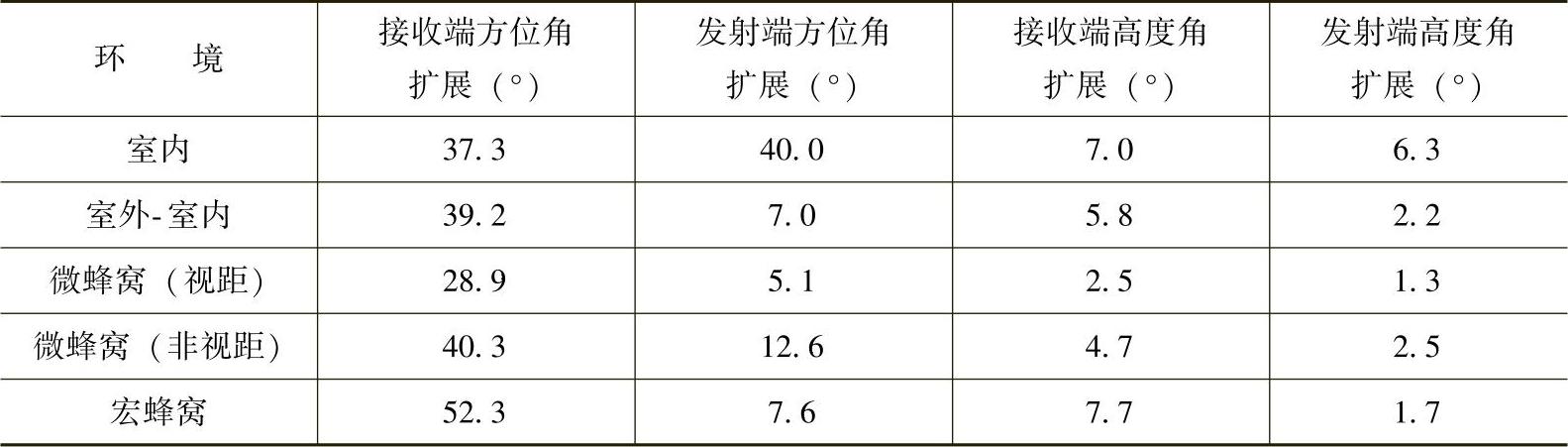
Kolmonen等对5.3GHz时的不同环境的扩展进行了比较（见参考文献［KKVV05］）。他们对典型的室内，室外-室内和微蜂窝以及宏蜂窝城市环境（Helsinki市中心）进行了大量的测量活动。对微型蜂窝环境，接收天线被放置的位置远远高于周围屋顶。作为一个快速并稳健的方法，可以利用双极化天线阵列，通过波束成形可以分别恢复接收端和发送端的方向信息。通过这个方法，可以根据3GGP TR25.966估计高度和方位角的角度扩展。首先，表4.10给出了个别环境下的角度扩展结果，这个结果显示了除了在室内环境下，发射端与接收端的结果在数值上可以相比较以外，发射端的角度扩展比接收端的要小。没有讨论天线操作的角方位的不同造成的影响。

表4.10 不同测量环境下的角扩展度（在参考文献［KKVV05］之后）

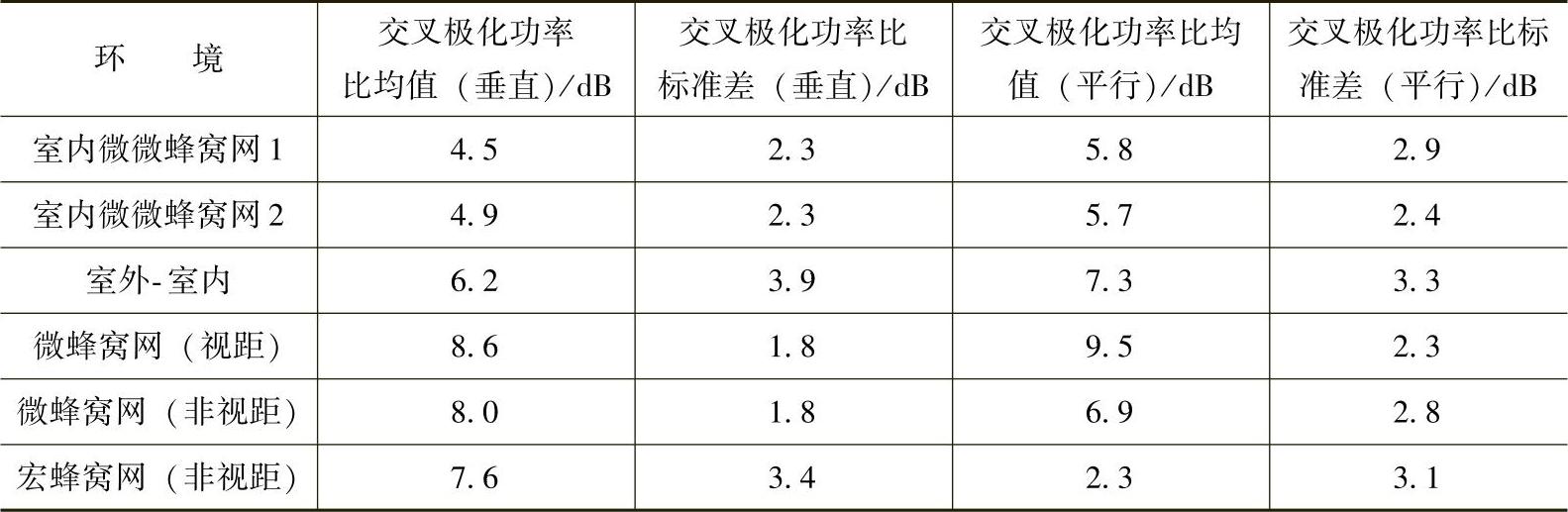
在非常相似的环境下，Kainulainen等在5.3GHz下做了一个大的极化调查，确定交叉极化功率比（XPR）以及同极性与相反极性链路之间的交叉相关系数。在所有环境中，交叉极化功率比大致服从对数正态分布，但是均值和标准差不同，见表4.11。对非视距链路，接收端和发射端的交叉相关系数很低，在0.26～0.45之间。在视距微蜂窝环境下，其范围为0.51～0.62，见表4.12。

表4.11 在5.3GHz时，不同环境下交叉极化功率比的均值和标准差 （在参考文献［KaVV05］之后）

同一地区的微蜂窝和宏蜂窝场景之间的区别是Hugl等调查的主题（见参考文献［HuKL02］）。他们在一个建筑物密集的城市环境中，有6～7层楼的赫尔辛基市中心，通过改变基站天线的高度来研究作为媒介的信道的平均到达角的影响。考虑到宏蜂窝或微蜂窝覆盖，基站天线高度为高于屋顶10m或在屋顶附近。20km的测量路径覆盖了在基站120°的扇区内，相当于1.5km的距离内的所有可以到达的街道。作者利用一个Bartlett波束成形来决定主导到达角并与几何到达角即发射机和接收机之间的直线角度相比较。对于宏蜂窝系统天线布置，主导到达角和几何到达角匹配得非常好，如图4.40所示。然而，对于微蜂窝系统装置，两者有很大的差距。作者认为这是由在屋顶上的传播和街道之间的传播的不同所引起的。向下倾斜的接收天线可以作为一个附加的因素纳入，以排除在基站下面的屋顶上的传播分量。

表4.12 在5.3GHz时，不同环境下交叉极化的交叉相关系数均值 （在参考文献［KaVV05］之后）

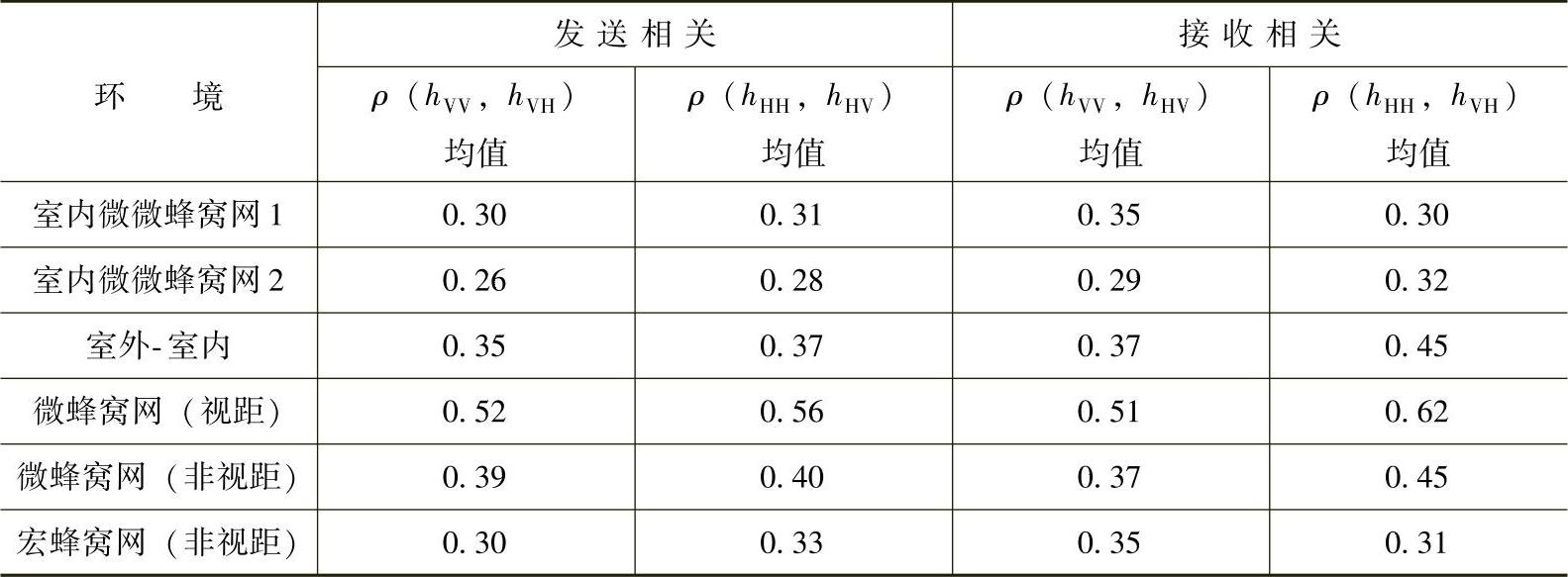
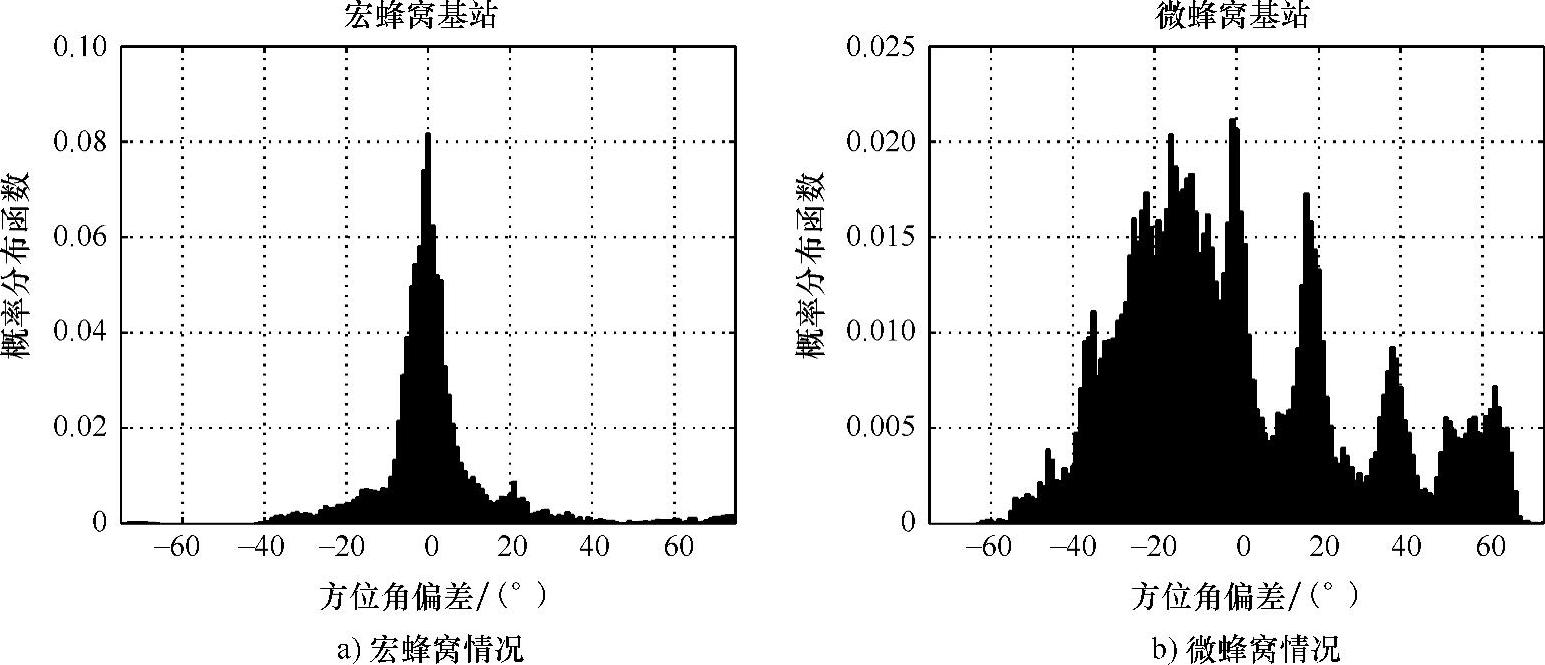
图4.40 主导到达角和几何到达角之间的偏差（在参考文献［HuKL02］之后）

2.频带色散依赖

对现有的系统带宽，一般假设统计信道特性的变化不会超过系统带宽。对于在不同波段上的运作，例如:UMTS FDD操作或多频带OFDM，以及对超宽带应用，这种不变性是不明确的。为了研究室内传播的频率相关性，Jämsä等测量了一个总带宽为10GHz，中心频率大约为6GHz的延迟扩展并与一些带宽为500MHz的子波段的结果相比较（见参考文献［JäHH04］）。同样，他把从10GHz上剪下的500MHz带宽的测量值的估计结果与在最大频率分解单独测量的500MHz测量值的估计结果相比较，用1601个频率点代替81个。全分辨率扫描显示了更高的动态范围，但是作者推断超宽带测量可以被用于窄带建模，通过利用不同次波段的相同数据可以得到附加的好处。关于频率依赖性，他们论述为除了信号强度对频带的强依赖性，没有发现关于频率的真实趋势。尽管，通常延迟扩展倾向于随频率的递增而递减，见表4.13。

表4.13 在一个空房间中，在视距和非视距的条件下，测量不同频带的室内RMS延迟扩展

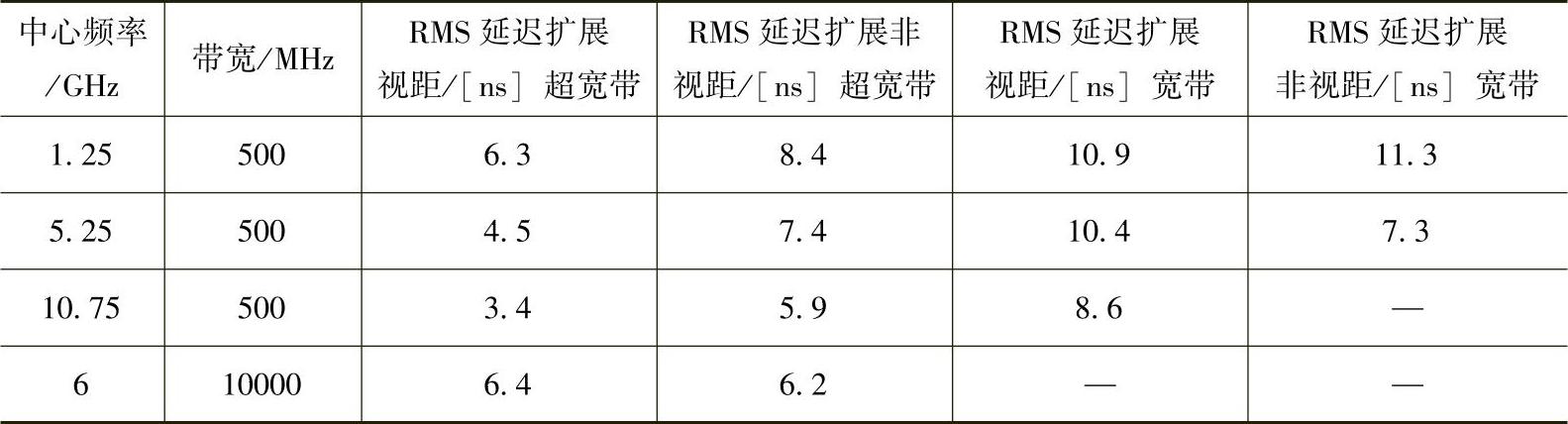
注:超宽带结果是从完整的10GHz范围切割的部分波段结果，宽带结果是在500MHz上单独扫描（在参考文献［JäHH04］之后）。

Liu等研究了在中心频率为6.85GHz，带宽为7.5GHz情况下的相似带宽的空间相关性。他们的目标是确定多频带OFDM（MB-OFDM）应用的实际天线间隔（见参考文献［LAME05］）。测量是在一个6×6m²的单独工作间里进行的。保证空间相关系数小于0.6的距离从4GHz时的2.2cm下降到10GHz的0.4cm，粗略地与频率成反比。就相关距离而言，LoS和NLoS之间的差别是次要的，其中，后者通过在接收端和发射端之间放置一个大的接地铝片来获得。

Bultitude和Schenk测量了在1.9GHz和5.8GHz，在曼哈顿电网和在渥太华市中心的以非视距传输为主要媒介的大城市的信道（见参考文献［Bult02a］，［SBAP02］）。测量值是在带宽为10MHz时，在一辆货车的顶部获得的，并且测量中货车运动的距离达1km。为了能够分开平行街道和垂直街道，数据分析是根据每条街道做的。Bultitude和Schenk发现在5.8GHz有一致的低延迟扩展（低16％）和大的相干带宽。在1.9GHz和5.8GHz延迟扩展均值分别为213ns和184ns。一致的单边相干带宽大约在1.8MHz和1.9MHz。他们将这个部分归于高频引起的高衍射损耗。在高频菲涅尔带同样很小，但是并不明确这是否能导致多径分量的更好的传播条件或较少的有效散射体（见参考文献［Bult02a］）。

Salous和Gokalp在曼彻斯特市中心（见参考文献［SaGo01］），Foo等在布里斯托尔市中心和郊外（见参考文献［FBKE02］）分别调查了城市环境下UMTS FDD双工带之间的差异。Salous和Gokalp利用UMIST的专用信道探测器分别在中心频率为1950MHz和2140MHz的两个60MHz的频带同时对行人和车辆的信道分别测量其UMTS的上行链路和下行链路。对照2个频带以及60MHz频带中5MHz子频带的测量结果，作者注意到子频带或频带间的频率依赖偏差是由信道的偏离量所决定的。对于延迟扩展结果，在NLoS中比在LoS环境中子带宽的方差要大，上行链路和下行链路的差距在稠密散射的环境中要比在稀疏散射的环境中大。注意到子频带或频带之间的频差比混合数据文件表面上的要大。大概因为在这些情况下色散是最强的，这些偏差在最大范围或最小链路预算时是最大的（见参考文献［SaGo01］）。

后一个结论同样是Foo等得到的（见参考文献［FBKE02］）。在这种情况下，以1920MHz和2120MHz为中心频率的两个20MHz频带同时通过一个移动车辆测量。利用一个2维一元ESPRIT算法估计到达时间、到达角度和多径分量的功率。当对照两个频带时可以在时间和角度上看到不同的响应。两个环境和两个频带之间最大的不同是（方位角）角扩散，两个频带之间有强的解相关。在城市环境中比在郊区中更富有散射，从大的角扩展测得城市环境的解相关非常强。作者从他们的发现中推断在散射非常多的环境中基于上行链路测量的下行波束成形是次优化的（见参考文献［FBKE02］）。

3.以模型为基础的特征描述

最一般的描述移动无线电环境的方法是通过测量值。然而，对简单的用户场景和简单的建造环境，分析模型仍然可以提供对基本现象的洞察。Hansen估计1m³的房间的功率延迟剖面以建模短距离通信，正如在WLAN或Ad-Hoc网络中的应用（见参考文献［Hans03］）。基于射线追踪理论，并假设极化充分混合、传输方差均匀分布、散射路径随机分布，得到了立方体的具有exp（-τ/στ）形状的功率延迟剖面:

σ_t=（2dξτ）-1（4.23）

反过来，d=-ln（d_E），其中，d_E为反射衰减均值，ξτ代表房间大小，用每单位时间墙壁之间相互作用的次数表示。关于指数式衰减，στ等于延迟扩展。Hansen以为延迟扩展是关于建模不精确度的一个强健的参量，并以为因此导出的模型是一个对许多传播场景好的近似。他将他的模型与在5.25GHz，带宽100MHz的情况下，在一个办公室环境的房间或走廊中的测量值相比较。测量的RMS时延扩展值很小，在7～13ns之间。所得的解析值完全可以作为上界，因为这些值通常超出测量值一个标准差或更多（见参考文献［Hans03］）。

与Hansen的方法相对照，因为大多数的现实环境都太复杂，不能利用解析信道模型，Fügen等致力于改进仿真工具（见参考文献［FMDW03］）。他们在没有高建筑物的卡尔斯鲁厄市的宏蜂窝环境中超过大约500×700m²的区域，利用卡尔斯鲁厄大学专有的三维射线跟踪工具仿真。仿真包含了多径反射，多径衍射以及两者的结合。基站放置在25.5m的高度，远高于建筑物高度的平均水平12.5m，载波频率为2GHz。结果显示MT端的角扩散在街道交叉比在街道之间要高很多。同样，作者在MT端和基站建模了延迟和角度扩展，与一个基站和MT之间的距离的负指数函数相抵消。缺点是建模的延迟扩展随距离下降。

4.簇内色散

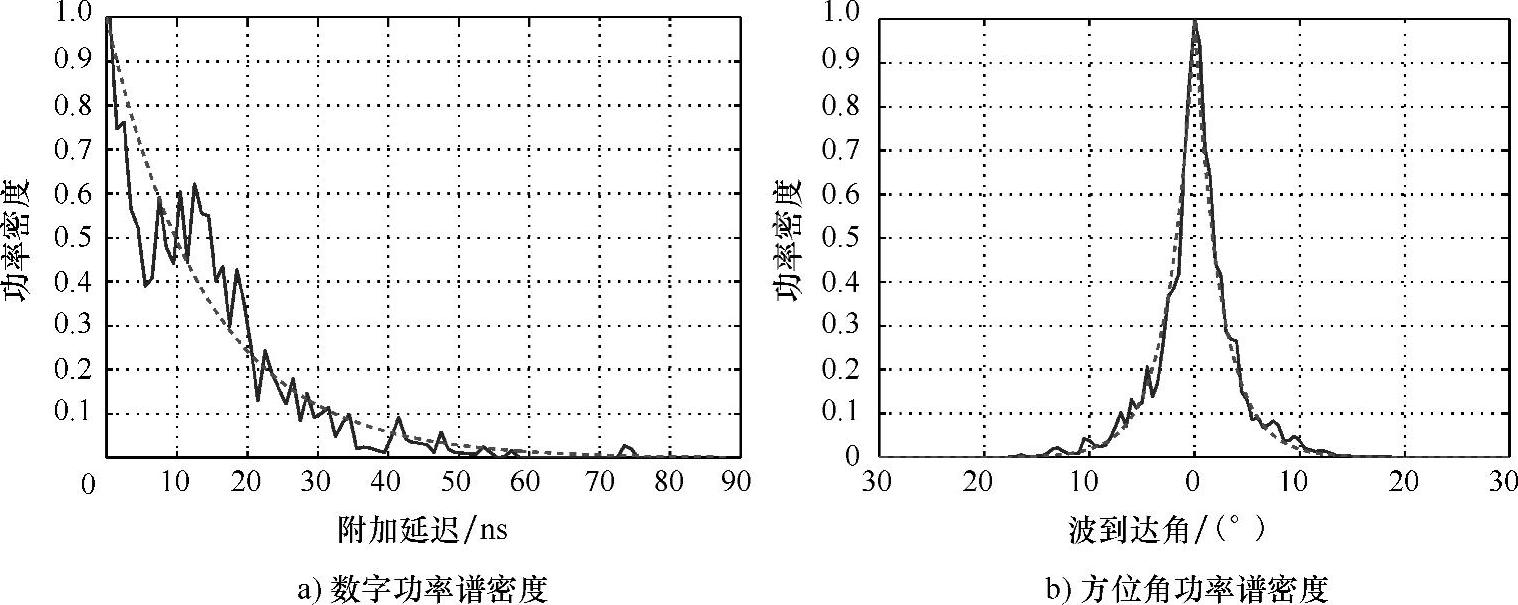
第6.8节提出的散射体簇的概念已经纳入无线信道建模，用于缓和和改善移动信道特性的统计性描述。在这个概念中散射环境被看作是由散射体集中度的分布式集合所组成的。散射物体的这些簇的特性的描述是由COST 273中的若干分组承担的。Chong等人在5.2GHz，带宽120MHz的情况下，在一个大的办公室和空地上在办公时间进行了测量。利用一个用于估计多径分量的FD-SAGE，通过一个2维高斯核密度估计器聚合时延-方位角估计值;一个簇被定义为一组具有相似附加时延和到达角的多径分量。Chong等人提出了一个簇模型，这将在MIMO建模的章节中讨论，在这个模型中时域和空间域对阻碍视距（Obstructed Line-of-Sight，OLoS）和非视距（NLoS）链路是独立的，但对视距链路是耦合的。对视距链路，簇内的边缘功率密度分布是具有附加延迟的指数式衰减，也是方位角功率密度的拉普拉斯算子，如图4.41所示。

(www.daowen.com)

图4.41 视距环境下的簇内的边缘功率密度分布，测量出的（实线）与建模得到的（虚线）的比较（在参考文献［CTLM02］之后）

Czink和Yin提出了一种替代方法，利用Bartlett波束成形在到达角-离开角域来粗糙地确定簇。相应到达角和离开角的SAGE估计来源于瞬时信道实现，并将利用这个簇信息进行选择（见参考文献［CzYi05］）。从簇估计中，可以计算角度扩展。从综合资料上看，扩展估计结果几乎是合理无误的。作者认为接收端和发射端的簇内角度扩展的测量数据不同（见参考文献［CBYF05］），很可能是由于走廊中发射天线的位置，如图4.42所示。这种方法是对早期基于固有信道的到达角-离开角估计值尝试的一种改进（见参考文献［CHÖB04］），这种尝试一致的低估了簇扩散。

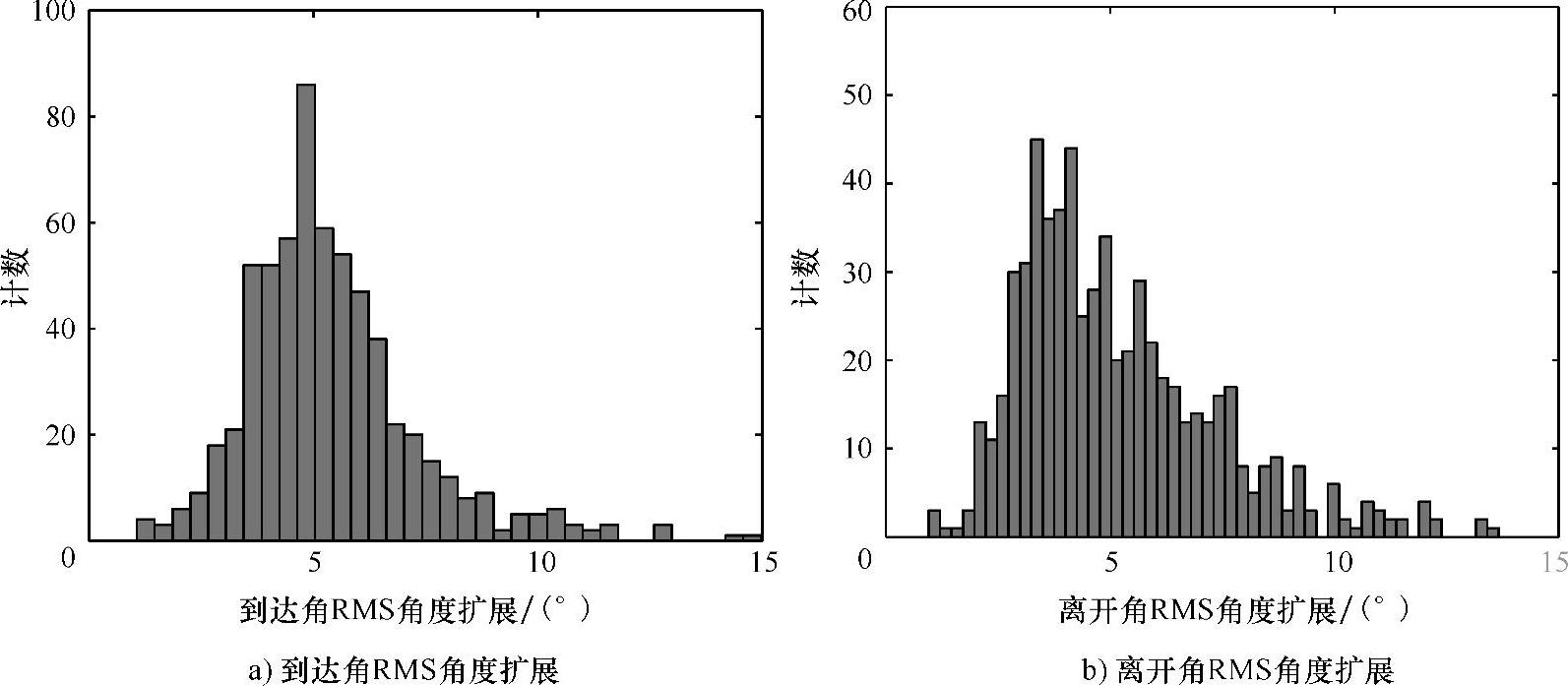
图4.42 对室内测量数据估计的簇角度扩展的直方图（在参考文献［CBYF05］之后）

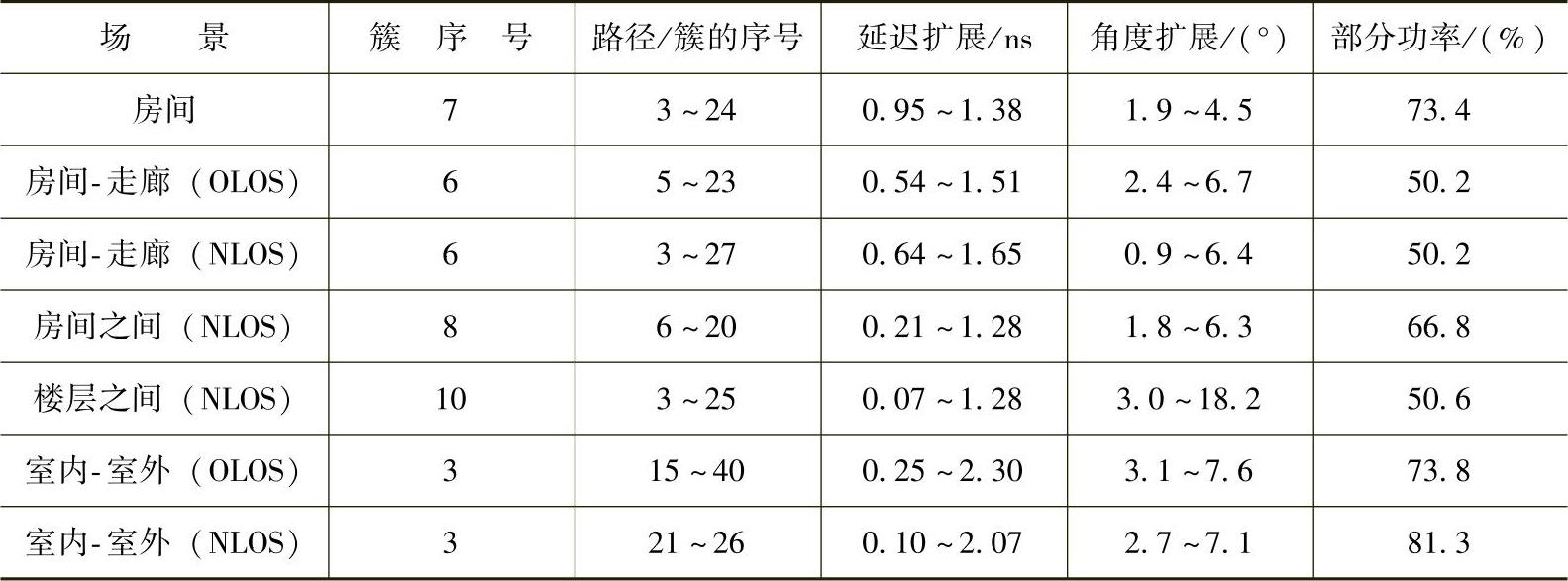
在从3.1～10.6GHz的超宽带，在一个木制的日本居住房屋内，Haneda等同样确定了簇特性。利用SAGE算法提取了总共100条路径，联合检测延迟-到达角（方位角）。结果在表4.14中给出，并比上面用文件证明的结果要低，这可能是由于短路径、轻型结构和相对小的建筑物大小的原因。表4.14最后一列的记录指的是可以由SAGE算法恢复的功率大小，这表明大约有1/4～1/2的功率不能被模拟。

表4.14 居住环境的UWB簇特性（在参考文献［HaTK05］以后）

5.漫散射功率

在移动传播环境中的漫散射功率的大小问题仍然在很大程度上未得到解决。这对高分辨率参量估计应用有重要意义，从MIMO容量的观点看，一般假设为一个离散的散射体模型。

Degli-Esposti等人在城市环境中，通过从检查建模方面到漫散射分量确定延迟和角度扩展的范围来处理这个问题（见参考文献［DSGK02］）。他们通过将测量结果与3维射线跟踪的结果相比较来实施这个方案。测量数据是在2154MHz的频率下，在赫尔辛基市中心，沿着水边，在高层建筑物之间得到的。射线跟踪算法的应用是基于一个完全的3维成像射线跟踪技术（见参考文献［DDFR94］）将有效粗糙度方法与漫散射相合并（见参考文献［Degl01］，［DFVG05a］）。方位角的角扩展预测报告在总体上是好的。延迟扩展预测同样很好;图4.43显示了一个准视距路径的测量结果。在这种情况下，作者推断对横跨港湾的远距离建筑物之间的漫散射建模可以帮助测量路径上延迟扩展分布的重建。但是，对大约10％的路径，模型运行结果不好，尤其是在基站在屋顶之上并且手机陷入高层城市环境中的时候。Degli-Esposti等人假定在这些情况下，建筑物数据库可能是错误的（见4.3节）并且/或者在射线跟踪中没有考虑足够多的建筑物，因此远距离散射体不再发挥作用（见参考文献［DSGK02］）。

Trautwein等人提出了一种分析大量测量值的方法（见参考文献［TLST05］）。他们利用早先Richter和Thomä提出的联合估计到达角、离开角、时延、多普勒和极化特性的Rimax估计算法量化了漫散射功率的大小（见参考文献［TLRT05a］），同样见4.4节。在从信道转移减去估计的相关信息后，算法利用延迟域用参数将误差引进噪声，并得到了一个指数衰减散射功率。假设这个功率包含了所有的漫反射多径分量（DiffuseMultipath Components，DMC）。环境之间有较大差异:在一个户外的小宏单元，反射功率与漫散射功率分量比值的中值是14dB，而在München的一个大的有金属支撑结构的铁路大厅反射功率与漫散射功率分量的比值是-10.3dB。表4.15给出了一些其他的环境（例如，城市微小区街道和广场、室内礼堂大厅以及公路桥微微小区）彼此之间的功率比。在具有数额较大的DMC功率的环境中与在具有相对较高的功率的环境中相比，估计器趋向于找到较少的反射分量。

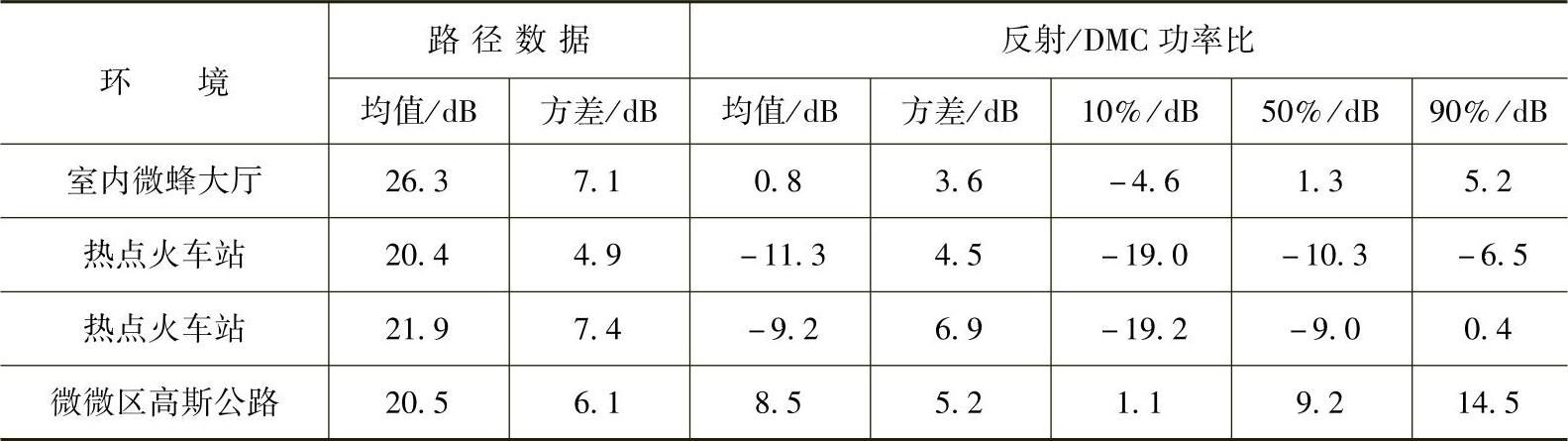
Trautwein等人的关于漫散射功率在一些环境中不能被忽略的观察报告同样在COST273中被其他人提到过，即他们的经验认为似乎存在一个关于可以被高分辨率估计器捕获的功率值上限。Wyne等人恢复一个室外-室内有40个多径分量环境下的功率，在最坏的情况下恢复了60％，平均恢复率在85％左右，最可能的提取率在90％左右（见参考文献［WAKE04］）。Haneda等人发现尽管他们强制地计算了100个反射分量，尽管在高时间分辨率的条件下（见参考文献［HaTK05］），在室内数据也要略微的低一点，在50％～80％之间，见表4.15。

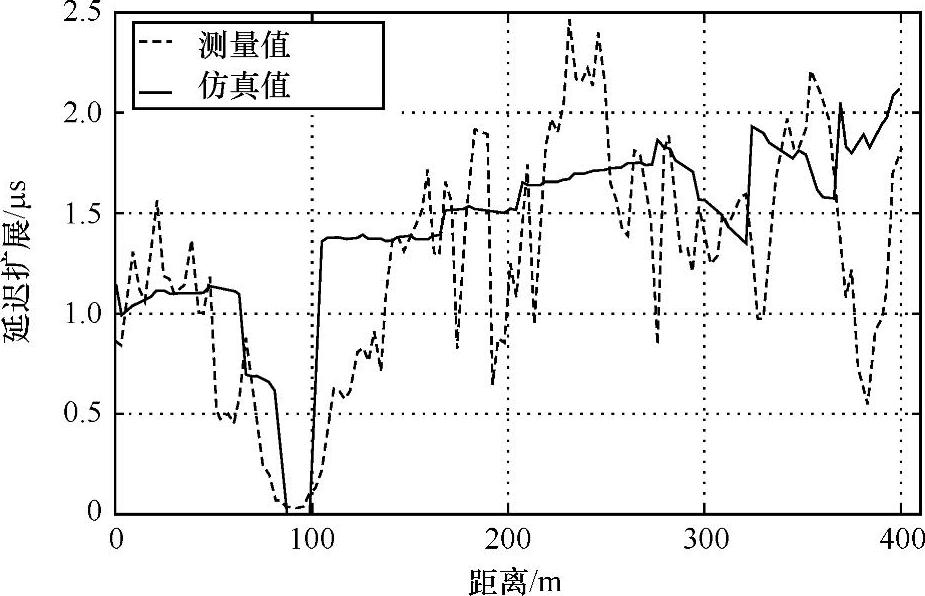
图4.43 延迟扩展的测量值和由射线追踪模拟得到的值的比较 （在参考文献［DSGK02］之后）

表4.15 路径的数据以及不同环境下的反射和散射分量功率比 （在参考文献［TLST05］之后）

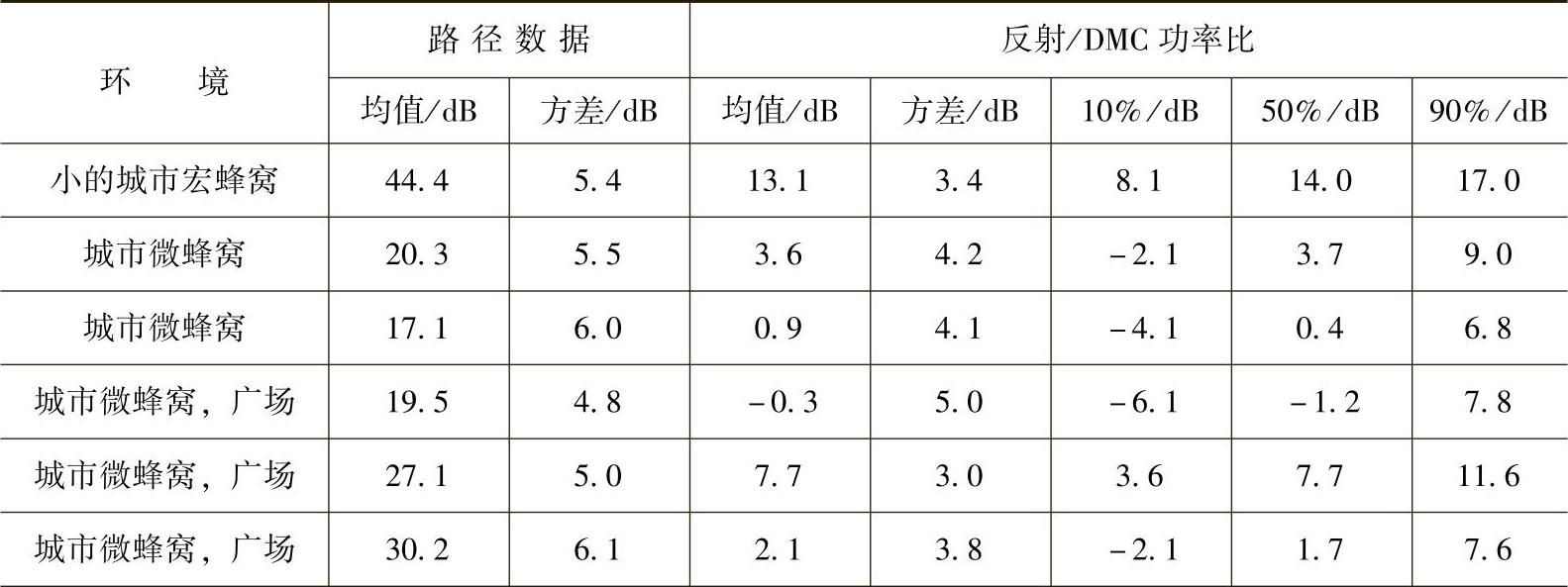
（续）

6.静态信道

Kattenbach和Früchting调查了移动散射体相对于移动接收天线的运动对信道的影响（见参考文献［KaFr01］）。为了这个目的，他们在3个不同的频段1.8GHz，5.2GHz和17.2GHz分别进行了测量，带宽为600MHz，为了达到好的时间分辨率，利用了一个专有的阶梯式的频率关联探测器。在房间中走动的人们担任移动的散射体，对静态信道的作用是很明显的。同样，在起源于例如建筑物的构造一部分的同样多的多径路径下，随时间变化的振幅变化显然要比相位波动明显，其中，建筑物是根本不变的。移动散射体的影响也明显地不同于接收机运动的时变信道的特性。因此，Kattenbach和Früchting推断有移动散射体的信道应该与那些由于接收机变化只显示时变特性的建模不同。对建模时间相关，移动散射体可以不考虑其数量而被忽略，但是当建模振幅和相位变化时不能忽略移动散射体的影响。作者在这3个测量频带上没有发现基本频率依赖性。

Medbo、Berg和Harrysson特别建模了在非视距无线局域网场景下，接收机不运动时的时间变化（见参考文献［MeBH04］）。整晚15h，在5.25GHz，频带宽度200MHz的情况下用一个矢量网络分析仪每5s扫描一次，得到了测量数据。看到的变化被认为是由于任意端的天线附近的人移动所引起的。终端机被放置在靠近走廊的一个房间中，基站/接入点在走廊上。他们用一个偏差参量p:总功率描述测量的转移变化，p作为时间间隔的函数，在测量的转移频谱的平均偏差中，均值决定了间隔在1000s以上，即，100个次测量值。总的接收功率本身显示了在超过15h的时间内非常恒定。在夜间，没有人在周围，p相对于总接收功率大约为-50dB;在白天，个别情况下高于-10dB，如图4.44所示。作者建议利用p作为一个非静态测量环境的指示器，例如在MIMO测量中（见参考文献［MeBH04］）。信道动态的2个不同起因是可以鉴别的，干扰并伴随低多普勒频移和干扰伴随高多普勒频移，最可能与站或坐在靠近任意一端天线处的人们有关，第二点是由于从旁边走过的人们。Medbo、Berg和Harrysson将变化建模为移动的人的影响，包括一个圆柱散射和一个简化为刀口衍射的阴影分量。参考文献［MeBH04］给出了测量值和模型之间良好的一致性报告。

Skentos等人检查了在视距传播条件下，在雅典的一条宽并且热闹的街上的静态房顶-街道场景（见参考文献［SKPC04］）。接收机在一个高10m的楼顶上，发射机在距地面1.9m的4个不同位置，发射机之间的距离为115～236m。载波频率为5.2GHz，带宽为120MHz，在两端都应用了8个元素的均匀线性阵列。这些数据是利用功率延迟剖面的一个功率相关测量标准，对广义平稳性的测试，在所有的64条SISO链路上取的平均值。关于测量时间的相关系数的门限被设置为0.75，所有的数据都通过了。时间色散的基准值是平均超过时延25ns，RMS时延扩展为42ns。测量信道随时间缓慢变化，观察到的多普勒最大的频移为大约1.5Hz。在屋顶放置的接收机比在街道上放置的发射机的角度色散要小。在方位角-延迟平面多径分量的簇集对发射机和接收机都是明显的，但是没有提取出任何簇参量（见参考文献［SKPC04］）。Skentos等人同样调查了屋顶-屋顶的链路，作为一个典型的固定无线接入场景。在这种情况下，发现色散很小，在载波频率为5.2GHz时最大多普勒频移为0.63Hz（见参考文献［SkCK05］）。

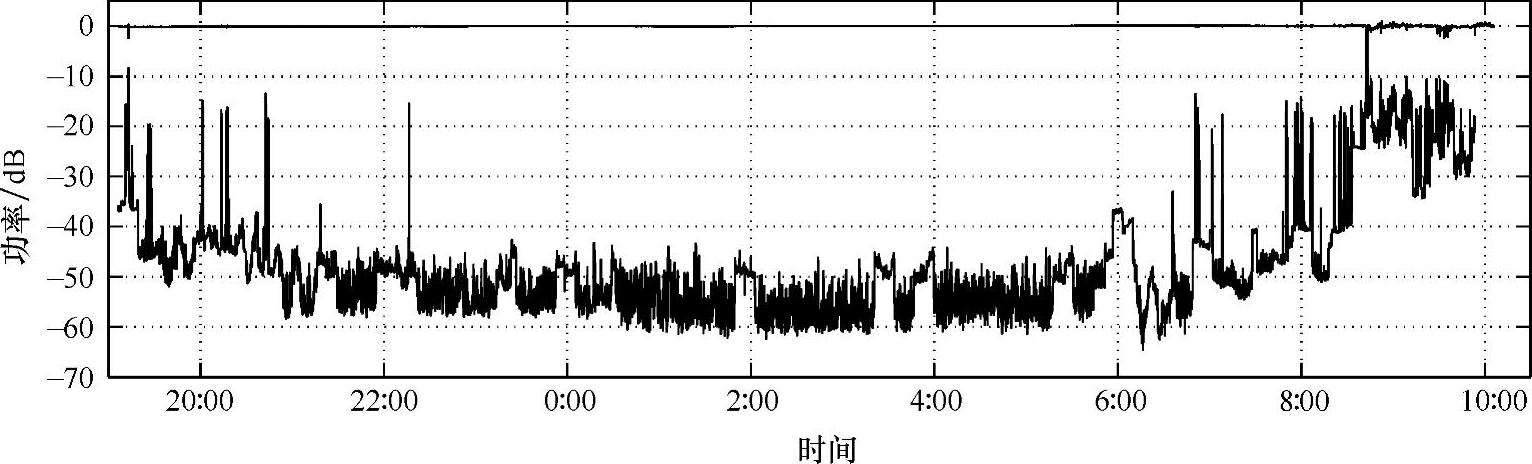
图4.44 在夜间的总宽带功率（上曲线）和时变功率（下曲线）（在参考文献［MeBH04］之后）

在静态环境下的另一个实验是由Marques等人实施的（见参考文献［MPKZ01］）。他们在1.7GHz，带宽为30MHz时，在杜伊斯堡，基站位于屋顶之上，MT在街道中静止，路径长度在20～320m之间时，确定了相关时间。在相关系数低于0.9时，在具有相同时间偏移的测量点平均来看，频率范围的相干性在相关系数低于0.9时便不存在。作者发现中值一致性的周期长度在4.3～6s之间，这取决于所在的位置。

7.特殊室外环境的特征描述

Kemp和Bryant应用蓝牙技术在2.4GHz的工业、科学和医学频带（ISM），在工业环境下调查了具有丰富散射的环境（见参考文献［KeBr05］）。路径长度因此相对较短，在一个石油化学工厂大约为20m，与多层建筑物并排的停车场大约为80m，在一个配电变压器站能达到250m。延迟扩展和误比特率是通过120000个片段决定的，这些片段的大多数来自石油化学工厂。正如这些设备与普通蓝牙器械相比有很高的传输功率，在处理过程中，脉冲响应可以被限制在30dB的瞬时动态范围内。石油化学工厂的平均延迟扩展是38ns，变电厂为88ns，停车场为76ns。在停车场的结果的变化比在其他环境高2个数量级。作者将这个归于两个明显不同的反射过程的存在，车之间的反射在附近，以米计量;建筑物之间的反射大约有100m远，以百米计量（见参考文献［KeBr05］）。

相比之下，在60GHz的室内环境应该会比较好建模，正如Geng等人（见参考文献［GKZV05］）报导的。从在赫尔辛基科技大学校园测得的方向图，他们推断在视距情况下，信道可以通过直接通路和一阶反射很好地描述。在非视距情况下，衍射是主要的传播机制。

在隧道的入口后面存在一种非静态传输条件下的特殊情况，Molina-García-Pardo等人调查了这种称为“激励区”（见参考文献［MaLD94］）的过渡结构，他们利用UTD射线跟踪检验一个横截面积为8.5×5.2m²（宽×高）的矩形直线隧道的前100m的路径损耗、延迟扩展和角扩展（见参考文献［MoRJL03］）。在2.1GHz，发射机放置在距离入口100m的隧道中心线上的3个不同的高度，相应的高度角为15°、30°和45°。在激发区，路径损耗、延迟扩展和角扩展激烈的变化。角扩展在激励区的开始达到最大变迁值，延迟扩展在最后达到，如图4.45所示。激励区的长度取决于发射机的高度角，正如扩展的最大变迁值一样:高度角越小，激励区越长，扩展的最大变迁值越小。

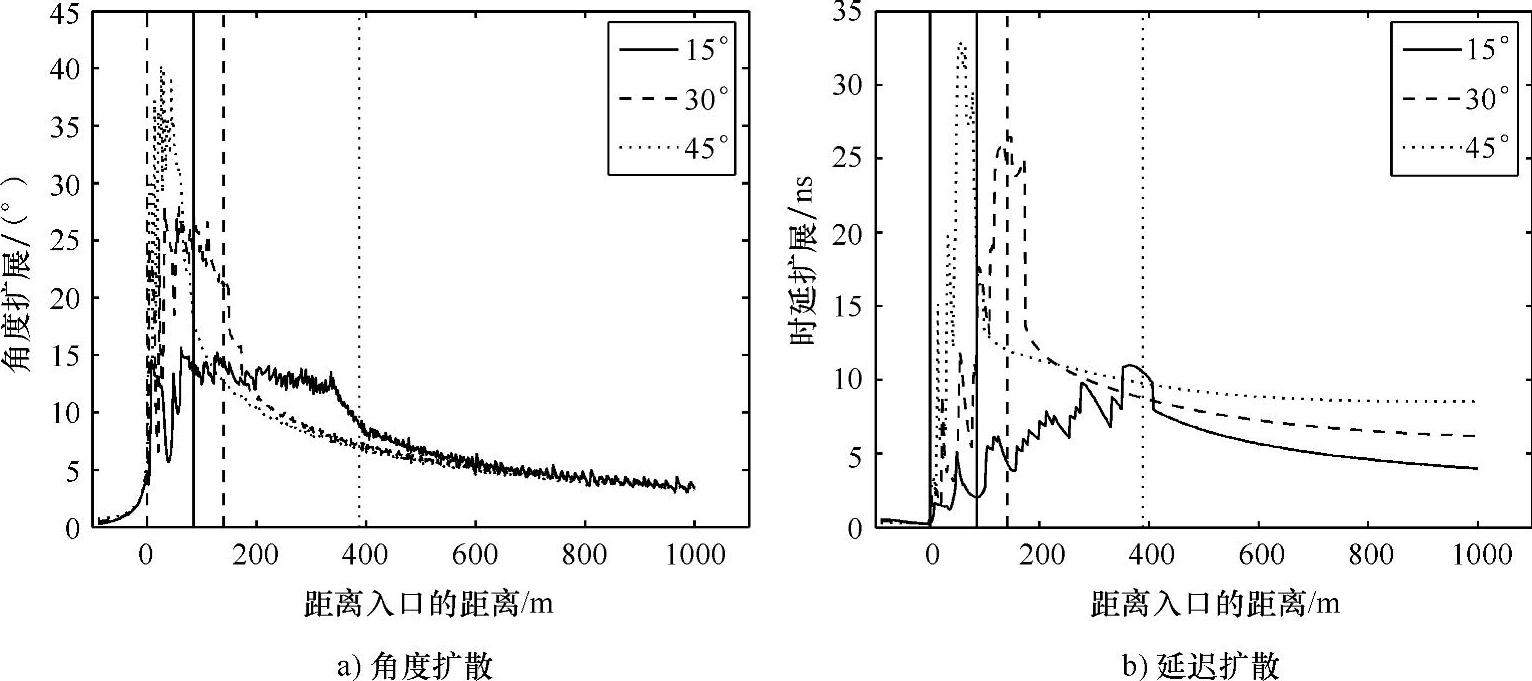
图4.45 在3个不同的发射机高度角:15°、30°和45°（实线、虚线、点线）下，隧道入口后面的激励区的角度和延迟扩展

注:隧道入口在0m处，垂直线表明各自激励区的终点（在参考文献［MoRJL03］之后）。