与窄带情况相反，宽带情况下，到达波的相对时延与信道中信息的基本单元（符号或比特）相比很大;因此，宽带信道通常通过一个信道脉冲响应建模，不同路径的数量是在窄带情况下得到的。

在视距的大多数情况下，第一条路径被建模为莱斯分布，因为这条路径包含了视距组件，所有其他的路径被建模为瑞利分布。这种方法已经在参考文献［Corr01］中提出过，第一条路径的莱斯因子是作为窄带莱斯因子、系统带宽、RMS延迟扩展的一个函数而导出的。然而，上述提出的莱斯因子只适合于信道脉冲响应的特定结构。

另外一种克服建模参量带宽依赖性的方法是利用时变转移函数代替时变脉冲响应，如此以至于窄带模型的所有已知性能可以被应用（见参考文献［Corr01］，［Katt02］）。

参考文献［CaCo02］提出了一种在宽带瑞利或莱斯环境下通过PDP描述其衰落深度的特征的时域技术。接收功率的PDF为

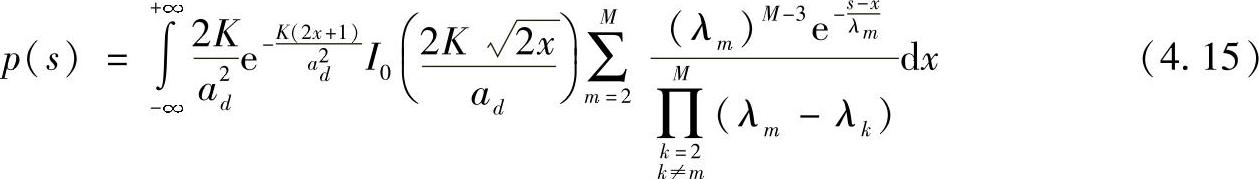
式中，a_d是视距路径的数量;K是莱斯因子;I₀是第一类零阶贝塞尔函数;λ_m是协方差矩阵的特征值，是通过生成一个矩阵得到的，其中矩阵的元素是通过不同频率分量、在传递设备中所用的滤波器的频率响应以及由系统带宽决定的增值带宽的相关函数乘积给出的。

当K趋于0时，与第一条路径相关的莱斯分布退化为瑞利分布，因此，与非视距情况相一致。

通过利用这个模型，不同信道模型的衰落深度可以被简单地估计为不同的PDP。当衰落深度被表示成莱斯因子、传输信道的系统带宽和RMS延迟扩展的乘积的函数时，可以得到如图4.37所示曲线图。

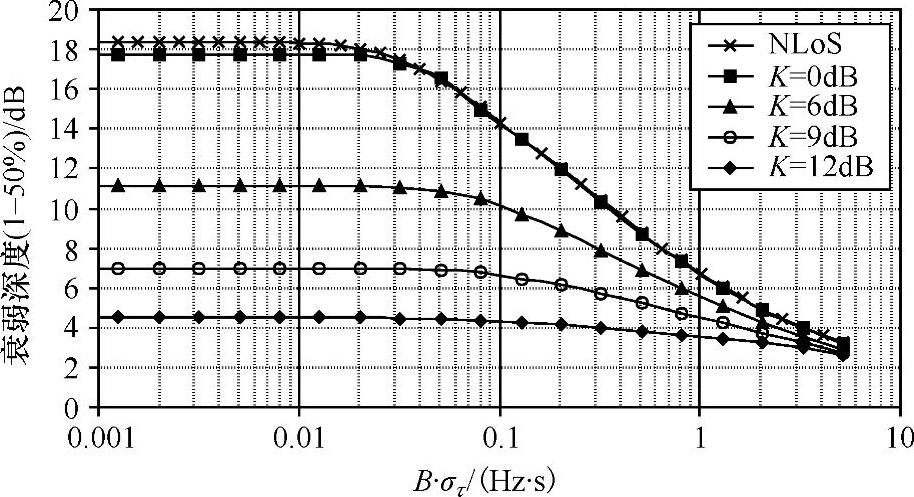
图4.37 衰落深度的指数模型（见参考文献［CaCo02］）

图4.37所示的结果与衰减率等于RMS延迟扩展倒数的连续指数式衰减函数相一致，因此代表了信道模型的一个大型集合，通用于模拟传输信道。正如观察到的，对K的任意值，在Bστ＜0.02Hz·s时衰落深度几乎保持不变。这与系统带宽低于传输信道相干带宽的情况相一致，其定义的频率相关性为90％（见参考文献［Rapp86］），因此，信号是在平坦频率环境下。在Bστ值较大时，衰落深度随系统带宽的增加而减小。

参考文献［CaCo01］提出了一种不同的基于环境性能的方法，它对不同到达分量之间的传播路径长度的偏差测量更加精确。提出的这种方法，说明了传输路径长度的最大偏差Δl_max，并将莱斯因子作为一个参量，它允许通过一个简单的数学表达式估计在p和50％接收功率累积分布函数（CDF）之间测量的衰落深度。

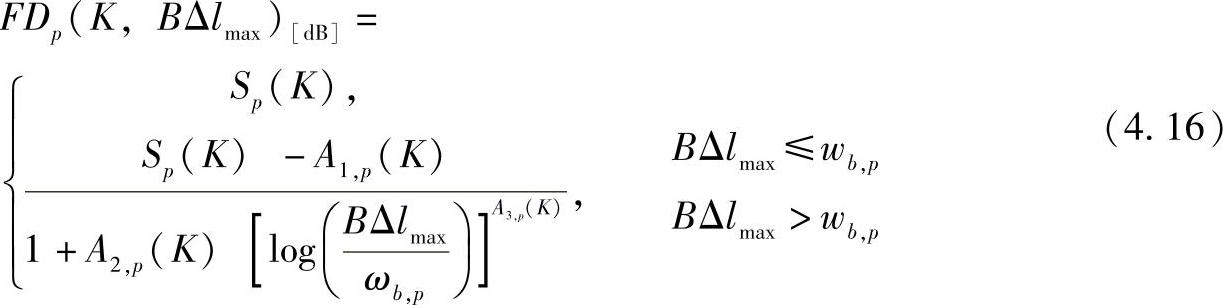
式中，S_p（K）、A₁、p（K）、A₂，p（K）和A₃，p（K）是取决于p的K的函数;w_b，p是取决于p的一个断点值。

对p的任意给定值，函数S_p（K），A₁，p（K），A₂，p（K）和A₃，p（K）可以通过下式估计

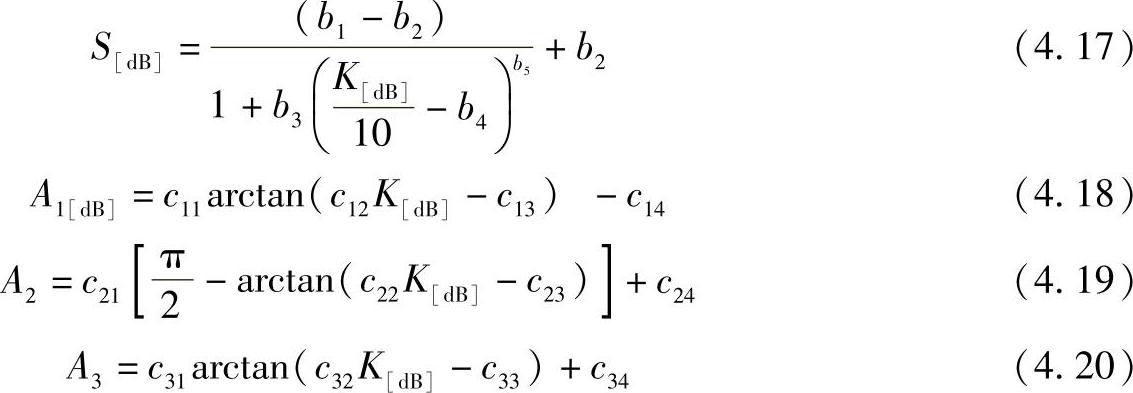
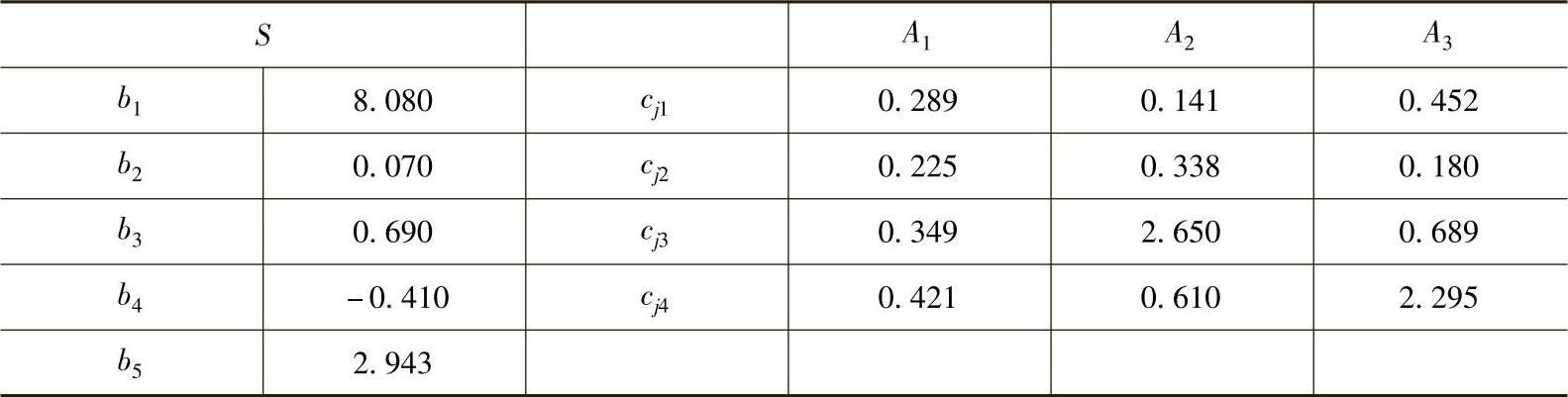
其中，参数b_i（i=1，…，5）和c_jk（j=1，…，3;k=1，…，4）取决于p的值。p=10％时，b_i和c_jk的值在表4.9中给出。在参考文献［CaCo01］和［Card04］中可以找到不同p的b_i和c_jk值。

表4.9 p=10％时，参量b_i和c_jk的值

(www.daowen.com)

因为物理和几何环境特征与传播信道的PDP之间有紧密的联系，可以在不同到达分量之间的传播路径长度的最大偏差和传播信道的RMS延迟伸展之间建立一个简单的关系，因此，连接了先前的2个模型（见参考文献［CaCo03］）

式中，c是光速。

这允许用上述提出的任意方法估计一个给定环境的衰落深度，不管这个环境是由物理和几何性质定义还是由PDP定义。当允许用上述提出的任意方法时，不管是从环境特征开始还是从传播信道的PDP开始，这种简单方法对估计不同环境和不同系统带宽的衰落深度是有效的。

随着第三代系统的出现，数字信号处理硬件的改进，以及对大容量的日益增长的需求，空间域似乎是能增加系统容量的最后关键。这可以通过在基站、MT、或两者上同时利用不同类型的天线来完成;因此，出现了新的天线技术和信号处理技术，包括智能天线、自适应或切换式波束、空间分集合成和MIMO。

为利用这些技术达到期望的链路质量和系统容量，就算法实现方面已经做了很多工作;然而目前尚不明确通过不同系统，在不同的环境下，依靠不同的天线阵列即依赖它们的半功率波束宽度观察到的快衰落深度值。参考文献［CaCo04］中，扩展了参考文献［CaCo01］中的方法，它包含了天线辐射方向图的影响。相对于应用全向天线的情况，这种影响可以通过莱斯因子的变化和不同到达分量之间的传播路径长度的最大可能偏差建模。

作为天线半功率波束宽度的函数的莱斯因子ΔK（α_3dB）的变化，取决于AoAs（或AoDs）的统计分布和考虑的天线类型。假设一个理想的定向天线（假设天线在半功率波束宽度以内具有恒定功率且不为0）和AoAs（或AoDs）的一个具有标准偏差σ_s的截断的高斯分布，ΔK（α_3dB）的值可以估计为

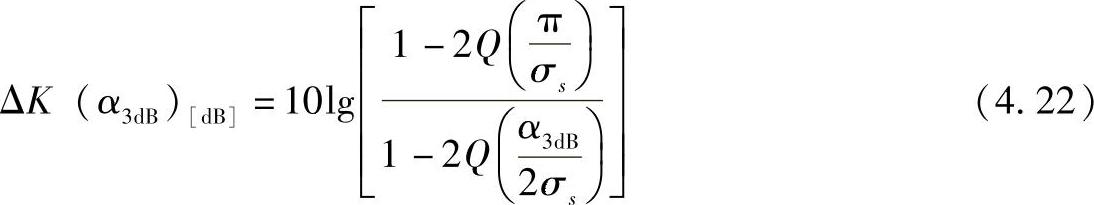
式中，Q（·）是著名的Q函数（见参考文献［Carl86］）。

不同到达分量之间的传播路径长度的最大可能偏差的变化取决于考虑的散射模型，例:通常利用以几何学为基础的随机信道模型（GSCM），椭圆的和圆的是模拟微、微微和宏蜂窝网的最普遍的模型。参考文献［CaCo04］中的结果阐明了这种方法。

关于时变无线电信号测量和建模的参考文献中，通常限制在静态环境中移动发送者或接收者。对实用性的应用，像手机，这显然是很现实的。由于移动散射体的横截面相对固定散射体要小，尽管移动的散射体一直存在，但是它们的影响都被忽略了，至少在室外环境中被忽略了（见参考文献［Cox73］）。

对室内环境，移动物体（人、门、窗等）的散射横截面相对固定散射体而言仍然不能被忽略。而且，对一些应用，例如:无线局域网，在操作时MT通常是固定的，然而一些散射体通常是在环境中移动的（见参考文献［KaFr01］）。

少数对移动散射体的研究可以在与窄带信道的瞬时功率影响有关的文献中找到，例如:参考文献［HMVT94］。对一个更广泛也更普遍的方法而言，宽带测量十分必要。为了达到这个目的，在实验室中完成了宽带测量，其中发射和接收天线之间的距离为6.6m（见参考文献［KaFr01］）。部分视距路径被家具和实验设备所阻碍。在大多数的测量中，由3个人担当了移动散射体。

在1.8GHz，5.2GHz和17.2GHz，带宽为600MHz的情况下进行了系统的测量。由测量值可以看出，在天线移动的情况下，有根本不同的衰落特性和时变脉冲响应形状。这种根本不同导出了一个结论，即不允许（尽管经常这样做）不加鉴别地将从具有线性移动天线的信道的调查中找到的结果和模型，应用到另外一个静态环境中的移动散射体上，如图4.38和图4.39所示。

从全局上看，这些结果已经表明移动散射体的影响不能像经常做的那样被忽略。就移动散射体和/或移动天线对信道特性的频率依赖而言，通过3个不同频带的比较没有发现根本的区别。

作为一个主要的结论，可以表述为，对于一个统计学模型，将一个著名的适用于具有移动发射机或接收机的信道模型，不经任何改变应用到具有移动散射体的信道显然是不现实的。

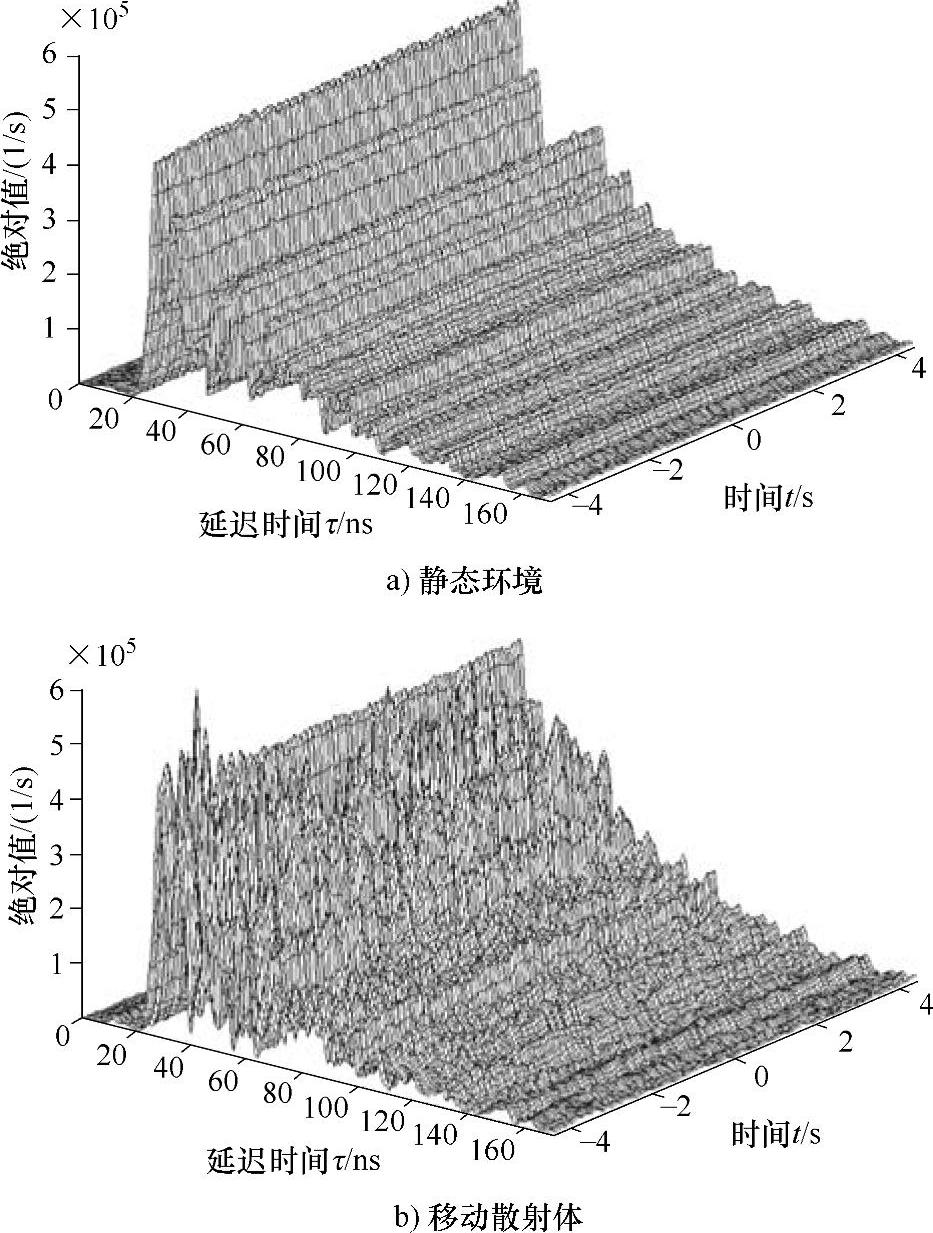
图4.38 在1.8GHz，固定天线下的时变脉冲响应（见参考文献［KaFr01］）