在这一部分所讲的移动信道的性能都被建模为随机过程。在多数的关于信道特性的文献中，已经从对时间序列的运行中推导出了大多数的特性。这种方法，暗含了以下假设（见参考文献［Bult04］）:

1）在考虑之中的随机过程的测量可变性仅仅是时间或者距离的函数，这使它成为一个随机过程。

2）在广义的平稳（Wide-Sense-Stationary，WSS）随机过程中可变性仅是2个取样点之间时间差或距离间隔的函数。因此，平均值应该不取决于时间或距离，自相关函数应该只取决于时间或距离的差异。

3）大部分时间序列随机过程是遍历的，它允许用孤立的样本函数替代总效果。

实际上，这意味着随机过程的平均值应该是恒定不变的，过程中的协方差应该存在，但很难在实际情形中检测。也可以说，在文献中很少有论述证明上述假设是成立的。

一种可能性是保证随机过程既是WSS又是高斯分布，这样的过程是遍历的。然而，高斯性能应该通过中心极限定理推测出，虽然时间序列的分析潜在地假设了其遍历性。Bultitude把无线信道上小于15个多路径组件的事件当作对在信道转移中不能假设具有高斯特性的一种指标（见参考文献［Bult02b］）。因为多径的分布和独立性，比15大得多的时间序列可能需要安全的假设高斯特性。(www.daowen.com)

Bultitude通过对照后来的多普勒光谱对WSS进行测试。他用MUSIC算法从半重叠1m的测量部分提取多普勒参量，计算平均功率加权到达角和分散角的连续方差。任意一个方差的最大值变化超过10％被认为是非平稳的。在渥太华（曼哈顿电网）市中心对1.8GHz的微型蜂窝电话场景的测试，发现了近似的符合负指数分布平稳性区间，“一致性长度”，但是测量显示了更大的间隔可能性。对非视距场景，这些平稳性区间长度的中值介于2.6～3.3m，这取决于场景方向（见参考文献［Bult03］）。Bultitude开发的另一项用于测试WSS的技术是对光谱线中间附近的方差的检查（见参考文献［Bult02b］）。

在决定频率相关函数的过程中，通常的做法是在（平均）功率延迟剖面上利用傅里叶变换，这里假定散射不相关（US）。我们对US的测试是为了直接从频谱中确定频率相关函数，并测试产生的关于任意参考频率的相关函数是否对称（见参考文献［Bult02b］）。Kattenbach已经处理过室内环境中US假设的有效性（见参考文献［Katt97］）。同样由于占主导地位的相关组件的存在，如同在Ricean衰弱过程中，可能使从傅里叶变换得到的结果失真。Salous和Gokalp提出了一个例子，城市中上行和下行链路特性在2GHz处的微小差异将导致频率相关函数的明显不同，尽管功率延迟剖面是相似的（见参考文献［SaGo01］）。图4.31通过直接关联与由傅里叶变换功率延迟剖面推导出的关联相比较，显示了上行和下行链路频率相关函数的不同。

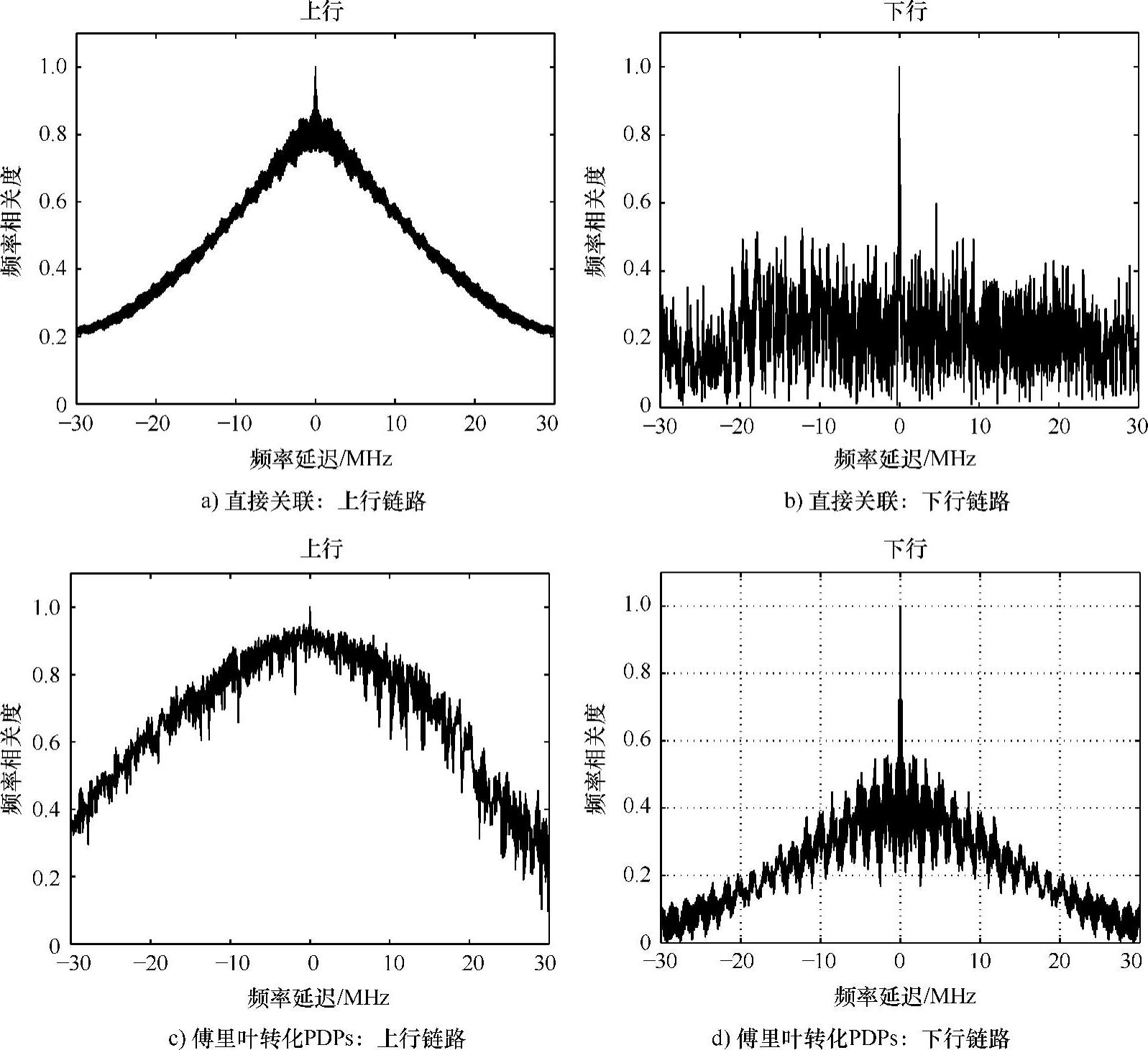
图4.31 在2GHz估计的频率相关之间的对比（在参考模型［SaGo01］之后）