对多维波传输机制的彻底调查是理解信道转移矩阵的空间和瞬间结构的必要条件。通过现场测量得到的信号参量估计值的精确度和可靠性取决于信道探测系统的设计。假设在空间域，天线阵列的设计（见参考文献［TLAP02］，［KaKC02］）是决定DoA估计可靠性的一个参量。由于在实际性方面，如:机械方面、电气方面的构造以及天线阵列的不合格，真实天线阵的性能与所设计和模拟的性能有所不同。因此，校准和评估的方法得到了发展（见参考文献［LaRT04a］，［LaRT04b］）。

天线阵的设计和评估方法是基于利用克拉默-拉奥下界（Cramer-Rao Lower Bound，CRLB）和波束优化的技术。CRLB定义DoA估计的方差限制独立于任何其他参数估计量。它起因于对有关信道参量（例:DoA）观察数据的一阶衍生矩阵的逆协方差矩阵计算。因此，天线阵必须有一个可导的数据模型。为了这个目的，阵列流形的解析函数通常被用于设计和模拟的情况下（见参考文献［KaKC02］）。为简单起见，这些方法通常忽略了天线波束方向图、互耦合以及一些其他的特性的影响或者真实天线阵的不合格。因此，在参考文献［LaRT04a］中提出了一个真实天线阵的基于可导校准测量数据的数据模型。

利用CRLB设计天线阵的方法假设估计算法可以找到最优化问题中价值函数的全局最小值。大多数的估计算法是连续的，这就意味着要逐条路径逐个参量的估计信道参量。这样的解决方案仅能找到价值函数（例:虚拟路径的估计）的局部最小值。参考文献［TLAP02］中同样考虑了波束最优化。CRLB最小化方法和波束优化方法两者应该结合起来，利用在信道测量和分析中设计的天线以得到令人满意的结果。

1.CRLB最小化步骤

在移动无线电信道特征描述设备中，天线阵最优化的一种方法是遗传算法（Genet-ic Algorithm，GA）（见参考文献［KaKC02］）。为最小化DoA估计值的CRLB（最小方差）提议设计一个信道特征系统的阵列。关键问题是选择最佳的阵列几何，也就是找到阵列元素应该安放的位置，以获得能降低DoA估计误差到一个最小值的测量值，可以采取最小方差无偏估计算法，例如ML算法。每一个传感器都被希望有一个各向同性的波束图形。假设对从信号产生的簇集有一定的先前了解，GA能决定传感器的位置，使未知数目和散射体位置的DoAs的平均CRLB最小。

2.波束优化步骤

参考文献［TLAP02］中为避免估计结果是价值函数的局部最小值，提出抑制波束的旁瓣c_k（x，Θ）=x^H_ka（Θ），这里x_k是第k条路径的完整数据，a（Θ）是天线阵关于DoA Θ的正规化导向矢量。在初始化过程中，这个函数通过大多数ML算法计算，例如:EM和SAGE。以一个具有全方位波束成形的均匀圆形阵列为例，最好的旁瓣电平抑制是通过收敛半径r_opt≈Nλ/16＜λ/4sin（π²/N）得到的。深层的抑制可以通过天线元素的波束图形和阵列半径的联合最优化得到。有人发现为得到DoA的最小CRLB，UCA的半径应该尽可能得大。按照波束的旁瓣抑制，半径越小越好。因此，有必要在最小CRLB和波束优化之间寻求一个折中值。

3.实际天线阵的评估

一旦天线阵实现，就可以在消音室测量。天线的响应用所有元素的复杂的极化波束图形描述，这是由垂直和水平极化激励所引起的。记录完整的球形波束图形需要阵列沿一个在阵列相位参考中心的合适的支点的精确自转，并且要求装置有极好的相位稳定性。测量的波束图形在方位角和振幅上是离散的。由于波束图形以2π为周期，可以用离散傅里叶变换将波束图形转化为有效的孔径分布函数（Effective Aperture DistributionFunction，EADF）域（见参考文献［LaRT04a］，［LaRT04b］）。EADF矩阵用离散波束图形的方位角和振幅的傅里叶矩阵通过二维傅里叶变换计算得到。因为它是以图4.29（右）中的有限支持区为特征，EADF在概念上允许一个相当大的数据压缩。另一方面，它允许对角度参量的导数进行简单分析计算。(www.daowen.com)

一旦存在DoA费歇尔信息矩阵（Fisher Information Matrix，FIM）的一阶倒数，就可以计算它的任意测试场景的逆CRLB。FIM结构的调查研究和开发对设计一个强健并有效的参量估计器是必不可少的。最简单的场景是一个单独的碰撞路径场景，这将在下一个例子中进行分析。它与拥有192个元素的SPUCPA有关。在这种场景下，FIM是对角线矩阵。在图4.30中，方位角的CRLB与试验中得到的方差相比较。对于在SPUCPA覆盖扇形中任意方位角/振幅对φ，θ，方位角通过ML过程（见参考文献［Rich05］，［ThLR04］）进行估计。这个实验重复进行了64次。CRLB的噪声电平被调整以与保持不变的观察的设备噪声相匹配，设备噪声是取决于17～18dB主瓣方向（θ=90°）的SNR。这种评估方法在更加复杂的场景中同样有效。

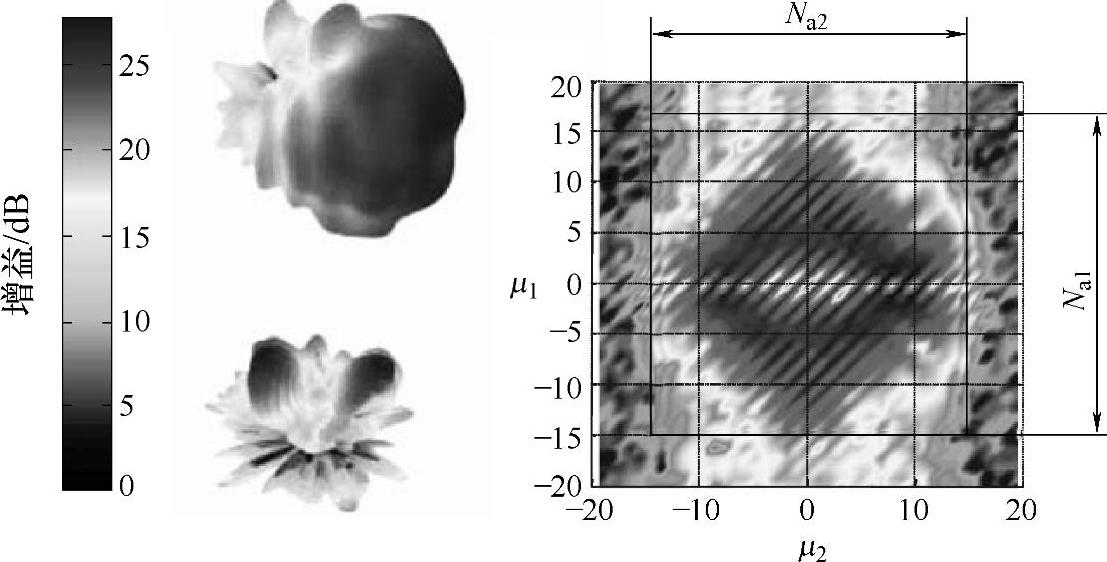
图4.29 垂直和水平激发（左）的极化波束图形以及相应的SPUCPA的垂直激发的EADF（右）

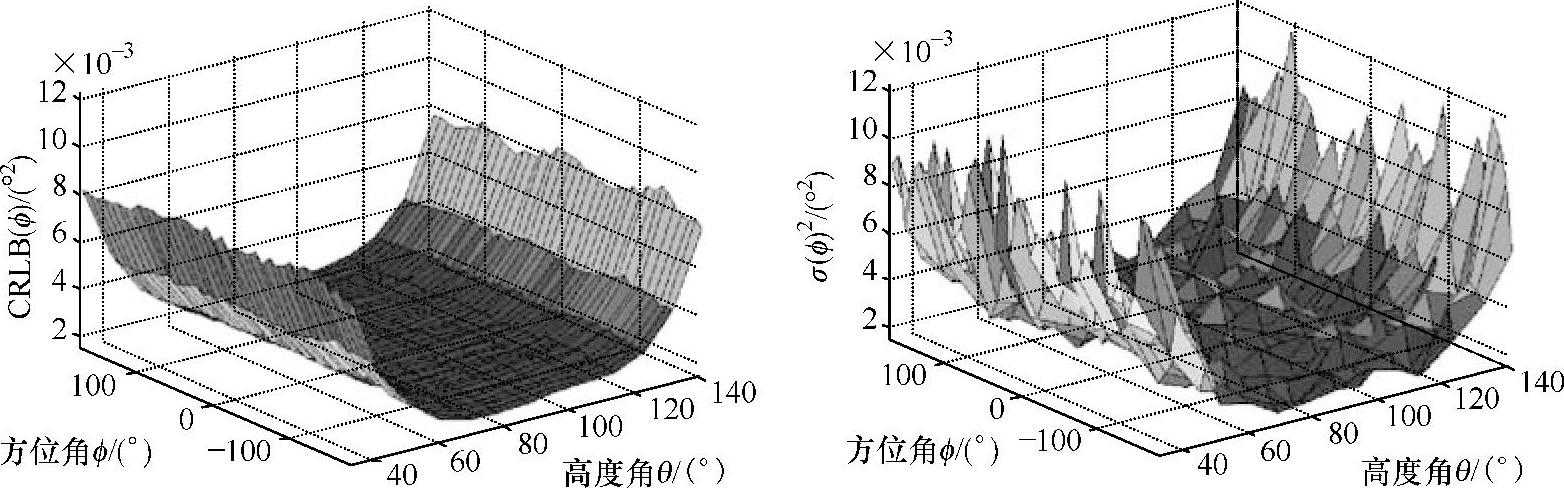
图4.30 到达方向方位角的估计值的CRLB（上）和估计方差（下）对比真实的方位角和高度角范围

深一层的，上述描述的方法可以像在参考文献［TLRT05b］，［ThLR04］，［Rich05］中阐明的一样用于ML参量估计。在这里，它被用于定义估计DoA/DoD参量的可行方差的基本限制，并依照CRLB检查估计过程中得到的参量的可靠性。

参考文献［MuSV05］提出了另外一种估计多维信道探测性能的方法。其思路是利用已经存在的参数测量数据创建一个与原始信道信息非常相似的资料组。这种方法基于测量阵列在校准测量中得到的辐射方向图与参数化传播数据的联合。通过这种方法，可以创建一种对多径信号众所周知却又现实的测试数据用来研究，例如:估计的角分布的正确性。