积分法是描述电磁波的最准确的方法。然而，由于这些方法需要大量的计算机资源（包括内存和处理时间），在电信工程中，此方法还不能被应用在波长较大的情况。COST标准试图缩小这一差距。

1.全矩量法

当然，这些方法已被应用到结构计算中，这些应用是在限制如（元素智能）天线大小（见参考文献［VeLC02b］，［TrSi02］，［TrSi03］和［NdHH04］）的情况下使用。在这里，我们把重点放在更加具体的天线优化设计上，并以此作为主要目标，用数值方法表示这些天线所接收的不同波的优化，详见4.4节。文献［VeLC02b］描述了具体的三维阵列天线设计，它要求允许以一个明确的方式接收信号和这些信号之间的不同方向，这个在平面阵列中是不可能的。由12个补偿电容组成的这种球形阵列是在分段正弦伽辽金法的基础上设计的，它利用的是数值电磁编码（Numerical ElectromagneticsCode，NEC2）。因此，该五边形区域已经逼近2个同心五边形和径向延伸线。我们的研究重点是把对两个网络参数和辐射模式的供应线路以及之间的耦合元素的影响降到最低。图4.1中显示的是具体实现的十二面体天线，它有低于-23dB的耦合值，而模拟预测是-22dB。然而，这种匹配现在是不能完全预测的（在4900～5100MHz频段是-18dB，而该计划预测的反射损失是低于-23dB的）。

图4.1 具体实现的十二面体天线示意图

参考文献［TrSi02］和［TrSi03］使用的是另外一种矩量求解（WIPL）方法，这种方法用两个、三个或四个元素计算5GHz附近（4.74GHz）的单极设计的平面圆阵的耦合阻抗。这里的主要目的是计算MIMO信道的平均信道容量。该耦合的影响将在5.3节中讨论。文献［NdHH04］提出了一个新的MoM，伽辽金法解决方案比较了40个具有经典正弦分布的半波长偶极分段线性（三角形的结果）基础函数的结果。和前两个文献一样，其最终的目标是确定一个2×2的MIMO系统的容量。

矩量法，不仅被用于有限空间范围（尺寸为几个波长）的天线，而且适用于计算天线尺寸远超波长范围（事实上，一些达到1000倍波长）的情况对传播的影响。COST标准为了修正二维方法以让三维与二维有几乎同样的计算量，甚至低于二维的目标进行了很多工作。本文为了达到减少计算量的同时充分利用目前的计算方法（如［KeCu03］所述）目标使用的是维纳-霍普夫技术来寻找混合场积分方程（Combined Field IntegralEquation，CFIE）。这些都是分析菲涅尔积分比较容易的组合。全积分方程方法和被截断平面的分析公式相比仅有临界入射不同。举一个实际的例子，在970MHz下分析一个德国地形剖面情况，我们可以看到这两种方法计算结果几乎没有差别，即使钢板长度约30λ。另一篇文献［BrCu01］引入积分微分方程，其中包括表面横向梯度的传播方向。通过用一个二阶多项式近似表面横向部分的相位，在良导体（Perfect Electric Conduc-ting，PEC）内二维磁场积分方程（Magnetic Field Integral Equation，MFIE）可以改写成一维积分方程。其中积分方程涉及计算菲涅尔积分。该方法不仅被应用于像在100MHz和1GHz的平滑倾斜楔这种理想情况（对共极化和交叉极化），还适用于实际地形如丹麦和爱尔兰更复杂的数据。我们得出结论，共极组件确实有不错的适应性，但现在交叉极化是十分重要的，因为多样性的偏振效应需要精确建模。解释如图4.2所示。

2.物理光学模型

参考文献［DMSW03］比较了标准基尔霍夫定律和一种名为标准随机散射的新方法。在这里，把整个表面按照不同的方向细分为小的平滑的部分。假设一个随机正态分布和高斯自相关系数，梯度绝对值服从均值为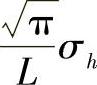的瑞利分布，其中L是相关距离，σ_h是粗糙度方均根。虽然基尔霍夫定律会导致从平面尺寸上散射模式比相关散射模式更具有独立性（在这里考虑一个8×8λ²平面），但是随机散射方法也确实证明大多散射是由粗糙度引起的，这个结果可能会比传统假设基尔霍夫固定相位情况下大得多。对于这种情况，假设相关距离为4λ，粗糙度为0.35λ，我们在离平面2000λ处计算所有参数值，和基尔霍夫情况对比:得到一个完整的衍射图案，最主要的散射区域有明显地减小。

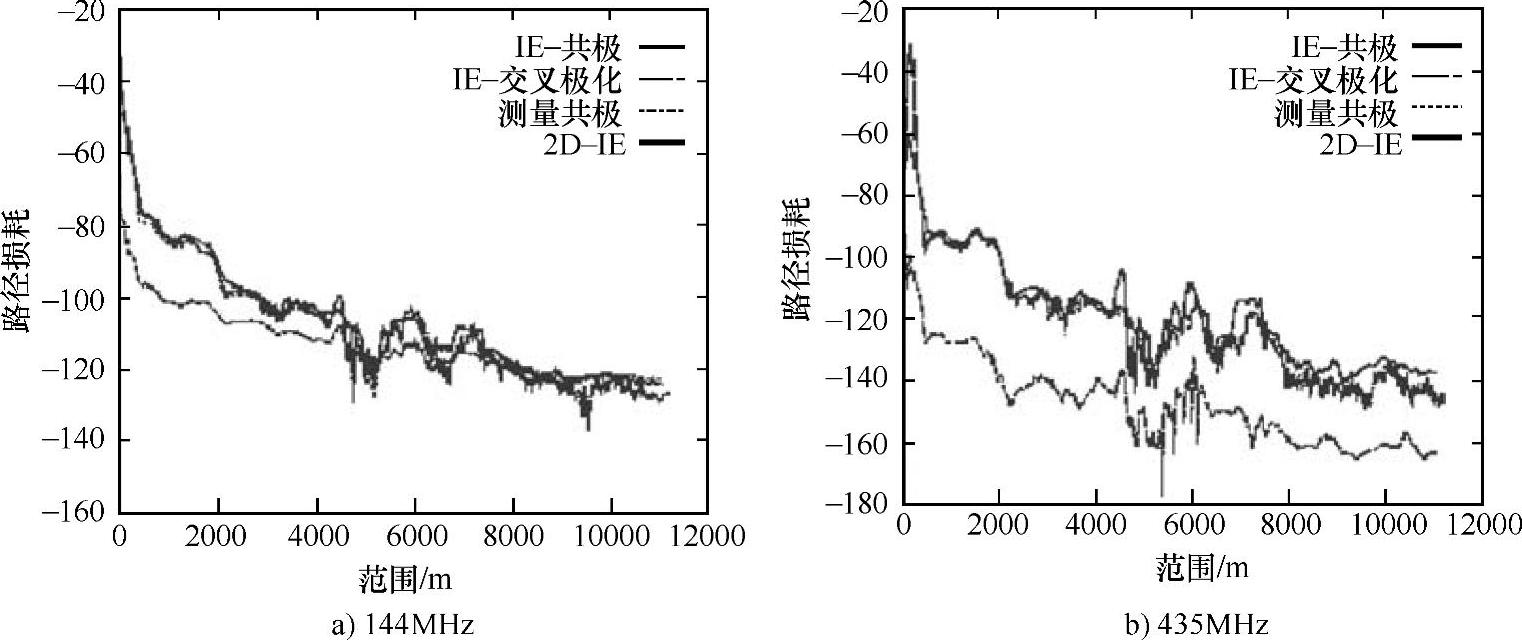
图4.2 丹麦的共极和交叉极化地形区域

这就涉及一个对于大型对象或关闭发射机/接收机物理光学（Physical Optics，PO）的问题:平面波近似失效，如果散射体的体积增加，就会导致该散射区域继续增大。因此，必须找到其他的解决方案。参考文献［LCDC02］正是基于这个目的，使用了抛物相位近似，这种近似法在以前的COST标准中被命名为COST标准259—灵活的无线个人通信（COST-259）。本文探讨了这种菲涅尔法的很多改进方式，如(www.daowen.com)

1）在近场使用的公式;

2）在有限厚度和材质特性（介电常数和磁导率）限制下的反射板中利用内部反射;

3）集成中心最佳选择，这是有效应用这一方法的关键。

对于最后这种情况，我们用了7种不同的方法（首先是平凡解）进行了研究。结果表明，使用最好的拟合方法（最佳意味着抛物相位尽可能与真实球体的相位相接近，即达到及涵盖二次计算）来求解平凡解，每秒的浮点运算数目（FLoating Pointoperations per Second，FLOPS）也只能得到4次不错的结果，消声室平板的模拟和测量也吻合得非常好，无论是在振幅还是相位上，振幅图如图4.3所示，相位图如图4.4所示。

3.模态扩展模型

由于这种方法专门适用于封闭空间，在［Kyri03］中已应用本方法作为在因子为K的走廊评价方法。事实上，射线跟踪方法不太适合这类问题，因为在这种结构的边缘反射可能会变得非常大。考虑相同的反射系数的损失（包括介质和传导），我们评价了一些不同的传播模式的优劣。连续分量估计被证明是最稳定的算法，它优于统计方法或ESPRIT算法。这也证实了我们直观的预期，即K因子会随着损失增加和尺寸减小而增加。

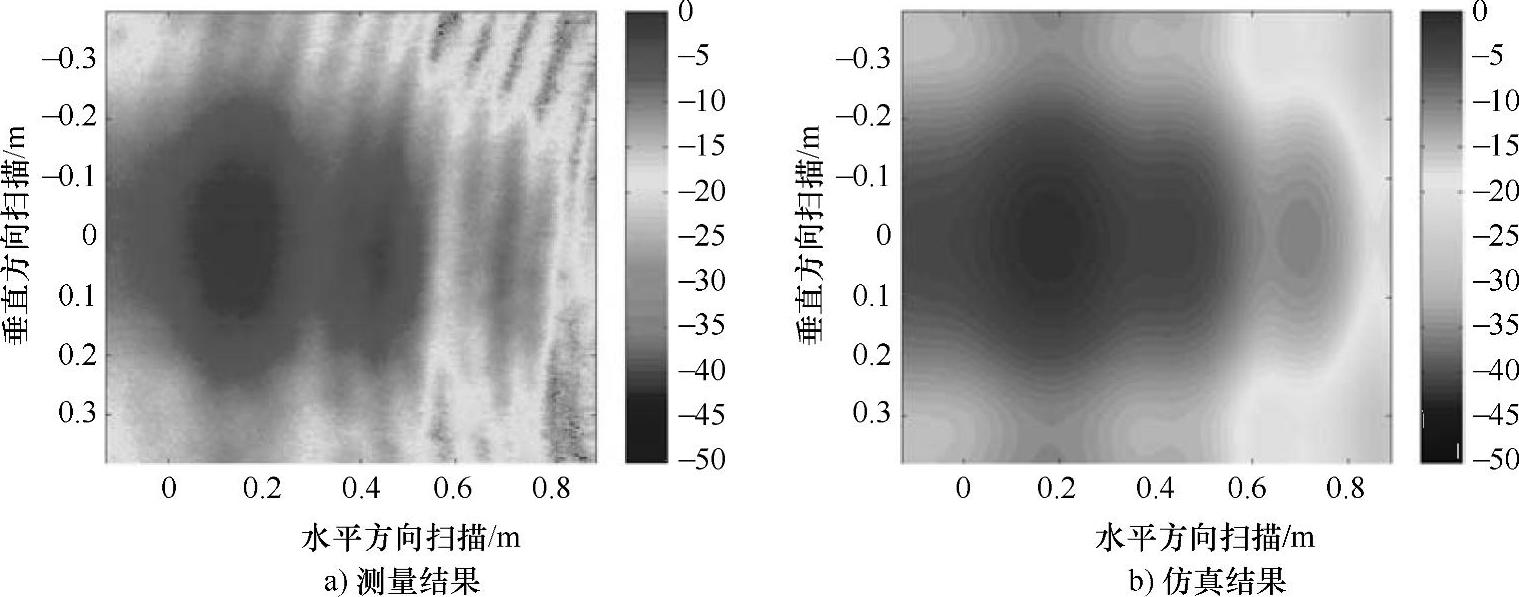
图4.3 5.8GHz下0.35m×0.5m×0.02m有机玻璃板反射区域振幅图

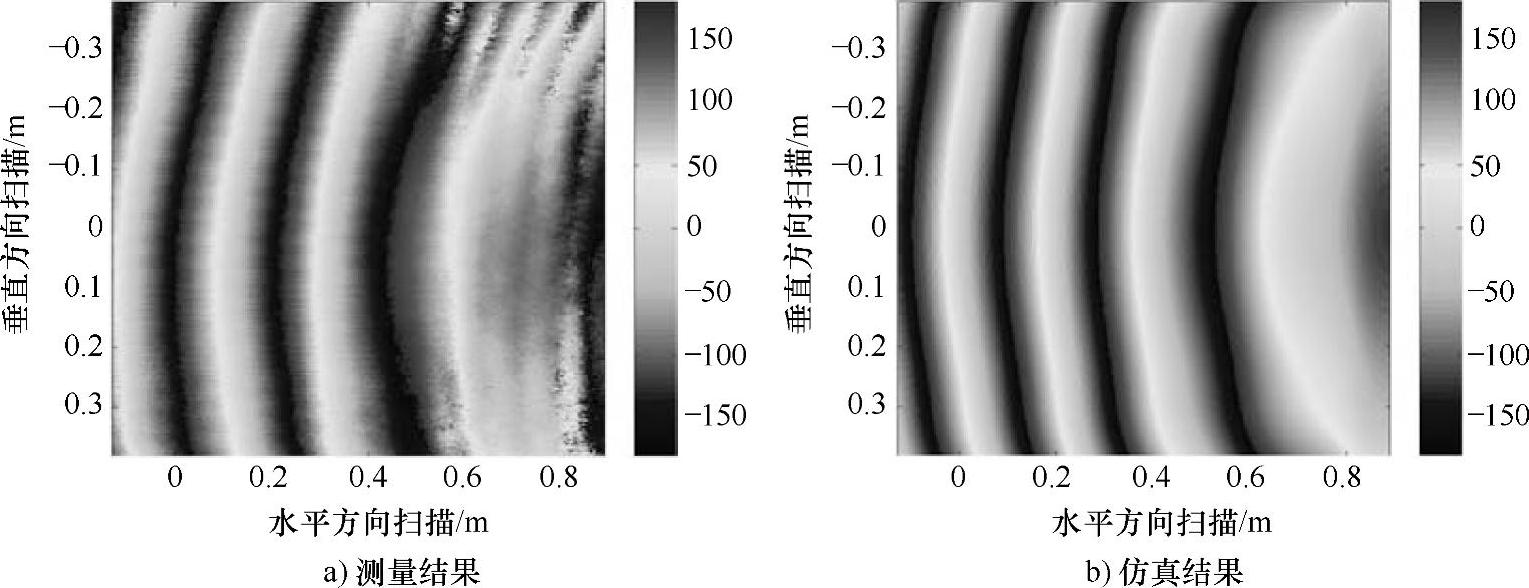
图4.4 5.8GHz下0.35m×0.5m×0.02m有机玻璃板反射区域相位图