同步采集过程的分析方法和具有最佳非周期自相关特性的结构序列的方法（以最小的总模拟概率交替）已经是在数字传输初期的多次分析的主题。只有少数研究探讨帧长度与同步序列的长度和结构之间的关系。但是，与其他类型的错误相比，由于不完善帧同步造成的性能下降比较小，该领域几乎被忽视，除了参考文献［BaSD02］，［BaSt03］。然而，新的解决方案和高数据传输速率提供了更多自由层次。几乎所有参数的设计是必需的，所以必须开发更合适的分析工具。

序列分析的背后存在一个数学家和工程师都感兴趣的过程——对一个由随机等概率L-进制数据构成的定长序列的搜索。历史性的工程方法开始了双缀的介绍，这是梅西.J教授提出的一个名称。它是指一个长度为n≤N的子序列，既是观察的长度为N的一个前缀也是一个后缀。序列是可由双缀指标h（n），n=0，…，N完全表示。如果一个双缀长度n存在，或者如果n=0，h（n）等于1;否则，等于0。

目前的技术执行一个序列搜索是在指定的距离内。在符号级上，这相当于对一个设定的序列搜索。对于这样的搜索，新特征被引入:交叉双缀。交叉双缀是一个长度为n≤N的序列，它是第i个序列后缀，也是第j个序列的前缀，都从M序列的观察组中选定（i，j=1，…，M）。相应的交叉双缀指标h_i（jⁿ）等于1，如果一个交叉缀长度n的存在，例如二进制序列p_i=0001和p_j=0011有3位交叉双缀h_i（j³），明显地h_i（j³）=0。如果i=j时h_i（jⁿ）是指一个经典双缀指标h（n）。默认值对于交叉双缀指标是

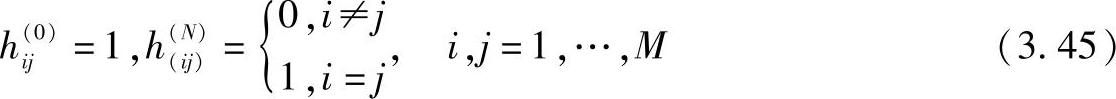
搜索刚好在第k步完成的概率（一个搜索过程中的一个离散的概率密度函数-PDF）等于

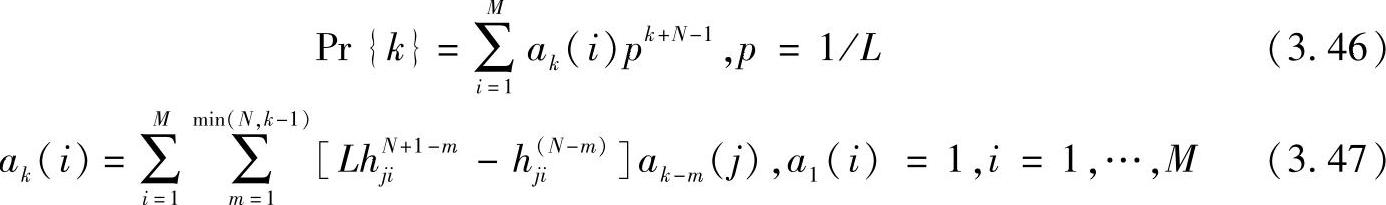
其他（预计持续时间搜索，方差）统计参数可以从这个中得出（见参考文献［BaSL03］，［BaSt04］）。这个结果（见参考文献［Baji04］）的修正产生了在一个帧中持续时间的搜索的PDF，其中一个同步序列是定期插入到通常杂乱的流中，因此，是随机等概率数据，如图3.28所示。

图3.28 在一个帧内的搜索(www.daowen.com)

出现的结果之一是存活概率P_SV，即不出意外的同步序列模拟的概率，考虑到搜索开始于在正确的同步的位置偏移S（最坏的情况下为S=1）。图3.29显示了P_SV对帧长度F和序列长度N的依赖性，如果允许的汉明距离为H=1（此情况下，在设置中序列数目M=N+1）。应该被指出的是“全0”序列，以及无双缀的序列00…01，有P_SV=0;图3.29给出了各种允许的汉明距离的影响。

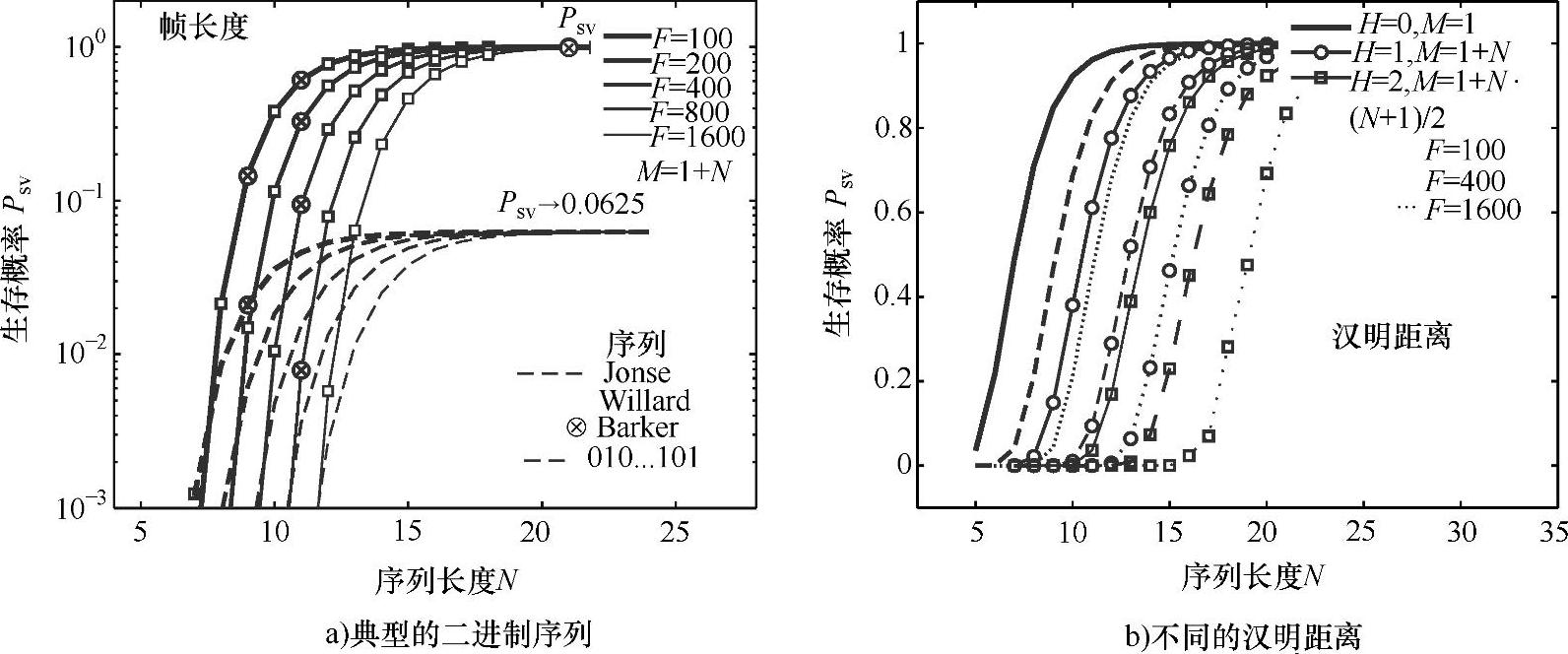
图3.29 生存概率

如果序列长度N增加时，生存概率达到极限值。对于好的序列，这个值等于1，即序列是模拟前的正确位置是不太可能的。然而，在P_SV=1的序列中，其他的区别可被观察到，如图3.30显示了Pr｛k｝（PDF）的例子。如果H=0，所有的无双缀序列具有相同的PDF，当H=1时，好的序列是（例如琼斯的00011011和威拉德的00100111）相似的。如果H=2，威拉德的和琼斯的序列有相同的生存概率，虽然它们的PDF略有不同。如果适当地平均（见参考文献［BaNa04］），派生的PDF对帧采集时间的预期值能够表示著名Häberle的曲线，冗余α=N/F作为参数。当在序列距离H=1的序列被允许，曲线显示了这个情况。如果只有一个（M=1）序列被认为是正确的，虚线代表采集时间。对于更短的帧，后一种情况下产生更好的结果（更短的采集时间），但它不是一个最佳的解决方案。当序列长度增加时，达到近似饱和度部分的P_SV曲线是图3.29，M=1时采集时间饱和，而多搜索（M＞1）的采集时间提高了。

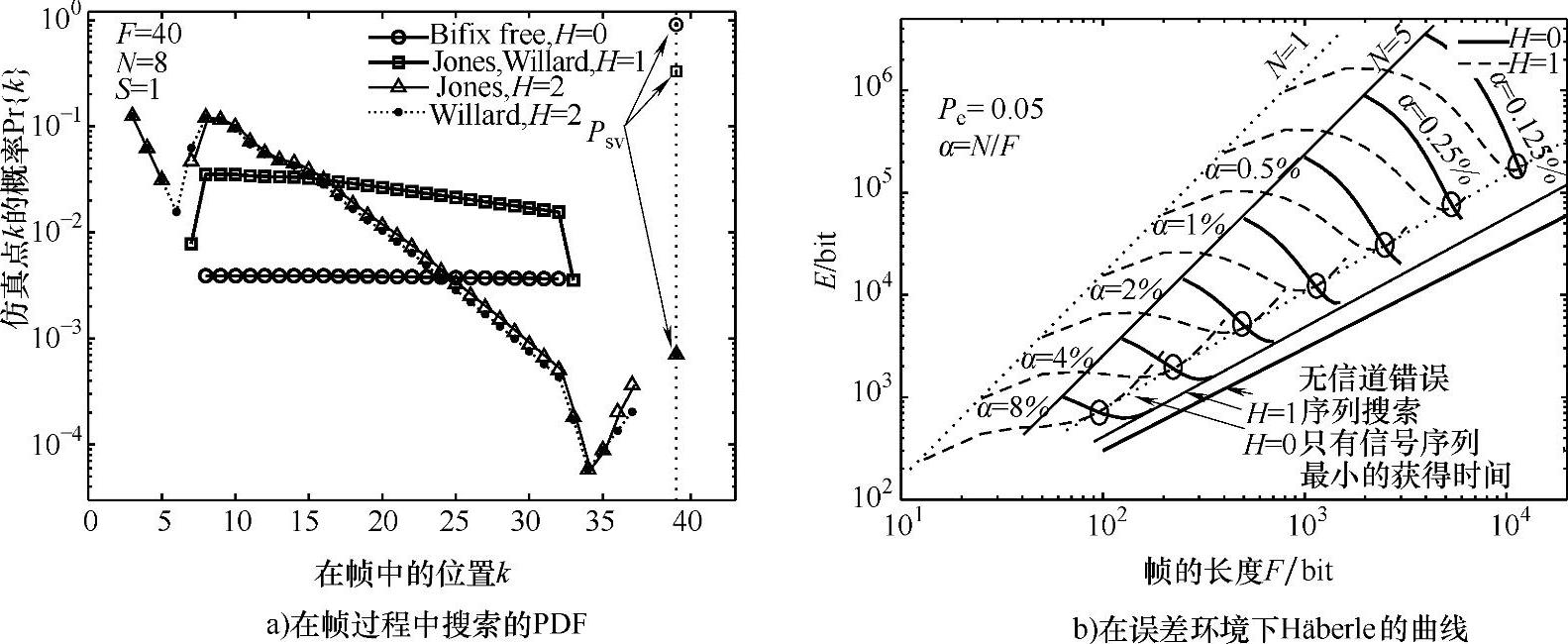
图3.30 在帧处理过程中搜索的PDF和在误差环境下Häberle的曲线

这项工作可能会扩大到多层次（L＞2）的情况。进一步，目前的结果表明，双缀和交叉双缀指标实际上是概率，而整个分析可以转移到非等概率情况。最后，计算的分析工具是在生物医学领域时间序列分析中实施的。