1.迭代接收机中APP辅助载波恢复

在编码系统中尤其是在Turbo编码系统中，我们考虑同步（即载波相位和符号定时恢复）和解码问题。我们引入一个新的概念“APP辅助估计”，其中从MAP解调器（用在Turbo解码中）中获得的对数-似然比被用来在迭代同步/解码器中辅助评估。我们参考了在Turbo编码BPSK系统中的载波恢复来详细描述了这个，并且对常规的同步和解码分开的系统，证明了其重要的性能优势。我们也给出了Turbo编码的QPSK和在Turbo编码BPSK中的定时恢复的一些大体结果。

我们假设在AWGN信道中接收信号r_i=A_iexp（jϕ_i），A_i是系数，ϕ_i是相位，根据由于载波相位误差和AWGN而变化。第i个接收信号的对数-似然函数是

其中，²定义为噪声功率，L_e（i）=In[p_i（1）/p，（0）]是由Turbo解码器获得第i个数据比特最大对数-似然比，块似然函数是。

为了找到最大似然函数值，采用下面的简化形式。我们可以方便地通过傅里叶序列来近似这个函数。

由于仅含余弦项

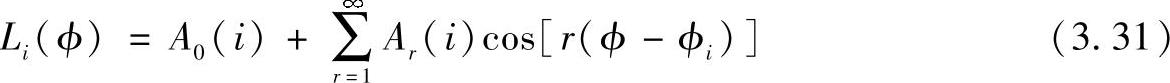
实际上，我们可以知道可以忽略二阶以上的项幅度，则

L_i（ϕ）≈A₀（i）+A₁（i）cos（ϕ-ϕ_i）+A₂（i）cos［2（ϕ-ϕ_i）］（3.32）

这个近似允许通过ϕ直接计算最大似然函数。一个类似的方法可以应用到符号定时恢复上。详情参考参考文献［ZhBu01］。

2.时间和频率高度选择性信道中OFDM的Turbo信道估计

由迭代解码器的软信息辅助的迭代CSE技术的一般原则可以被应用于具有深度的时间和频率选择性信道的OFDM系统中。但是，OFDM情况使用恰当的时间-频率定位符号下可以带来特殊的额外的特征，而这个符号可以被用作CSE额外的先验信息。深度时间和频率选择性信道需要适当的二维离散的信道的时间-频率转换函数。OFDM传输能够简单的实现这个。CSE估计器本身是基于迭代EMA的ML估计器实现的。进一步的细节，详见2.2节，也可以参考参考文献［Jaff01］，［Jaff02］。

3.同步器和检测器联合的迭代EMA的阐述

我们可以知道迭代EMA是如何提供对信道参数（相位、延迟、幅度）的最大似然估计。EMA迭代和Turbo接收机的迭代融合结构被提出。更特别地是考虑了相位辅助定时恢复和联合定时相位恢复并对其进行了比较。介绍了在每种情况下，同步器性能的仿真描述:估计器的均值和均方误差和同步的系统的误码率。

参考文献［DeLR77］表明，在EMA方法中，数据是一个难以获得的观察值。把EMA理论应用到相位ϕ和符号时间τ的联合估计上，我们可以得到迭代机的第n次迭代，形式如下:

式中，r是在信号空间响应中接收到的信号;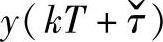是匹配滤波器在采样点kT+ˇτ的输出;K是观察的长度。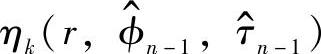从Turbo解码器的软信息的使用中获得。

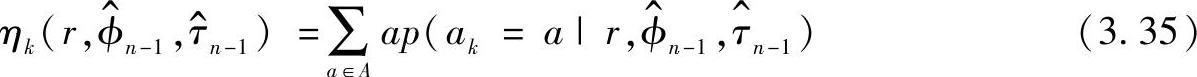
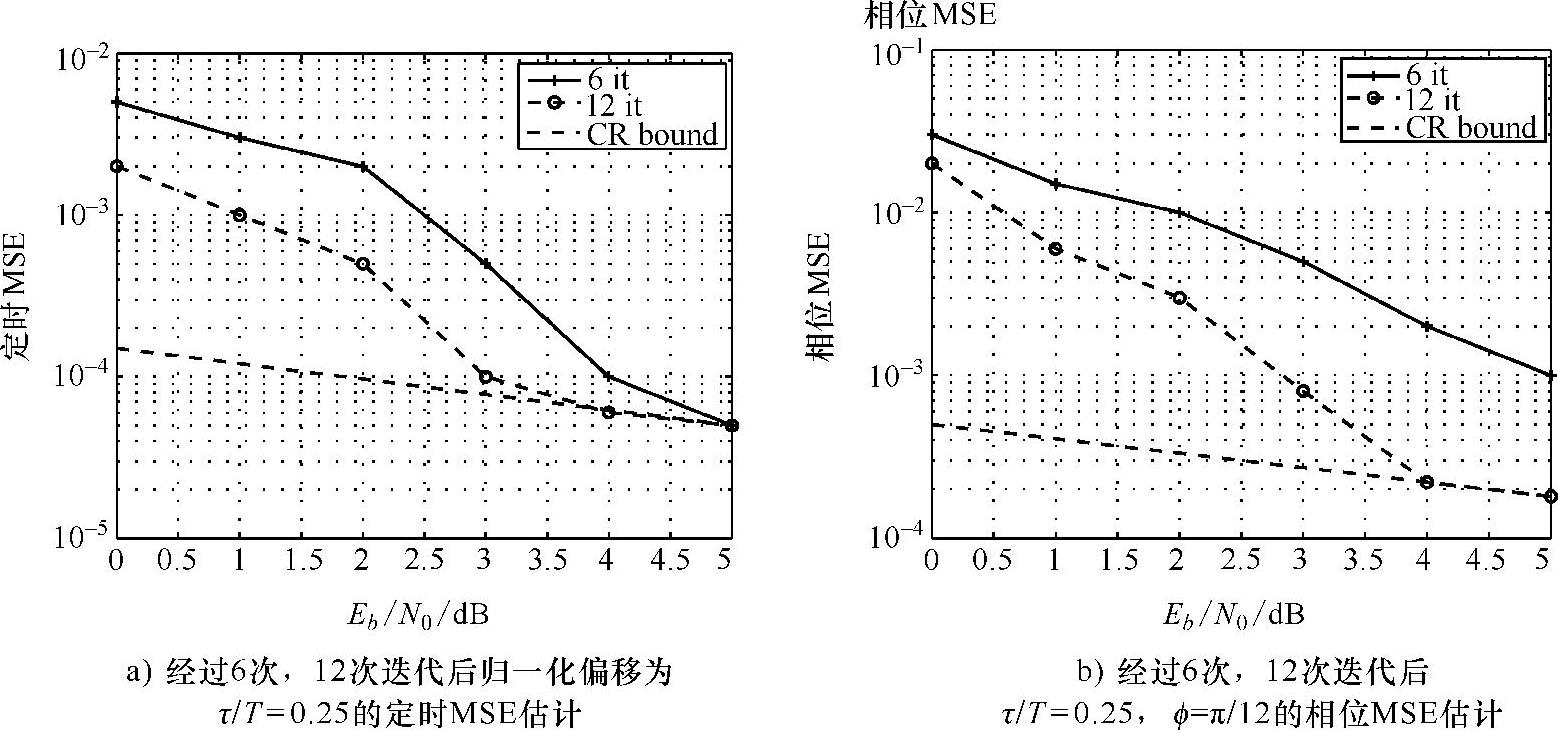
图3.20 定时的和相位的MSE估计

A是符号字母表。图3.20中，仿真的结果显示了联合时间相位估计器的性能。细节处理参见参考文献［NHDL03］。

4.迭代软判决定向（SSD）线性定时估计器

我们可以把非常规形式的迭代定时估计器的问题转化为EMA方法。我们提出了线性定时估计，它可以从每次迭代估算时间估计的Turbo系统传输的软信息中获得利益。基于目前描述的EMA方法，把估计器和同步器拿来比较。同步器的性能由仿真结果给出，并且比同时考虑收敛速度和范围的EMA的性能要好。

在EMA符号定时方法中，最大化步骤是用急剧下降的方法来实现的。这可以减少对可用观察子集的线性操作。自然下一步是通过一个高效和公平的线性估计计算下一个估计的更新。估计器在第n步的更新纠错是:

式中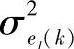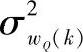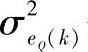，，，，分别是白噪声和背景噪声的同相和正交分量的方差;y·是匹配滤波器输出的时间导数;η_k，n是在迭代检测中使用软信息得到的信息符号的后验平均值x（t）是所提出的余弦滤波器，并且(www.daowen.com)

图3.21 线性迭代估计器在E_b/N₀=4dB时的均值

图3.21中，性能结果显示利用急剧下降最大化的EMA估计器和最新被提出的线性的均衡器经过大量的迭代之后具有相同的均值。线性的均衡器比EMA的估计器更快地收敛到一个确切的时间偏移。就如所期望的一样，当计时误差增加时，两个估计器有不同程度增加，这是因为线性的估计器充分利用其“延长”的观察设置（即无论是在同相分量还是正交分量）。我们观察同样的行为来得到均方误差。但是，请注意这次最终的性能不再相同。确实地说，当EMA估计器达到Cramer-Rao界限时，线性估计器的曲线比其略高停留在其上面一点点。

5.融合SP和EMA算法的消息传递同步技术

我们在因素图和和积（Sum Product，SP）算法框架中考虑Turbo同步。与同步参数相关的SP算法信息近似为狄拉克函数。这种近似需要在每次迭代时解决ML问题，作为一个先验的知识，所考虑的似然函数通过考虑符号外赋信息建立。我们通过EMA算法解决ML问题。然后，显示了在Turbo编码传输特定情况下，基于EMA的Turbo同步框架（在前面的小节中提到）实际上是这里提出的方法的近似。对于Turbo编码和比特交织编码调制传输，在载波相位估计的特殊情况下该方法是通过模拟来描述的。参考文献［HeVa05］中同步方法的结果表明虽然执行起来很简单，但是非常有用。

6.Turbo均衡中对块衰落信道的软估计的子空间方法

Turbo均衡的性能很强地依赖于CSI的质量。在块传输系统中，基于包含在每个块中追踪的符号的逐块的信道估计通常是可以进行的。更高的估计精度可以从扩展追踪中获得，而这个扩展追踪是通过合并多个块（Multiple Block，MB）和每个区块内使用追踪符号和软值的数据符号得到的。对于块衰落信道，基于这种方法的软迭代MB技术在参考文献［MoNS04］中得到，其中衰落在一个块内是恒定的。由于终端的移动性，每个块的衰落是不同的。

由于Turbo处理通常在L＞1的数据块集（L由交织大小而定）中进行，MB的方法利用了这个延迟，来改善慢变化的信道参数估计的准确性。MB的方法取决于这样一种假设，在多径信道中联合块的延迟仍保持不变，而不同块的衰落幅度各不相同。因此，不同路径的信道响应跨越的子空间（时间子空间）是常数，可以（L大时具有高精度）由L块接收的信号的平均来估计，而快速变化的参数必须逐块更新。当用于Turbo接收机时，MB的估计可以进行修改，来整合由信道解码器反馈的软信息。由导频符号获得的初步估计通过扩大具有软值的信息符号的追踪，在随后的迭代中重新定义。

图3.22 对于具有基于追踪和软迭代SB-MB信道估计的Turbo均衡中的BER性能与E_b/N₀的关系曲线

相对于传统的基于训练的单块（Single Block，SB）方法，图3.22给出了具有软信道估计的单用户单天线Turbo接收机，MMSE的单输入单输出（SISO）均衡和对数似然-MAP的SISO解码体现的软MB估计的好处。软MB方法被证明是超越所有的基于训练的和SB方法，并且密切接近已知信道的性能。

7.SDD和EMA CSE的迭代译码网络

在这里，在一般迭代译码网络中我们为联合检测和CSE的迭代建立一个总体框架。前面描述的CSE的两个特殊情况（SDD和EMA）是广义的，并且被放入一个共同的总体框架。两者都具有从解码网络中反复改进的能力，但都表现出不同的特性和对迭代方案有不同的可能性。在具有相位旋转的AWGN信道中对串行级联码的QPSK映射的一个简单的应用进行了研究，以证明均方误差（MSE）模糊解析和收敛行为方面的算法之间的差异。

SSD方法是基于数据排除原理的迭代完成，通常在信道符号q层直接执行。使用反馈措施的估计的预期因素形式必须取决于近似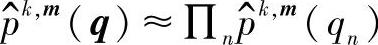。迭代的复数k，m分别描述了在CSE和解码循环过程中（向前向后算法）的迭代，信道参数的最后迭代器是

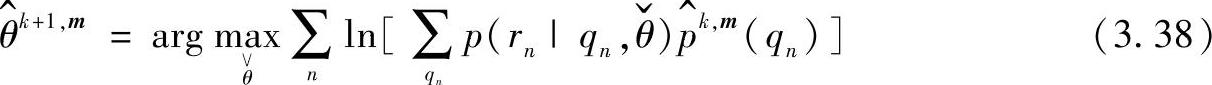
右边取决于迭代量度k，即在CSE中迭代只通过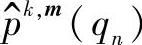，它对给定的m来说是固定;因此，它只对在k和m索引循环这一步时有意义。

在数据传输中EMA算法在CSE问题中的一个应用通常是通过设定等于数据y=d的不可用观察来完成。边缘化的操作p（q_n｜r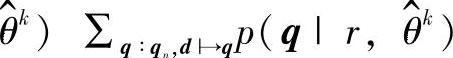，正是SIS模块提供的，并且由于一个情况q∶q_n，d｜→q能够正确地代表了没有近似的编码结构。最后的CSE迭代是

把这个结果和SDD情况比较。不像SDD，即使对固定的m，右侧也取决于k，并且迭代循环可以独立运行。对k次迭代和改善估计的可能性可以节省昂贵的解码计算迭代必要的次数（向前-向后算法）。具有迭代SDD/EMA CSE的一个网络的例子如图3.23所示。

图3.23 迭代非参数SDD和EMA解码网络——多维反馈系统（串行级联网络的一个例子）

模拟结果如图3.24所示。其中最引人注目的是EMA CSE对初始估计的强依赖性（不像SDD情况下），如果不解决歧义的先验，将导致同步失败的概率很高。另一方面，EMA CSE收敛比SDD的情况下更平稳。SDD和EMA之间的一个重要区别在于不同的可能的迭代方案;在EMA的情况下，解码网络中给定的固定的迭代次数的CSE提高了估计的质量（见参考文献［SyBu04］）。

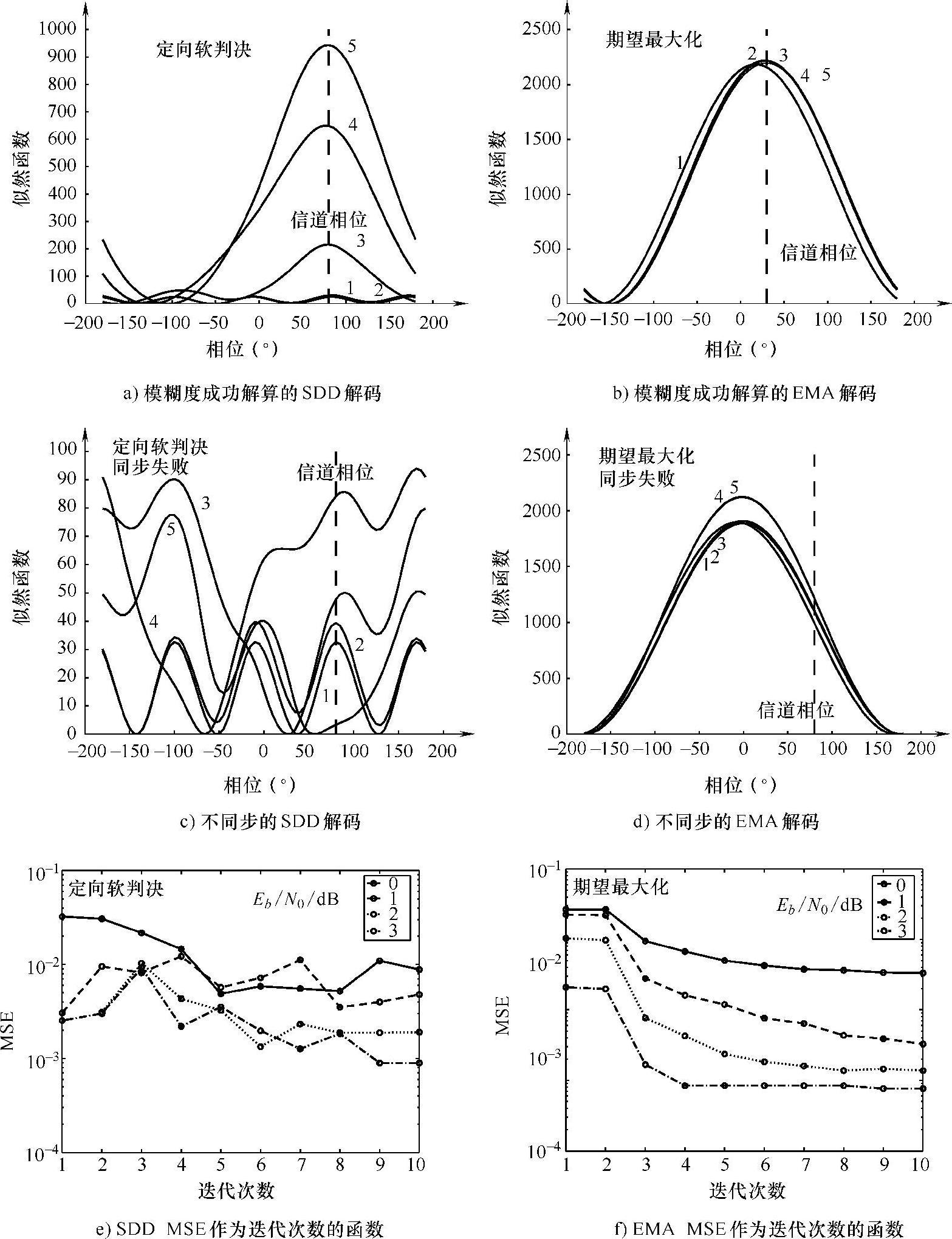
图3.24 模糊度成功解算和不同步的SDD和EMA相位估计的多种结果（真正的信道相位如虚线所示。解码循环迭代次数是一个参数，γ_B=2dB）