在应用于数字用户线（Digital Subscriber Line，DSL）、广播（DAB，DVB-T）和WLAN（HIPERLAN/2，IEEE802.11a）之后，OFDM技术将用于速率更高、带宽更宽的移动系统。因此，当前的任务是提高OFDM技术的性能以及改善缺陷和传播环境。

在过去的10年里，人们已经在这方面做了很多研究。随着日益增长的对高速率与移动性的需求，研究人员表现出来的对于在时域和频域内的高选择性信道的兴趣也越发的浓厚。此外，要想增大OFDM系统的容量，在MIMO系统中用于信道估计的天线阵列的应用也变得更加重要。

因为信道估计器的效率和性能与信道模型的精确度与准确度紧密相关，所以信道模型的选择与定义至关重要。

1.Turbo信道估计

在参考文献［JaSi00］中提出了一种基于信道相关矩阵的Karhumen-Loeve（KL）分解的信道模型。此信道模型考虑了OFDM信号的时频块（见图2.8），在时域和频域描述了信道。由时隙-频隙相关函数可得到理论上的信道相关矩阵，这个相关函数可用来计算平均功率为ϕ（0，0）的经典多普勒和指数多路径强度界面

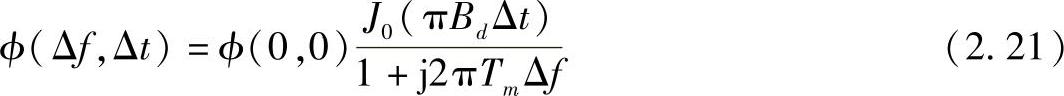
式中，B`_d与T_m分别为信道的多普勒扩展和多径扩展;J₀（·）为第一类一阶贝塞尔函数。

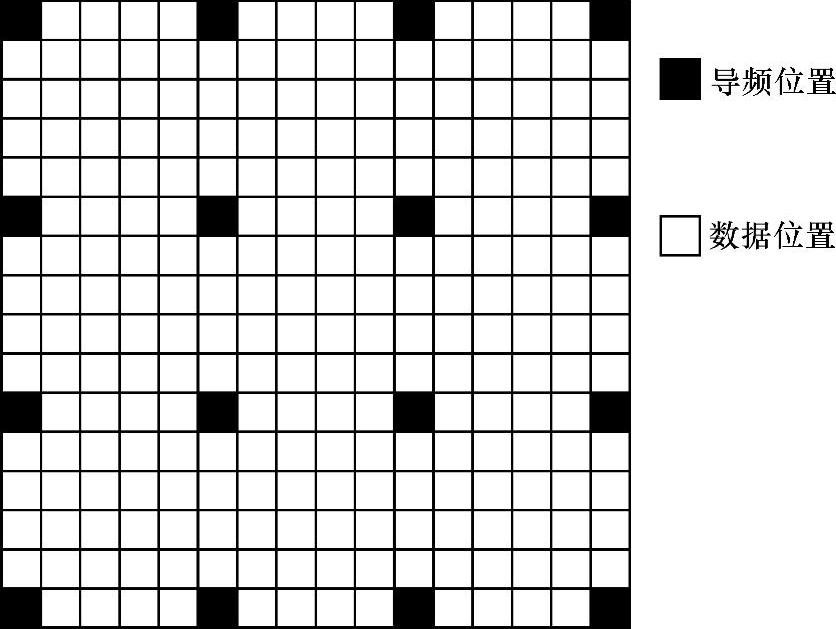
图2.8 时频块

接收端的第l个多样性分支接收到的信道可表述为

式中，｛B_k｝^N_k=-₀¹为等价离散信道协方差构成的N阶方阵F=E［C^lC^lH］的标准正交特征向量;｛G_k｝^N_k=-₀1为方差等于厄密矩阵F的特征值｛Γ_k｝^N_k=-₀1的独立复合零均值高斯随即变量。此矩阵的第（p，q）个入口由下式给出:

F_pq=ϕ｛［（m（p）-m（q）］Δf，［n（p）-n（q）］Δt｝ （2.23）

如图2.9所示，由空间非相关接收天线提供的L个分集支路组成了多载波接收机。

假定与符号a_mn相关的第l个多集输出信号可记为

R^l_mn=c^l_mnalmn+Nlmn （2.24）

式中，c^l_mn为第l个多集分支的离散信道增益因子;N^l_mn为方差为N₀的复合加性高斯白噪声。

图2.9 接收机框图

由以上的表达，我们可以得出基于最大后验概率（MAP）准则的信道估计器。｛G^l｝^l_l=^=L₀^-1的最大后验概率估计｛G＾^l｝^l_l=^=L₀^-1可定义为

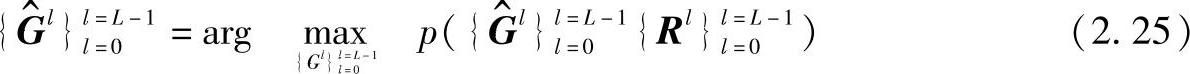
式中，｛R^l｝^l_l=⁼₀^L-1为L个多集支路上接收到的L个向量。

此方程可由最大期望算法（Expectation Maximisation Algorithm，EMA）迭代解出。第l个支路G^l（d+1）的第p个组成元可由下式给出:

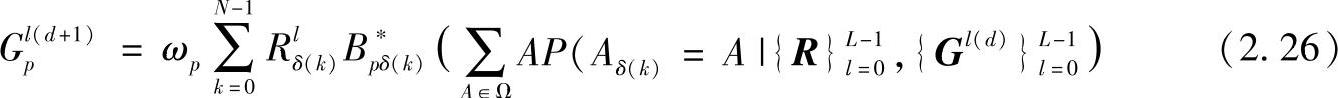
式中，B_p^∗_δ（k）为B_p的第k个组成元，并且

我们把

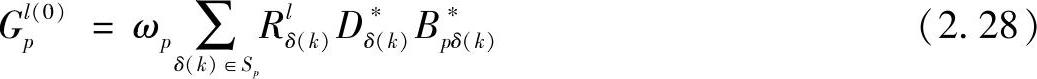
作为初始猜测值｛G｝^l（0）的第p个组成部分，式中D_δ（k）为信号点A_δ（k）确定的值，δ（k）∈S_p，S_p为在时-频块内的导频位置集合。

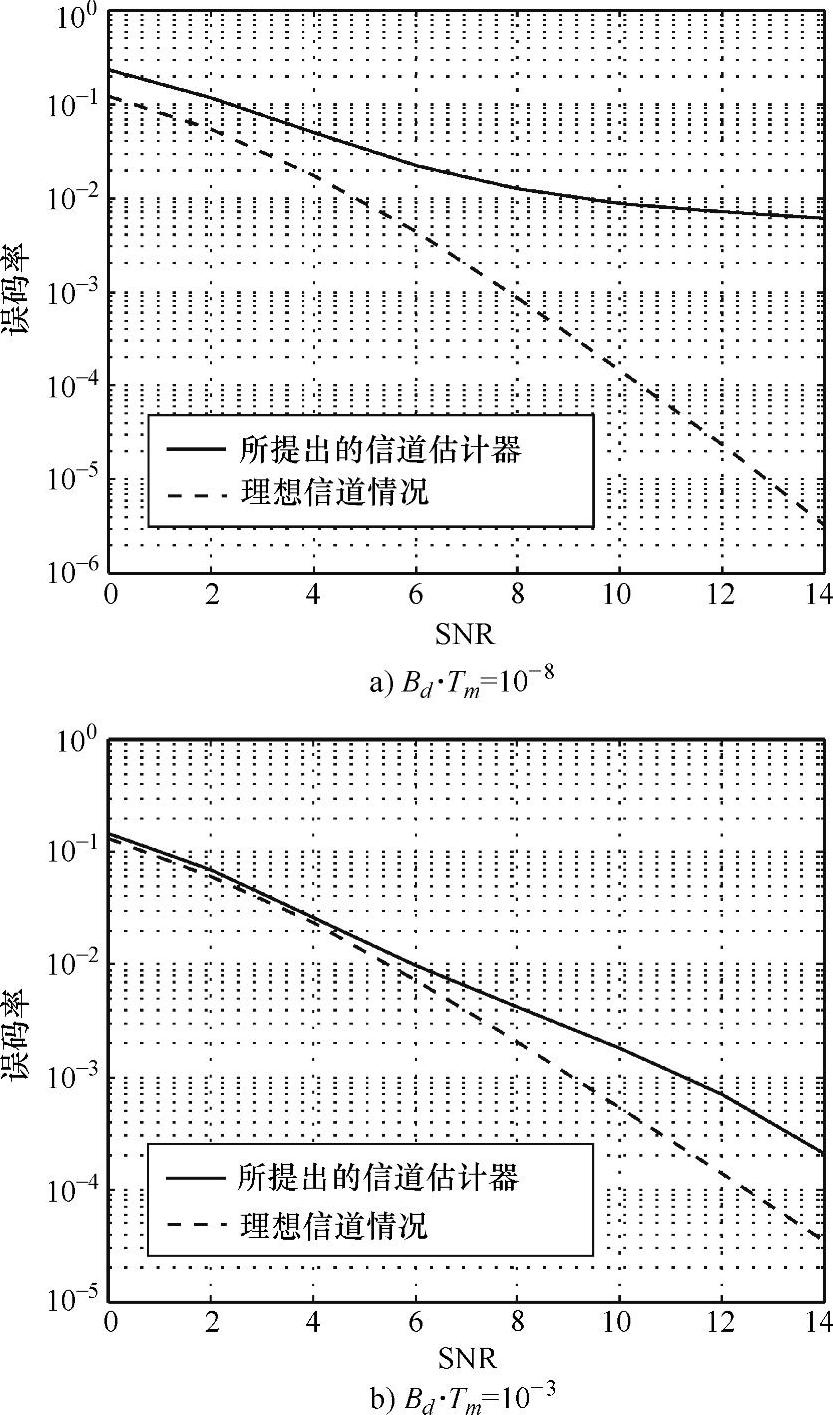
在极端选择性信道中，此方法表现出了非常好的性能，如图2.10所示。此外，解出MAP方程需要的迭代次数很少。用信道F的协方差矩阵的最强力的特征向量来表示信道可进一步降低复杂度。

(www.daowen.com)

图2.10 很高或者居中的时间频率选择性信道估计性能

2.联合信道估计

人们也研究了其他的技术，更直接地考虑多用户情况，如联合信道估计（JointChannel Estimation，JCE）。在参考文献［MWSL02］中记载了由Maniatis提出的针对这种可根据接收天线阵列形状进行的优化，如图2.11所示。

这个系统的每一个接入点（Access Point，AP）都装置有天线阵列。考虑阵列的特征，得到ML与最小均方误差（Minimum Mean Square Error，MMSE）联合信道估计的方程。ML估计可由下式给出:

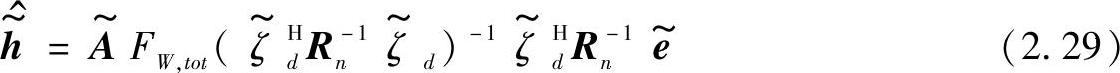
MMSE估计可由含有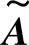、F_W，tot、R_hd、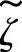_d、R_hd的式子给出:

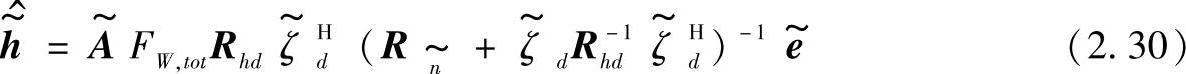
在JOINT的接收机处天线阵列的应用允许在设计移动终端（MT）和噪声信号的估计过程中包含有方向信息。联合利用频率关联与已知阵列的形状，ML-JCE的性能比起单接收机天线技术要好。应用最小均方误差估计原理，JCE的性能可以得到进一步改善，如图2.12所示。由于MMSE-JCE估计过程中包含有附加信道状态信息，所以性能要比ML-JCE的性能好些。不同于ML-JCE，MMSE-JCE不需要减少要进行估计的未知参数的数量。另一方面，MMSE-JCE需要知道所考虑的点对点无线信道的先验信息。

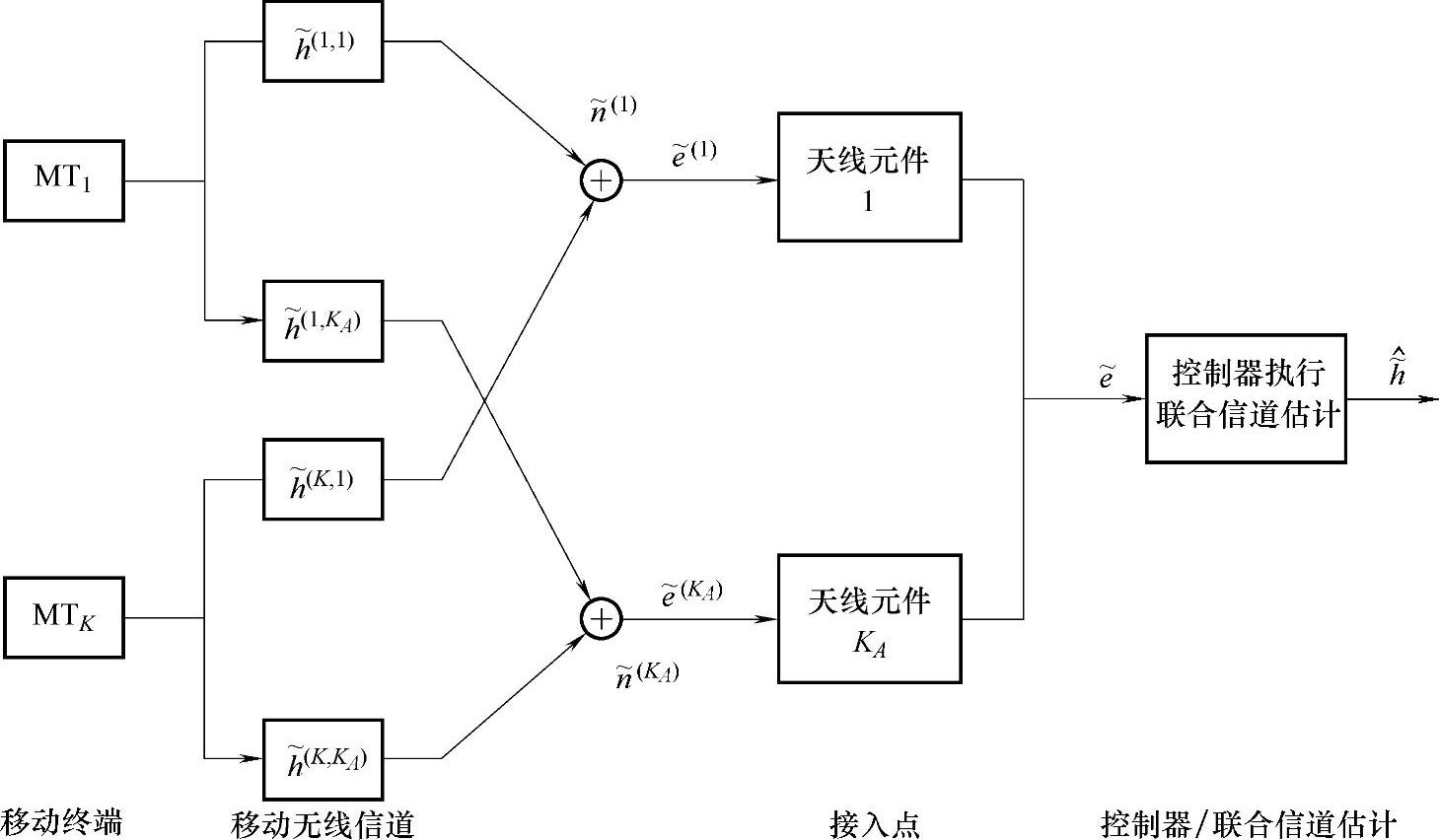
图2.11 在JOINT中用于上行链路信道估计的系统模型

3.比特与功率载荷

传统的OFDM系统在全部子信道上有固定的星座大小和功率等级分配。由于多径衰落，一些子信道的信噪比会严重下降，导致较高的总体误码率，我们常用编码来解决这一问题。如果信道是静态的（如在数字用户专线中）或者是缓慢时变的，接收机可以通过一个稳健的反馈信道将信道状态信息（Channel State Information，CSI）反馈给发射机。基于信道状态信息，一种自适应传输技术可以动态地修改调制器的参数，以达到改善性能的目的（见参考文献［KeHa00］）。

多载波调制，特别是OFDM，允许传输功率和每个子载波的比特率随信道选择性的变化（自适应比特载荷）而改变，这是它的优点之一。

比特载荷算法的首次，应用是在DSL系统中（见参考文献［Kale89］，［Bing00］）。

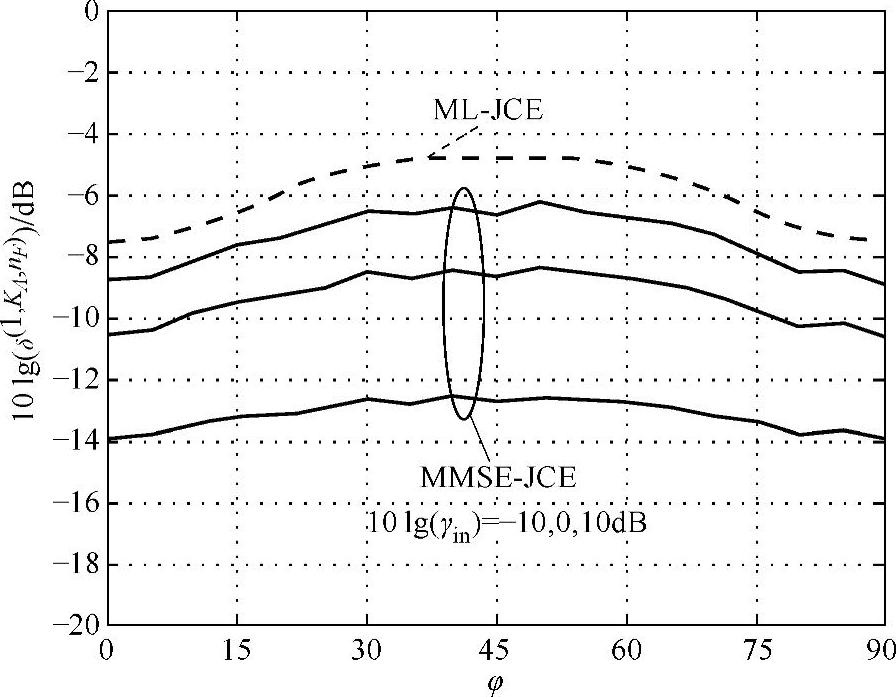
图2.12 不同φ值下的SINR（全方向噪声环境，K=4;K_A=4个接收天线元件）

众所周知，理论上信道容量可通过注水原理分配总传输能量得到。实际情况下，星座的大小需要有个确定的尺度，由注水原理得到的圆形比特分布并不是最佳方案。在异步数字用户线（Asynchronous Digital Subscriber Line，ADSL）的研究中提出了一些减轻复杂度的优化算法（见参考文献［ChCB95］，［FiHu96］）。Campello（见参考文献［Camp98］）给出了可以使离散比特分配达到理论上的最优条件。

近来，出现了一些研究自适应比特载荷算法在无线信道中应用的文章被发表（见参考文献［Czy196］，［PTVG98］，［BaFu01］，［DMMC02］）。既然这样，我们应该特别关注信道估计与信道状态信息刷新率对性能的影响（见参考文献［SuSc01］，［SoPi01］，［YeBC02］）。然而，基于注水原理的技术用于信道状态信息反馈的开销很大，这使得这些技术只适用于静态或者低速时变信道。此外，调制解调器必须能够不断地改变调制格式和基于子载波的功率（若数据传输速率高，则复杂度也越高）。

在参考文献［Dard04］中只是提到了选择最健壮的K个子信道（即具有较高增益的子信道）并通过保持总比特率与传输功率不变来达到的较大的星座尺寸。理想状态下，由于使用较大星座尺寸而损耗的功率可通过在较少的子信道上分配总功率来部分补偿。然而，人们希望的是最健壮的K个子信道的较高可靠性可以改善系统性能。

接收机的任务是估计信道的增益H_n，选择K个最健壮的（最可靠的）子信道，并通过反馈信道通知发射机哪些信道将用于下一次数据包传输。可以通过每T_csi秒传输一个分配掩码向量来完成上述过程，如图2.13所示，此向量中第n位是1表明第n个子信道可以使用。每个分配掩码向量中还可以加入循环冗余校验码（Cyclic RedundancyCheck，CRC）来检测误码。

图2.14描述了用于不同载荷配置下4-QAM和16-QAM系统的仿真结果。相应的有用数据传输速率分别为12Mbit/s和24Mbit/s。配置参数分别为K=N/2和K=2/3N时，两种系统的性能最好。由于排序方法的多样性，信噪比（Signal-Noise-Ratio，SNR）可以达到一个较高的值。图2.15所示，衰落与编码相关的12Mbit/s的系统中，平均数据包错误概率P_ep是E_b/N₀的函数。同时，K=N/2是最佳的载荷条件。在P_ep=10^-2时，相对于参考方案，获得的增益为6～7dB。

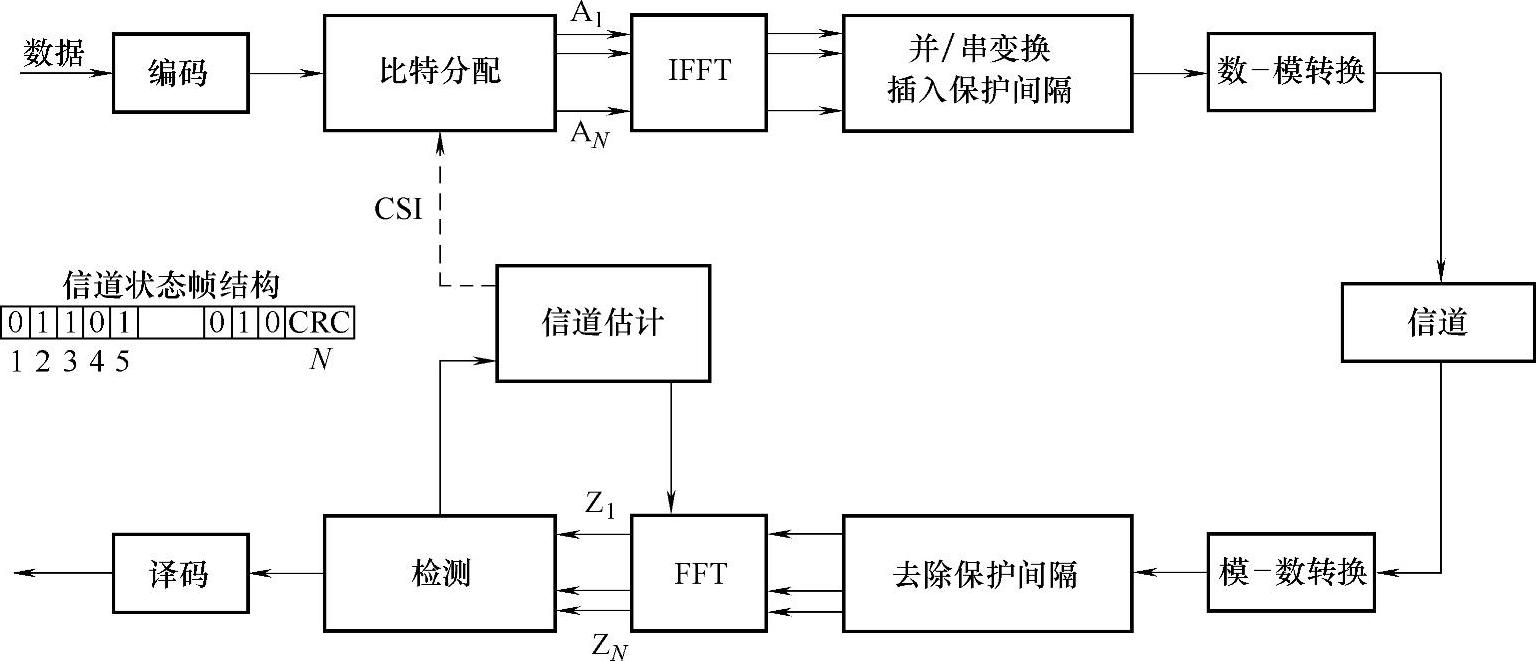
图2.13 传输系统框图

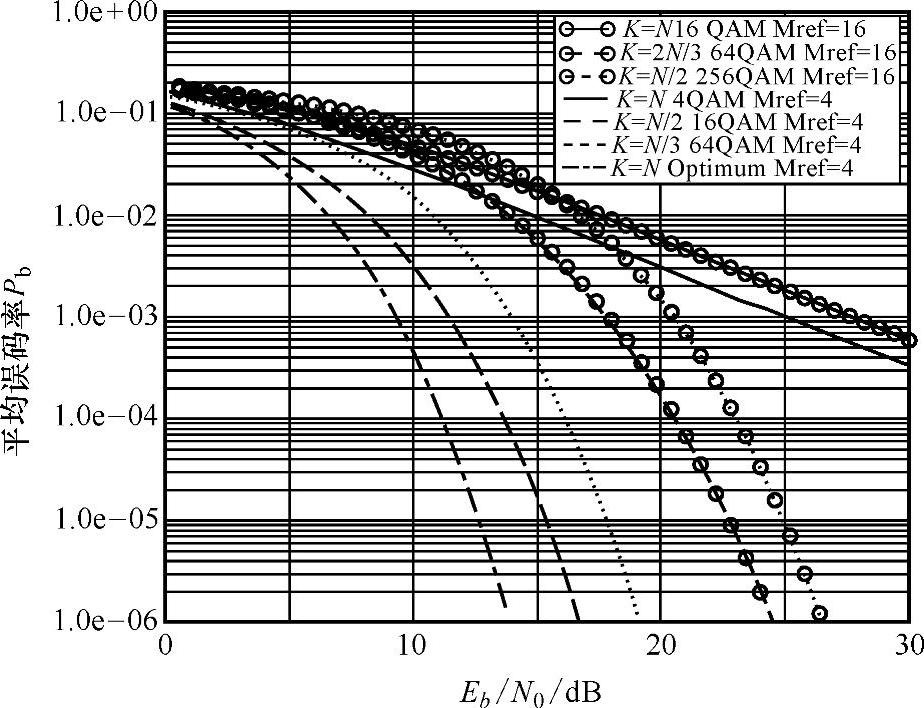
图2.14 在译码和独立的瑞利衰落仿真中平均误码率是E_b/N₀的函数

在同样的星座尺寸和功率级下，得到这些结果需要的硬件复杂度比得到最优解所需的硬件复杂度要低得多。

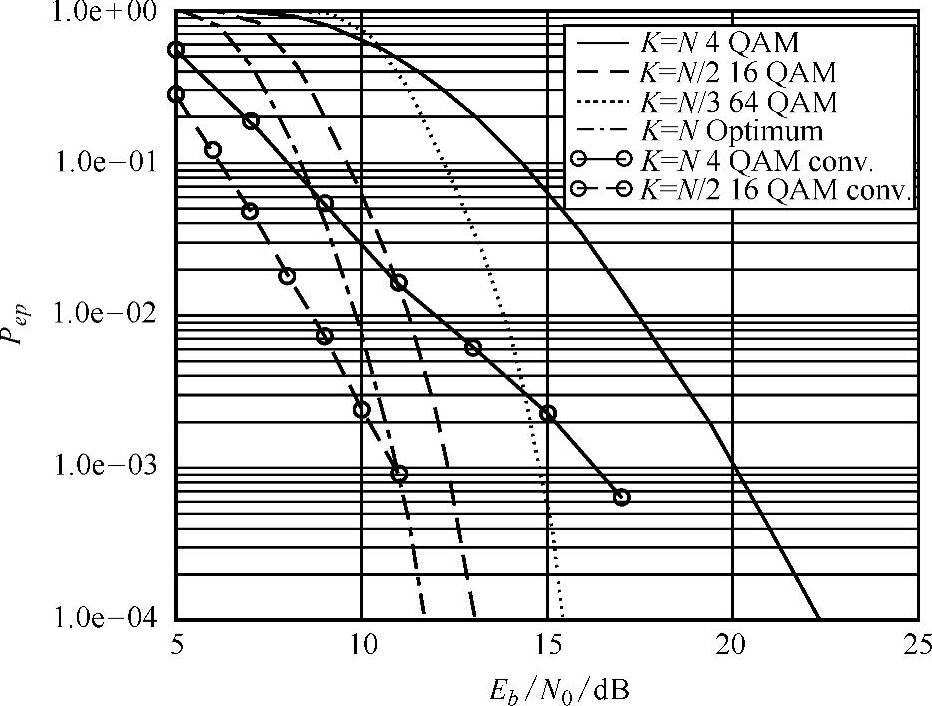
图2.15 平均数据包错误率作为E_b/N₀的函数

注:不同的负载条件:K=N，K=N/2和K=N/3，参考系统12Mbit/s。

曲线为用卷积码（软判决）仿真的结果。