由于OFDM可以应用保护间隔来简单缓解符号间干扰，所以对于频率选择信道来说，它是一种很有吸引力的调制方法。然而，OFDM一个众所周知的缺点是传输信号的时域波形显示为带有若干相对峰值的类高斯波形，这就很难在较大的动态范围内保证系统的线性行为。用来描述OFDM信号的非线性效应的一般性评估量为峰均功率比（Peak to Average Power Ratio，PAPR）。然而，这个评估量未必是表示OFDM信号的非线性效应最有代表性的参数。

1.减小峰均功率比

在如何减小OFDM信号的峰均功率比问题上，人们已经进行了很多研究。图2.2显示了在一般OFDM系统中峰均功率比的概率分布。

最经典的方法就是生成一个低峰均功率比的OFDM信号。为此，人们广泛研究了编码解决方案（见参考文献［WiJo95］，［Nee96］）和相移（见参考文献［Frie97］，［BaFH96］，［MuHu97b］，［Tell98］）。

另一个方法是人为地修改传输信号的振幅使之产生非线性失真（见参考文献［LiCi98］，［NeWi98］，［O.Lo94］，［DiWu98］，［WuGo99］），这种失真即使是使用纠错码（Error Correcting Code，ECC）（见参考文献［TeHC03］）的传统线性接收机也不能有效纠正。Kim和Stuber（见参考文献［KiSt99］）提出了一个迭代非线性解码器，即决辅助重建（Decision Aided Reconstruction，DAR），它可以纠正对OFDM传输的修改效应。这些先前的工作启发人们提出一个新算法，这种正在探索中的算法（见参考文献［GeCD04］）利用了当前高速率编码正交频分复用（Coded-OFDM，COFDM）技术中的纠错码。

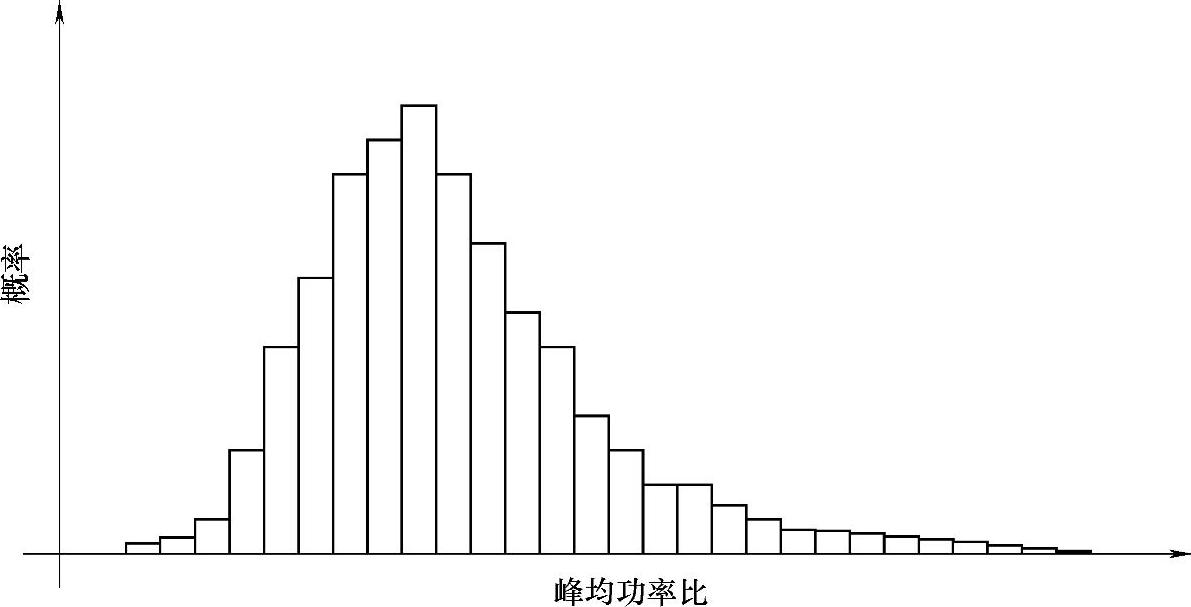
图2.2 峰均功率比的概率分布图

如图2.3所示，一个卷积二进制序列被映射到正交幅度调制（QAM）符号X上，并且在一个N点输出序列中通过快速傅里叶反变换对它进行了调制，如

式中，X为传输符号序列，X=｛X_k｝^N_k=-₀¹;N为OFDM块大小。

将一个保护间隔加入到X序列中，如下

x_k^G=x_k+N-G，0≤k≤N+G-1 （2.8）

式中，G为循环前缀的长度;（k）N为k模N的余数。

图2.3 Turbo-DAR传输系统

最后，对时间序列x^G进行分段后可表示为

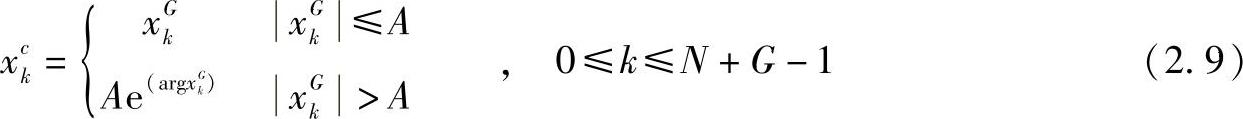
式中，x^c为分段后的输出的序列;A为分段幅度。

分段系数（CRa）定义为

式中，σ_x为x_k的标准差。

经信道传输并移除循环前缀后，信号可以记为

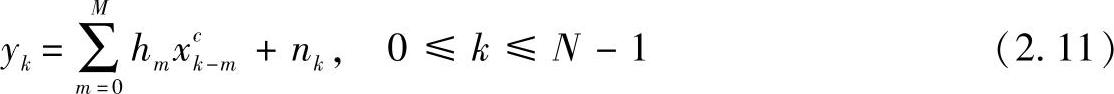
式中，h_m为以延时为m的信道系数;n_k为方差是N₀的零均值高斯白噪声。

将y_k进行快速傅里叶变换后，我们得到

Y_k=H_k·X^c_k+n_k

0≤k≤N-1 （2.12）

=H_k·X_k+Q_k （2.13）

式中，Q_k为高斯白噪声与分段后的噪声之和;H_k为第k个子载波的复合信道增益。

在频域使用迫零算法实现均衡:

均衡后的符号作为Turbo-DAR算法的输入。此算法的原理如图2.4所示，它使用了一种迭代技术，概括如下:

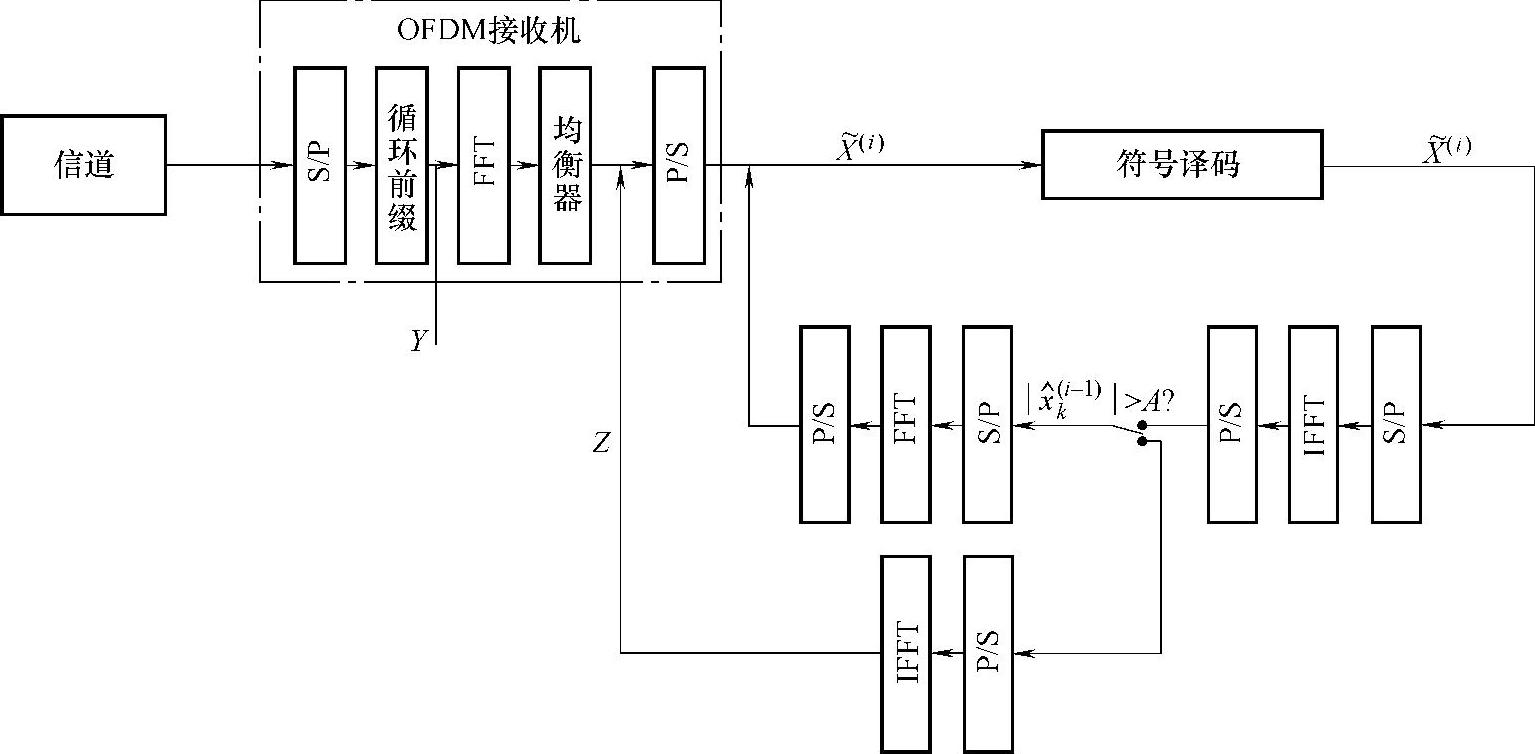
图2.4 Turbo-DAR算法原理图

1）首先，将均衡信号Z存储在内存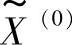=Z中。

2）使用硬件符号估计器对噪声符号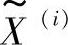进行编码，如图2.5所示。

使用如下的关系式将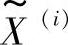软解映射:(www.daowen.com)

图2.5 Turbo-DAR硬符号译码原理

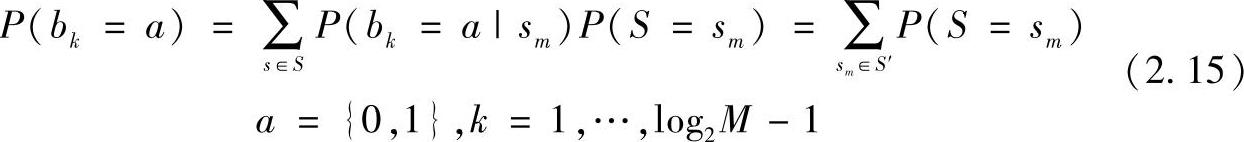
式中，S为M-QAM星座点的集合;S′为S的子集，如

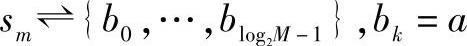
这些比特概率被交错以提供噪声码字比特P（C_k（i））的概率。把它作为维特比的输入来计算出最大概率译码序列C＾（i）和信息比特的估计值。

3）将C＾交错，映射到符号上，并用快速傅里叶变换反变换转换到时域中，得到。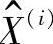

4）通过在时域中把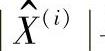与A做比较而实现对修正采样的检测:

5）通过快速傅里叶变换把估计符号转化到频域中。回到第二步，指针i+1。重复I次。

最后，通过维特比译码，用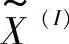得到估计信息比特来得到最终的判决，如图2.5所示。可以通过同样的方法来定义软决策Turbo-DAR，把维特比译码换为带有软输出Bahl-Cooke-Jelinek-Raviv（BCJR）译码即可。

图2.6阐明了我们提出的技术在CRa=1dB时，应用16-QAM的时不变频率选择性（Time Invariant Frequency Selective，TIFS）信道的性能。仿真结果显示通过结合应用纠错码与Turbo频域判决后，误码率（Bit Error Rate，BER）有极大改善。

尽管目前的结果是在平稳信道条件得出的，Turbo-DAR方法依然可用于时变信道，如带有适应性信道估计器的高速无线应用等（见参考文献［CiBi94］，［MoMe01］）。

2.额外功率:峰均功率比（PAPR）的替代者

似乎我们还尚未了解峰均功率比对非线性效应的影响（见参考文献［BeEr02］）。峰均功率比的减小总是会导致非线性效应的减小吗？

在一些最近的参考文献［Brai00］和［BSGS02］中，研究人员提出了一些其他的度量方法来测量非线性多载波系统的灵敏度。

一般来说，峰均功率比（PAPR）定义如下:

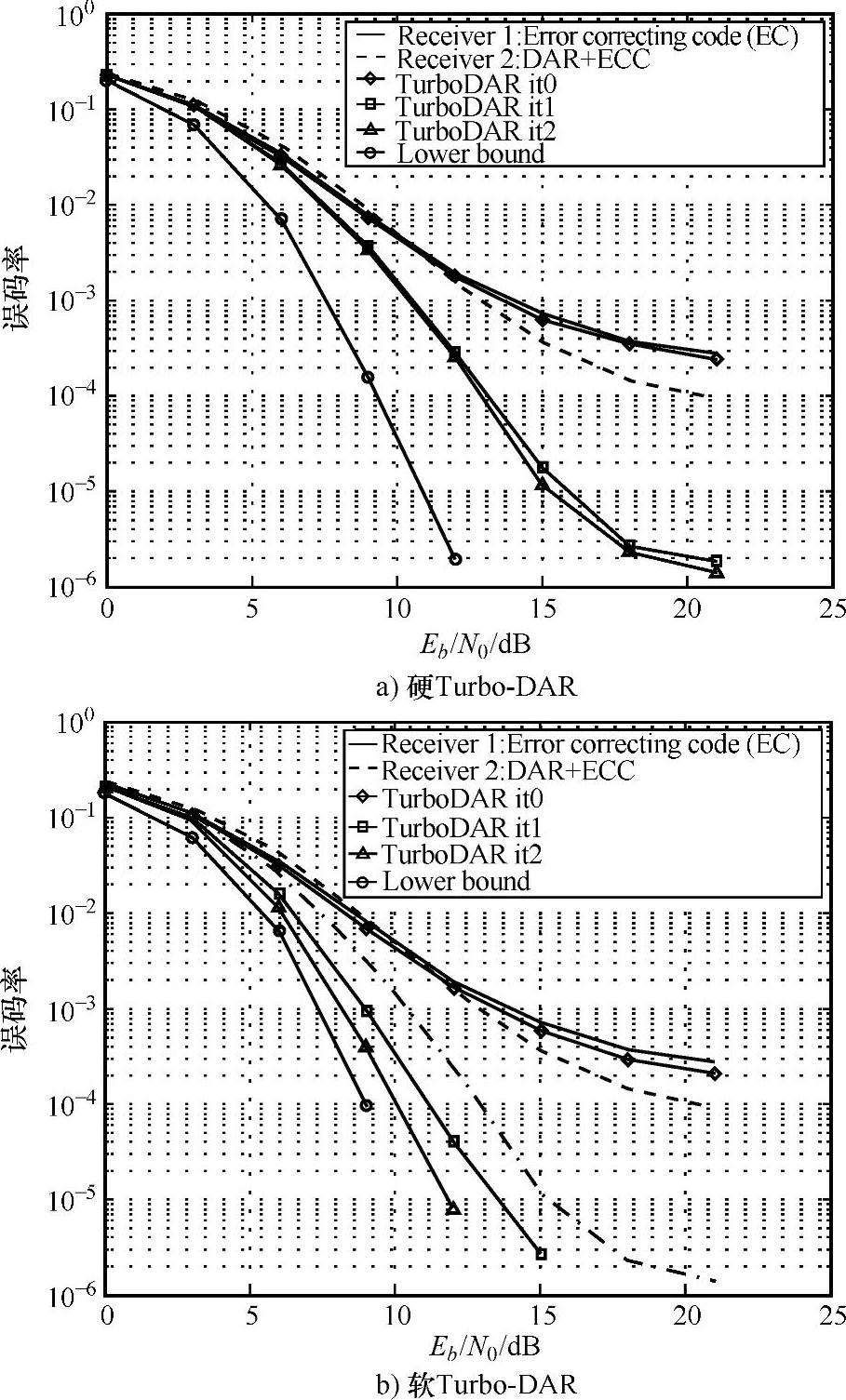
图2.6 在CRa=1dB时，应用16-QAM的时不变频率选择性信道， 硬软两种Turbo-DAR算法的误码率比较

理论上讲，OFDM符号的采样x_n的最大值可达N，但是达到这样的峰值的概率很小，尤其是在子载波很多的情况下更难达到。实际上，为了减小载波间干扰和带外辐射，需要让放大器工作在线性区域内。因此需要限制多载波信号的最大包络，即限制信号的峰均功率比。另一方面峰均功率比的减小并不意味着系统性能的改善。然而，我们在定义一种度量时还存在其他的可能。非线性信号衰落的度量方法应该具备的以下性质:

1）独立于非线性;

2）易于计算;

3）与非线性效应紧密相关。

第一个性质是必要的，因为在基带系统设计时，一般情况下系统的非线性操作点是未知的;当使用一组有限数据时，必须很容易就得出度量值，所以第二个性质也很重要;第三个性质显然也是很重要的。峰均功率比完全满足了第一个性质;离散信号的峰均功率比也完全满足第二个性质;然而，根据参考文献［Tala00］，非线性OFDM系统的性能取决于失真功率，信号的峰值不表示信号功率或失真功率。这就使峰均功率比不适用于某些应用。所以，我们定义超出一定功率的功率总量为OFDM符号的额外功率:

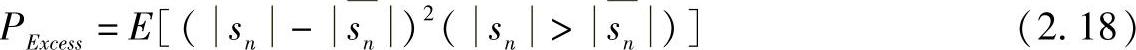
式中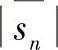，为信号的平均包络。

其可以表示振幅变化的度量有很多种，此定义只是其中之一。式（2.18）的更一般的形式为

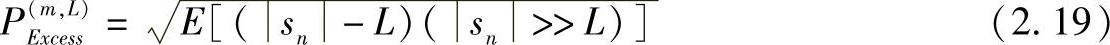
式中，L是失真的参考级。

当m=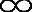时，L明确表示P_E（_xm_c，eL_ss）给出了信号的峰值。因此

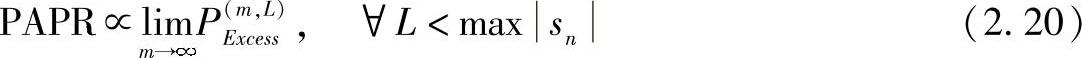
另一方面，如式（2.7）所示，当m=2时，P_E（m_xce，L_ss）成为功率的度量。峰均功率比和P_E（2_xc）ess两者都满足上述前两条性质。图2.7展示了失真功率与峰均功率比之间的相关系数，失真功率与额外功率的相关系数也在图中标出。此图说明，当非线性程度很高时，额外功率在表现失真上好一些，对于很高的补偿，峰均功率比更是一种很好的度量。

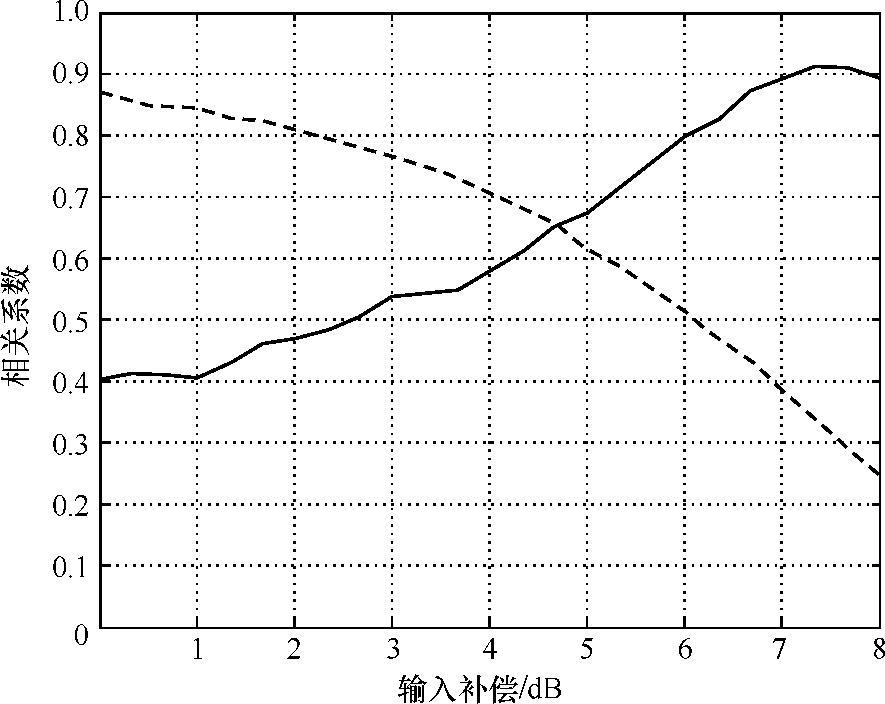
图2.7 对比不同的输入回退值，失真功率与峰均功率比之间的相关系数，失真功率与额外功率的相关系数