【摘要】:傅里叶分析是一种在频域中分析复周期信号的方法,可用于电路的进一步分析,还可观察在原信号中叠加其他信号的效果。傅里叶级数是将周期性的非正弦波信号,转换成直流成分基础上的正弦波或余弦波,即f=A0+A1cosωt+A2cos2ωt+…当用Multisim 进行离散傅里叶变换时,只使用电路输出端时域或瞬态响应基波成分的第二个周期来进行计算,第一周期认为是置位时间而丢弃。把图9-40电路的交流源用图9-44的电源代替,对修改后电路进行傅里叶分析。
傅里叶分析是一种在频域(FrequencyDomain)中分析复周期信号的方法,可用于电路的进一步分析,还可观察在原信号中叠加其他信号的效果。傅里叶级数是将周期性的非正弦波信号,转换成直流成分基础上的正弦波或余弦波(可能数量无限),即
f(t)=A0+A1cosωt+A2cos2ωt+…+B1sinωt+B2sin2ωt+…
当用Multisim 进行离散傅里叶变换时,只使用电路输出端时域或瞬态响应基波成分的第二个周期来进行计算,第一周期认为是置位时间而丢弃。每一谐波的系数由时域中从周期的开始到时间t这段时间内采集到的数据计算而来,一般来说是自动设定的,且是基本频率的一个函数。傅里叶分析需要设定一个基本频率,使它与交流源的频率相匹配,或者是多个交流源频率的最小公因数。
把图9-40电路的交流源用图9-44的电源代替,对修改后电路进行傅里叶分析。基本频率和停止时间均点击“Estimate”按钮由程序设定,基频值最后选定为20Hz(对于多个交流源,取它们频率的最小公因数);谐波数设为9;结果显示选择显示相位图,显示方式为线形图,并对图形归一化;以图和表的形式显示;纵坐标选择线性坐标。点击仿真按钮,可得图9-45的仿真结果。(https://www.daowen.com)
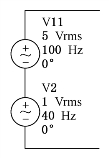
图9-44 多交流源电路

图9-45 仿真结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






