在电子计算机和数字系统中，使用最多的时序电路是计数器。计数器的用途非常广泛，它不仅能用于对时钟脉冲计数，还可以用作分频、定时、产生节拍脉冲和进行数字运算等。计数器的种类繁多，按计数器中的各个触发器翻转的先后次序分类，可以把计数器分为同步计数器和异步计数器；按计数过程中数字的增减分类，可分为加法计数器、减法计数器；按计数器循环模数（进制数）不同，又可分为二进制计数器、十进制计数器和任意进制计数器。

1.二进制计数器

二进制只有0和1两个数符，而一个触发器具有0和1两种状态，因此可以用一个触发器表示一位二进制数，用n个触发器连接起来，就可以表示n 位二进制数，从而构成n位二进制计数器。

（1）异步二进制计数器

如图8-15所示为四位异步二进制加法计数器逻辑图，它是由4个JK 触发器所组成，并且四个触发器的输入端均为1，即J＝K＝1。计数脉冲从最低位触发器F0 的CP端输入。每输入一个计数脉冲，F0 的状态改变一次。低位触发器的端与相邻高位触发器的CP 端相连，每当低位触发器状态由1翻转为0时，Q端输出一个由0变l的正跳变信号，使高位触发器翻转。这种计数器的计数脉冲不是同时加到各触发器的计数输入端，而只加到最低位触发器的计数输入端，其他各级触发器则由相邻的低位触发器输出的进位信号来触发，故称为异步计数器，它具有串行触发的特点，又称为串行计数器。

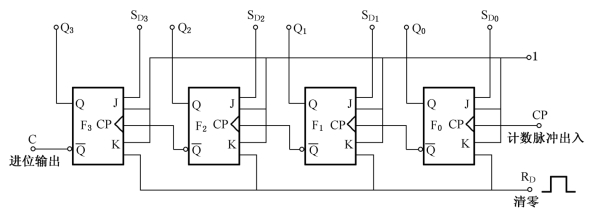
图8-15　四位异步二进制加法计数器逻辑图

设计数器原状态为0000，当第1个计数脉冲输入后，F0 的Q0 由0变为1，未产生进位信号，故F3、F2、F1 保持0状态，计数器的状态为0001；当第2个计数脉冲输入后，F0 的Q0 由1变为0， 产生一个正阶跃信号作用至F1 的CP端，使F1 的Q1 由0变1，而此时F3、F2 仍保持0状态，计数器的状态为0010；依此类推。当第15个计数脉冲输入后，计数器的状态为1111，第16个计数脉冲输入，计数器的状态返回到0000。

由上述分析可知，一个四位二进制加法计数器有24＝16种状态，每输入16个计数脉冲，计数器的状态就循环一次，故又称其为一位十六进制加法计数器。

图8-16是四位二进制加法计数器的工作波形图。根据分析还可列出四位二进制加法计数器的状态转换表，如表8-6所示。

图8-16　四位二进制加法计数器的工作波形

表8-6　四位二进制加法计数器状态转换表

由图8-16的波形图还可以看出，每经过一级触发器，脉冲周期增加1倍，即频率降为原来的1/2。于是从Q0 端引出的波形为二分频，从Q1 端引出的波形为四分频，依此类推。从Qn＋1端引出的波形为2n＋1分频，因此计数器可以用来作分频电路。

综上所述，异步二进制加法计数器有如下特点：

1）计数器的计数规律符合二进制加法运算规则：0＋1＝1；1＋1＝0，使本位为0，向高位进1。

2）计数器中各位触发器的连接方式由触发器的类型而定，如用脉冲上升沿触发的触发器构成的计数器，进位信号从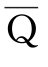 端引出；如用脉冲下降沿触发的触发器构成的计数器，进位信号从Q 端引出。

3）计数器所能累计的最大脉冲数称为计数容量N，一个四位二进制加法计数器能累计的最大脉冲数N＝24－1＝15。同理，一个n 位二进制加法计数器具有2n 个状态，其计数容量为N＝2n－1。

4）计数器可以通过SD0～SD3预置被加数，若计数从0000 开始时，它们应接地。

如图8-17所示为4位异步二进制减法计数器逻辑图。它由4个JK 触发器按二进制减法规则连接。根据二进制减法规则，若低位触发器原状态为0，则输入一个减法计数脉冲，应翻转为1，同时向高位发出借位信号，使高触发器位翻转。即计数规律应符合二进制减法运算法则，1－1＝0；0－1＝1，使本位为l，向高位借1。

图8-17　四位异步二进制减法计数器

仿照前述加法计数器的分析方法，读者可自行分析该减法计数器的逻辑功能和状态转换表。

（2）同步二进制计数器

同步二进制计数器是利用计数脉冲同时触发计数器中各位触发器的CP端，各位触发器的状态转换与计数脉冲同步。

图8-18是由4个JK 触发器组成的四位同步二进制加法计数器的逻辑图，各位触发器受同一个计数脉冲触发，按各自不同的输入条件翻转。

图8-18　四位同步二进制加法计数器

由图8-18可得出各位触发器的J、K 端的逻辑关系式：

J0＝K0＝1，J1＝K1＝Q0，J2＝K2＝Q1Q0，J3＝K3＝Q2Q1Q0

其工作过程分析如下：设计数器原状态为0000。第1个计数脉冲到来后，F0翻转为1态，由于此时F1、F2、F3 的输入均为0，故不翻转，计数器输出状态为0001；第2个计数脉冲到来前，由于F1 的输入J1＝K1＝Q0＝1，故在第2个计数脉冲到来后，F0 由1翻转为0，F1 由0翻转为1，而此时F2、F3 的输入均为0，不翻转。计数器输出状态为0010；依此类推，直到第15个计数脉冲到来，计数器输出状态为1111，第l6个计数脉冲到来，由于各位触发器均满足翻转条件，全部翻转为0，故计数器返回0000状态。

2.十进制计数器

二进制计数器结构简单，分析设计都较容易，但人们对二进制数毕竟不如常用的十进制数那样熟悉，特别是当二进制的位数较多时，要很快读出数来就比较困难，尤其是输出具有数码显示功能的场合，常采用十进制计数器。

如图8-19所示为由四位JK 触发器组成的同步十进制加法计数器逻辑图。

图8-19　同步十进制加法计数器逻辑图

同步十进制计数器的计数脉冲同时加到各位触发器的CP端，各位触发器是否翻转，要看触发器的输入状态是否满足翻转条件，通常采用时序电路的一般分析方法，即通过特征方程分析其逻辑功能。

由图8-19可写出各位触发器输入端的激励方程为

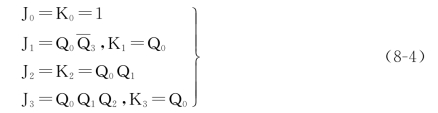
将式（8-4）代入JK 触发器的特征方程式（8-2）即得计数器特征方程为

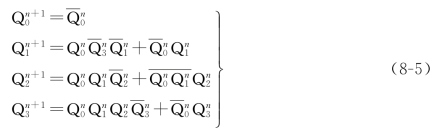(www.daowen.com)

进位输出端

设计数器初始状态为0000，则根据式（8-4）、式（8-5）计算出计数器的状态转换表如表8-7所示。

表8-7　异步十进制加法计数器状态表

计数器计数到Q3Q2Q1Q0＝1001时，再来一个计数脉冲，F0 和F3 由1翻转为0，F1 和F2 保持0不变，计数器状态为0000，完成一位十进制计数。同时进位输出端C＝Q3Q0＝1，实现本位归0向高位进1的进位规则。

该计数器的各位触发器是由CP脉冲的上升沿触发的，其工作波形如图8-20所示。

图8-20　同步十进制加法计数器工作波形

3.任意进制计数器

除二-十进制计数器外，还有三、四、五、六、七等其他进制的计数器。如前所述，一位触发器即构成一位二进制计数器；二位触发器可构成二位二进制计数器，也是一位四进制计数器，在其中引入适当的反馈线可构成一位三进制计数器；三位触发器可构成三位二进制计数器，也是一位八进制计数器，在其中引入适当反馈线可构成一位五、六、七进制计数器……

例8-3 电路如图8-21所示，试分析其逻辑功能。

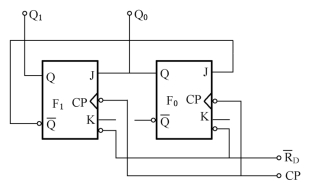
图8-21　例8-3图

解 这是一个同步计数器。由图可见，激励方程为：J0＝，K0＝1，J1＝Q0，K1＝1，将它们代入JK 触发器的特征方程得

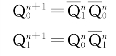
设计数器原状态为Q1Q0＝00，第一个计数脉冲到来后，由0变1，不变；计数器输出为Q1Q0＝01；第二个计数脉冲到来后，由1变为0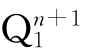，则由0变为1，计数器输出为Q1Q0＝10；第三个计数脉冲到来后，＝0，＝0，计数器回到0状态。可见，该计数器为三进制加法计数器。表8-8为其状态转换表。

表8-8　三进制加法计数器状态转换表

图8-22为同步五进制加法计数器的逻辑图，读者可自行分析其逻辑功能。

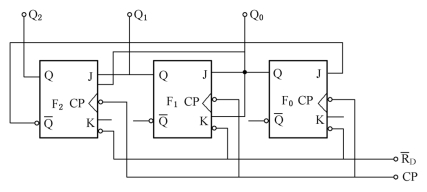
图8-22　同步五进制加法计数器

如图8-23所示为集成电路二-五-十进制计数器74LS290的管脚功能图和功能表。R0（1）和R0（2）是清零输入端，当它们为1时，计数器将被清零，Q3Q2Q1Q0＝0000；S9（1）和S9（2）是置9输入端，当它们为1时，计数器被置为9，Q3Q2Q1Q0＝1001。由功能表可见，清零时S9（1）和S9（2）中至少有一端为0，以保证清零可靠进行。它有两个时钟脉冲输入端，用来控制进位制的转换。

图8-23　74LS290型计数器

（1）只输入计数脉冲CP0，由Q0 端输出，Q1～Q3 不用，为二进制计数器。

（2）只输入计数脉冲CP1，由Q3、Q2、Q1 端输出，为五进制计数器。

（3）将Q0 端与CP1 端相连，在CP0 端加计数脉冲，则可得到8421码的十进制计数器。

如将计数器适当改接，利用其清零端进行反馈置0，可得到小于原进制的多种进制的计数器。例如将图8-23a中的8421码十进制计数器改接成如图8-24所示的两个电路，就分别成为六进制和九进制计数器。

图8-24　74LS290改接为六、九进制计数器

例8-4 数字钟表中的分、秒计数都是六十进制，试用两片74LS290型二-五-十进制计数器连成六十进制电路。

解 六十进制计数器由两位组成，个位F1 为十进制，十位F2 为六进制，电路连接如图8-25所示。个位的最高位Q3 连到十位的CP0 端。

图8-25　例8-4图

个位十进制计数器经过十个脉冲循环一次，每当第十个脉冲来到后，Q3 由1变为0（见表8-7），相当于一个下降沿，使十位的六进制计数器计数。个位计数器经过第一次十个脉冲，十位计数器计数为“0001”；经过二十个脉冲，计数为“0010”；依此类推，经过六十个脉冲，计数为“0110”。接着，立即清零，个位和十位计数器都恢复为“0000”。这就是六十进制计数器。

[思考题]

1.说明时序逻辑电路和组合逻辑电路在逻辑功能上和电路结构上有何不同。

2.数码寄存器和移位寄存器有什么区别？

3.n位的二进制加法计数器，能计数的最大十进制数是多少？ 如果要计数的十进制数为100，需要几位的二进制加法计数器？

4.异步计数器和同步计数器有何不同？ 二进制计数器和十进制计数器有何不同？

5.试用两片74LS290构成百进制计数器。