1.编码

不同的数码不仅可以表示数量的不同大小，而且还能用来表示不同的事物或一些文字符号信息，此时该数码称为代码。例如，在举行长跑比赛时，为便于识别运动员，给每个运动员编一个数码，显然，这些不同的数码，仅代表不同的运动员，而失去了数量大小的含义。

把若干个二进制数码0和1按一定规律编排在一起，组成不同的代码，并且赋予每组代码以特定的含义，叫做编码。为了便于记忆和查找，在编制代码时，要遵循一定的规则，这些规则称为码制。

（1）二进制编码

用二进制代码表示有关对象（文字符号信息）的过程叫做二进制编码。在数字电路中大量使用的是二进制编码，因为二进制代码只有0、1两个数符，电路上实现起来最容易。1位二进制代码有0、1两种状态，可以表示两个不同的信息；两位二进制代码有00、01、10、11四种组合，可以表示四个不同的信息。一般地说，n 位二进制代码有2n 种组合，可以表示2n 个不同的信息。所以，对N 个信息进行编码时，可用公式2n≥N 来确定需要使用的二进制代码的位数n。

（2）二-十进制编码

用二进制数的形式表示十进制数的编码称为十进制数的二进制编码，简称二-十进制编码，也称BCD 码。

二-十进制编码是用四位二进制数表示一位十进制数符的编码方式。由于四位二进制数有16种（24＝16）不同的组合，而十进制数的10个数符只需要其中的10种组合。根据代码排列的规律，共有N＝＝16×（16－1）×（16－2）×…×[16－（10－1）]≈2.9×1010种方案可供选择。不同的选择方案就形成不同的BCD 码。常用的BCD 代码如表7-16所示。

二-十进制码种类繁多，大致可分为有权码和无权码两大类。表7-16中的前四种为有权码，即每位都对应着一个固定的位权值。如8421BCD 码，自高位到低位，各位的位权值为23222120，即8421。如果将每个代码看作一个四位二进制数，那么这二进制数的值恰好对应着它所代表的十进制数的大小。因此这种代码命名为8421BCD 码。这是一种最基本的BCD 码，使用起来简便自然，应用较为广泛。

表7-16　常用BCD码

例7-16 用8421BCD 码表示十进制数468。

解 4 6 8

↓ ↓ ↓

010001101000

所以，（468）10＝（010001101000）8421BCD

值得注意的是，每四位BCD 码表示一位十进制数，因此，BCD 码前面的“0”不可以省略。

2.编码器

用以完成编码的数字电路，称之为编码器。

（1）二进制编码器

用n 位二进制代码对N＝2n 个一般信号进行编码的逻辑装置，叫作二进制编码器。如图7-41所示是三位二进制编码器。(www.daowen.com)

图7-41　三位二进制编码器

分析编码器的逻辑功能，可以用组合电路的分析方法，即先根据逻辑图写出输出的逻辑表达式，再写出真值表，进而得出其逻辑功能。

根据图7-41可列出各输出的逻辑表达式：

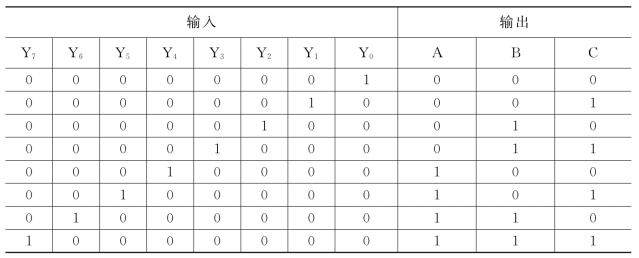
编码器某一时刻只能对一个输入信号进行编码，即在输入端不允许两个或两个以上信号为1的情况。由此可写出如表7-17所示的真值表（也叫编码表）。

表7-17　3位二进制编码器的真值表

要设计一个二进制编码器，首先应分析设计要求，然后列出真值表（编码表），根据真值表写出简化的输出函数表达式，最后画出逻辑图。应该指出的是，二进制编码的方式不是唯一的，因此，实现二进制编码的电路也不是唯一的。

（2）键控8421BCD 码编码器

因为计算机只能识别二进制代码，而人们习惯于十进制数，因此，在向计算机输入数据时，需要进行十进制数向二进制数的转换，键控8421BCD 码编码器就可完成此任务。计算机的键盘输入逻辑电路就是由这种编码器组成的。

图7-42是由10个按键和门电路组成的8421码编码器。其中S0～S9 代表10个按键，同时作为输入逻辑变量，ABCD 为代码输出（A 为最高位）。

图7-42　键控8421码编码器原理电路

当按下某一按键，如按下S3 时，则S3＝0，其余均为1，这时ABCD＝0011。同理，当按下不同按键时，便得到相应的输出代码。由此可列出键控8421码编码器的真值表，如表7-18所示。

表7-18　8421码编码器真值表

续表7-18

由表7-18可见，不论是否按下S0 键，ABCD 都位0000，为了区分S0 键是否被按下，设置了S输出端，称为控制使用标志。当按下S0～S9 中任一键时，S均为1，不按键时，S为0。这样，可以利用控制使用标志S的高、低电平来判断S0键是否被按下。