1.反相加法运算电路

在如图6-6所示电路的基础上，反相输入端增加若干个输入回路，可以方便地实现对几个输入电压的代数相加运算，称为反相加法运算电路。如图6-9所示为具有三个输入电压的反相加法运算电路。

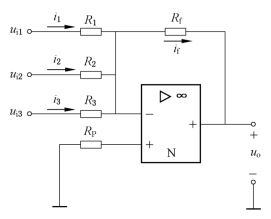
图6-9　反相加法运算电路

根据“虚短”的特点，由图可列出：

u－≈u＋＝0

在反相输入端可列出

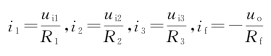
又由“虚断”的特点

i1＋i2＋i3＝if

得输出电压为

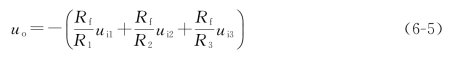
式（6-5）说明，输出电压等于全部输入电压按比例相加，且极性相反，故该电路称为反相加法运算电路。

反相加法运算电路的实质是通过电流相加的方法实现电压相加。该电路可以推广到有n 个输入电压的求和运算。运算结果也表明，uo 和ui 的关系与集成运放本身的参数没有关系，只与外部连接电阻的方式和参数有关，只要电阻R1、R2、R3、Rf 足够精确，该电路就能保证反相加法运算的精确度和稳定性。

当R1＝R2＝R3＝Rf 时，有

式（6-6）表明，该电路能够实现多个输入电压的加法运算。

平衡电阻RP＝R1∥R2∥R3∥Rf。

例6-1 两级运算放大器应用的实例。在如图6-10所示电路中，已知ui1＝1V，ui2＝0.5V，求输出电压uo。

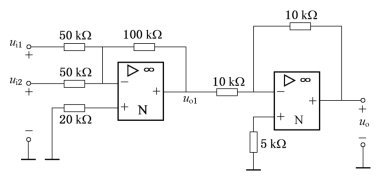
图6-10　两级运算放大器电路

解 本电路由两级运算电路串联而成，第一级为反相加法运算电路，第二级为反相器，其输入信号为前级运算电路的输出信号uo1。

第一级输出电压为

(www.daowen.com)

第二级输出电压为

2.同相加法运算电路

在图6-7的电路中，若在同相输入端增加若干个输入回路，可以实现对多个输入电压的代数相加运算，称为同相加法运算电路。如图6-11所示电路是具有两个输入电压的同相加法运算电路。图中外部的元件参数应满足关系式R2∥R3＝Rf∥R1。

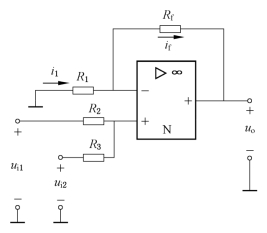
图6-11　同相加法运算电路

应用叠加原理可知，u＋可由ui1和ui2两个电压源单独作用的叠加求出：

ui1 单独作用时，令ui2＝0，u′＋＝。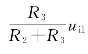

ui2单独作用时，ui1＝0，u″＋＝。

两个电压源共同作用时，u＋＝u′＋＋u″＋＝。

根据“虚短”现象，u－≈u＋，而u－＝，所以有输出电压为

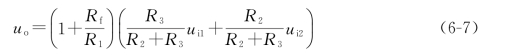
若选取R1＝R2＝R3＝Rf，则式（6-7）可写成下式：

本电路可以推广到同相输入端接有n 个输入电压的加法运算电路。但是，电路外接电阻的选择，以及要满足电阻平衡和比例系数的要求，使该电路的设计比较麻烦。

例6-2 如图6-12所示电路为两输入信号的同相加法运算电路，试求输出电压和两个输入电压的关 系。若R1＝R2＝R3＝6kΩ，R4＝Rf＝3kΩ，ui1＝5mV，ui2＝10mV，求输出电压uo。

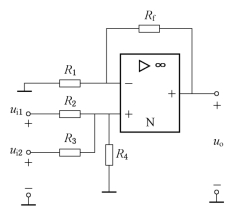
图6-12　例6-2图

解 由“虚断”特点，得

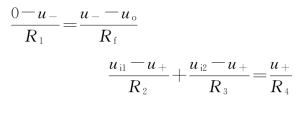
由“虚短”特点，得

u－＝u＋

代入数据，由以上几式解得

uo＝5.625mV