如图4-9所示的是变压器的原理图。为了便于分析，我们将高压绕组和低压绕组分别画在两边。与电源相连的称为一次绕组（或原边绕组），与负载相连的称为二次绕组（或副边绕组）。一次、二次绕组的匝数分别为N1 和N2。

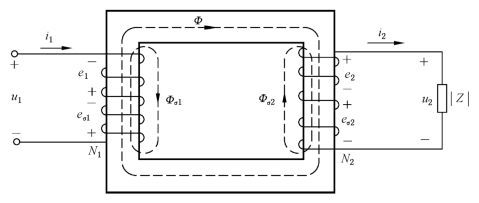
图4-9　变压器的原理图

当一次绕组接上交流电压u1 时，一次绕组中便有电流i1 通过。一次绕组的磁动势N1i1 产生的磁通绝大部分通过铁心而闭合，从而在二次绕组中感应出电动势。如果二次绕组接有负载，那么二次绕组中就有电流i2 通过。二次绕组的磁动势N2i2 也产生磁通，其绝大部分也通过铁心而闭合。因此，铁心中的磁通是一个由一次、二次绕组的磁动势共同产生的合成磁通，它称为主磁通，用Φ 表示。主磁通穿过一次绕组和二次绕组而在其中感应出的电动势分别为e1 和e2。此外，一次、二次绕组的磁动势还分别产生漏磁通Φσ1和Φσ2，漏磁通仅与各自绕组相交链，从而在各自的绕组中分别产生漏磁电动势eσ1和eσ2。

下面分别讨论变压器的电压变换、电流变换及阻抗变换。

1.电压变换

根据基尔霍夫电压定律，对一次绕组电路可列出电压方程

通常原绕组上所加的是正弦电压u1，则在正弦电压作用的情况下，上式可用相量表示为

式中，R1 为一次绕组的电阻；X1＝ωLσ1为一次绕组的感抗，即漏磁感抗，是由漏磁通产生的。

由于原绕组的电阻R1 和感抗X1 较小，因而它们两端的电压降也较小，与主磁电动势e1 比较起来可以忽略不计，则有

感应电动势e1 的有效值为

同理，对二次绕组电路可列出电压方程

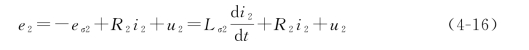
式（4-16）可用相量表示为

式中，R2 为二次绕组的电阻；X2＝ωLσ2为二次绕组的感抗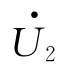； 为二次绕组的端电压。

感应电动势e2 的有效值为

在变压器空载时，由于I2＝0，则

式中，U20是空载时二次绕组的端电压。

从式（4-15）、（4-18）和（4-19）可得出一次绕组的电压与二次绕组的电压之比

式中，K 称为变压器的变比，亦即一次、二次绕组的匝数比。

由上式可见，由于一次、二次绕组的匝效N1 和N2 不相等，故E1 和E2 的大小是不等的，因此输入电压U1 和输出电压U20的大小也是不等的。当输入电压，即电源电压一定时，只要适当选取一次、二次绕组的匝数，就可将电源电压变为所需要的不同的输出电压值。

2.电流变换

由式（4-15）可见，当电源电压U1 和频率f 不变时，Φm 也近于常数，这说明，铁心中主磁通的最大值在变压器空载或有载时是基本恒定的，即铁心中的主磁通几乎与负载无关。因此，有载时产生主磁通的一次、二次绕组的合成磁动势N1i1＋N2i2 应该和空载时产生主磁通的一次绕组的磁动势N1i0 近似相等，即

上式用相量表示为

(www.daowen.com)

变压器的空载电流i0 是励磁电流，其值很小，常可忽略。于是式（4-22）可写成

由上式可知，一次、二次绕组的电流关系为

其有效值之比为

式（4-25）表明变压器一次、二次绕组的电流之比近似等于它们的匝数比的倒数。这是变压器的另一个基本关系，它反映了变压器具有电流变换的功能。变压器一次、二次绕组之间虽无直接的电的联系，但它们之间存在磁的耦合，而使一次绕组电流随二次绕组电流变化。

变压器的额定电流I1N和I2N是指按规定工作方式（长时连续工作或短时工作或间歇工作）运行时一次、二次绕组允许通过的最大电流，它们是根据绝缘材料允许的温度确定的。二次绕组的额定电压与额定电流的乘积称为变压器的额定容量（视在功率），即

变压器除能起变换电压和变换电流的作用外，它还有变换负载阻抗的作用，以实现阻抗匹配。

3.阻抗变换

根据上述一次、二次绕组电压、电流的关系，可以得出

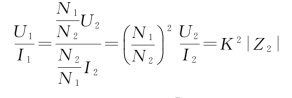
令

则

式中，Z1 是一次绕组等效阻抗，或者称为变压器转移阻抗，即负载阻抗通过变压器转移到其输入端口的等效阻抗。

变压器的这种阻抗变换作用，常用于电子线路的功率放大级中，使负载（如扬声器）能获得较大的功率。

由式（4-17）可以看出，当电源电压U1 不变时，变压器负载后，二次绕组电压U2 将随二次绕组电流I2 的变化而有所变化。当电源电压U1 和负载功率因数cosφ2 为常数时，U2 随I2 的变化关系如图4-10所示，U2＝f（I2）称为变压器的外特性曲线。对电阻性和电感性负载而言，电压U2 随电流I2 的增加而下降。

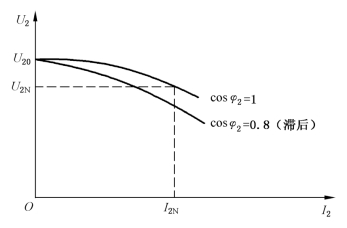
图4-10　变压器的外特性

变压器从空载到额定负载，二次绕组电压变化程度与空载电压的比值，称为电压变化率，即

在一般变压器中，由于其电阻和漏磁感抗均甚小，电压变化率是不大的，一般在5%以内。

例4-2 在图4-11中，交流信号源的电压US＝120V，内阻R0＝800Ω，负载电阻RL＝8Ω。（1）当RL 折算到原边的等效电阻R′L＝R0 时，求变压器的匝数比和信号源输出的功率；（2）当将负载直接与信号源连接时，信号源输出多大的功率？

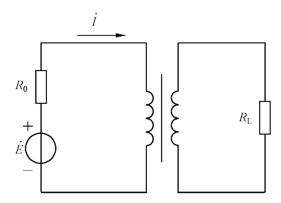
图4-11　例4-2图

解 （1）变压器的匝数比为

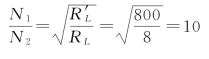
信号源的输出功率为

（2）当将负载直接接在信号源上时