若将三相负载ZA、ZB、ZC 的一端连在一起，成为一个公共点N′（称为负载的中性点），并接到三相电源的中性线上，而各负载的另一端分别接到三相电源的相线上，就构成星形联结。用四根导线将电源和负载连接起来的三相电路，称为三相四线制电路，负载星形联结的三相四线制电路一般可用如图3-6所示的电路表示。若将中性线去掉，只用三根相线连接电源和负载，则构成三相三线制电路。

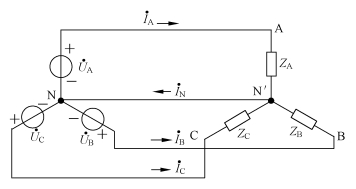
图3-6　负载星形联结的三相四线制电路

分析三相电路与分析单相电路一样，首先应在电路图上标出电压和电流的参考方向，而后应用电路的基本定律得出电压和电流之间的关系，再确定三相功率。

三相电路中流过各相负载的电流，称为相电流，用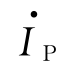表示；流经各相线的电流称为线电流，用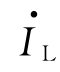表示。由图3-6可见，在负载为星形联结时，显然，相电流即为线电流，即

当各相线和中性线阻抗可忽略不计时，三相电路的计算就可归为一相计算（见图3-7，k 代表A、B、C中任一相）：

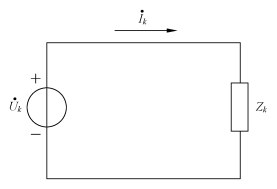
图3-7　一相电路

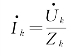
设电源相电压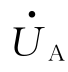为参考正弦量，则对称三相电源相电压分别为

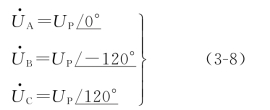
由图3-7可见，电源相电压即为每相负载电压。每相负载中的电流可分别求出，即

式中，每相负载中电流的有效值分别为

各相负载的电压与电流之间的相位差分别为

中性线中的电流可以按照图3-6中所选定的参考方向，应用基尔霍夫电流定律得出，即

若负载对称，即各相阻抗相等，即

ZA＝ZB＝ZC＝Z

亦即

|ZA|＝|ZB|＝|ZC|＝|Z|和φA＝φB＝φC＝φ

由式（3-10）和式（3-11）可见，因为三相电压对称，所以三相负载相电流也是对称的，即

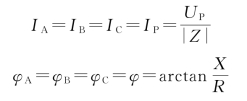
此时中性线电流等于零，即

(www.daowen.com)

电压和电流的相量图如图3-8所示。作相量图时，先画出以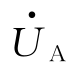为参考相量的电源相电压的相量；而后逐相按照式（3-9）画出各相电流的相量。

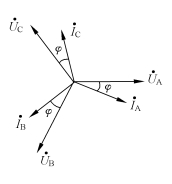
图3-8　对称负载星形联结时电压和电流的相量图

对称三相电路中性线中既然没有电流通过，则可将中性线去掉，因此如图3-6所示的电路就变为如图3-9所示的电路，这就是三相三线制电路。需要指出的是，只有对称电路可以去除中性线。

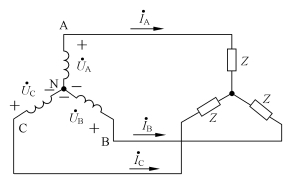
图3-9　负载星形联结无中性线

综上所述，在星形联结的对称三相电路中：

（1）由于三相电动势和负载的对称性，各相电压和电流也都是对称的。因此，只要某一相电压、电流求得，其他两相就可以根据对称关系直接写出。

（2）有中性线时，各相电流仅由各相电压和各相阻抗决定。各相的计算具有独立性。也就是说，三相对称电路的计算可以归结为一相来计算。

例3-1 有一星形联结的三相负载，每相的电阻R＝6Ω，感抗XL＝8Ω。电源电压对称，设uAB＝sin（ωt＋30°）V，试求各相电流相量。

解 因为负载对称，只需计算一相即可，现以A 相为例。

由已知uAB瞬时值表达式可写出其相量为

则相电压有效值为

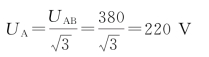
因uA 滞后于uAB30°，则

A 相电流有效值为

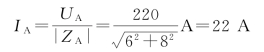
iA 滞后于uAφ 角，即

所以

因为电流对称，其他两相的电流为

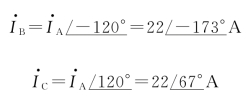
电压与电流的相量图如图3-10所示。

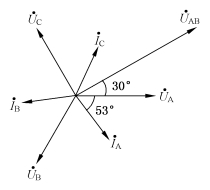
图3-10　例3-1图