图2-14a所示为电容元件的正弦交流电路，是由线性电容元件与正弦电源连接的电路。当电容器两端的电压发生变化时，电容器极板上的电荷（量）也要随着发生变化，在电路中就引起电流的变化。

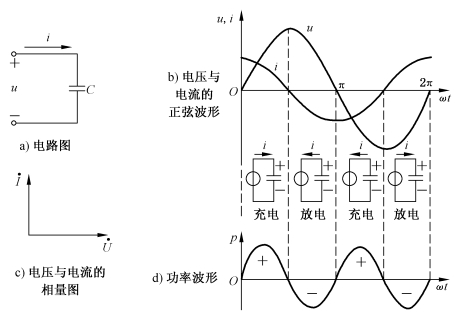
图2-14　电容元件的交流电路

设电压为参考正弦量，即

则

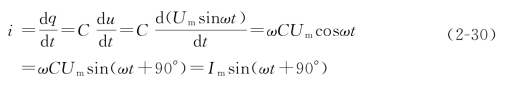
式中，Im＝ωCUm。

由式（2-29）和式（2-30）可见，电容元件交流电路中，电压的幅值（或有效值）与电流的幅值（或有效值）之比值为1/（ωC），即

与电阻元件交流电路相比较，1/（ωC）有类似于电阻R 的作用，当电压一定时，1/（ωC）越大，则电流越小。可见1/（ωC）具有阻碍交流电流通过的性质，所以称1/ωC 为容抗，用XC 表示，即

式中，若f 的单位用Hz，C 的单位用F，则XC 的单位为Ω。

电容元件的电压滞后于电流90°（相位差φ＝－90°）。表示电压u 和电流i的正弦波形如图2-14b所示。

容抗XC 与电容C、电源的频率f 成反比，因此，电容元件对高频电流所呈现的容抗很小，而对直流电流（f＝0）所呈现的容抗XC→∞，则可视作开路。因此，电容元件有通交流隔直流的作用。

如用相量表示电压与电流的关系，则为

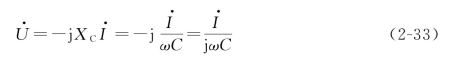
式（2-33）同时说明了电压u 和电流i 的大小关系与相位关系。电压的有效值等于电流的有效值与容抗的乘积，在相位上电压比电流滞后90°。电压和电流的相量图如图2-14c所示。

在电容元件交流电路中，瞬时功率的变化规律为

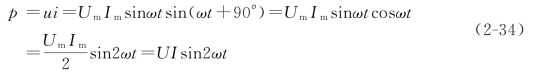
由式（2-34）可见，p 是一个幅值为UI，并以2ω 的角频率随时间变化的交变量，其变化波形如图2-14d所示。

在电压的第一个和第三个1/4周期内，电压在升高，即电容元件在充电，电容元件从电源吸收电能储存在电场中，此时瞬时功率为正；在第二个和第四个1/4周期内，电压降低，即电容元件在放电，电容元件将充电时储存的电场能量回馈给电源，所以瞬时功率为负。可见电容元件也是储能元件。(www.daowen.com)

一个周期内瞬时功率的平均值，即电容元件的有功功率为

从图2-14d的功率波形也容易看出，p 的平均值为零。这说明电容元件与电感元件一样，是一种不消耗能量的无源元件。

由上述可知，在电容元件的交流电路中，没有能量消耗，只有电源与电容元件间的能量互换。这种能量互换的规模，用无功功率Q 来衡量。

定义电容元件的无功功率等于瞬时功率的幅值，即

为体现电容与电感不同的性质，电容性无功功率取负值。

例2-7 流过C＝0.2F电容的电流为i（t）＝sin（100t－60°）A，求电容电压u（t）和电容的瞬时功率p。

解 将电流用相量形式表示为

电容电压相量为

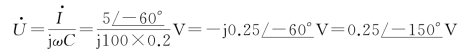
电压瞬时值形式为

瞬时功率为

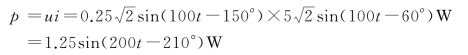
以上介绍了电阻、电感、电容元件的正弦交流电路，表征这些元件特性的唯一参数是电阻R、电感L 和电容C。而实际电路中往往同时具有这三种参数，这时可以将其视为上述元件的组合加以分析。

[思考题]

1.电感元件中通过恒定电流时可视作短路，此时电感L 是否为零？ 电容元件两端加恒定电压时可视作开路，此时电容C 是否为无穷大？

2.判断下列各式的正误。

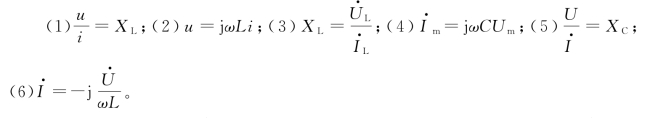
3.一个电感线圈接在U＝100V 的直流电源上，电流为20A；若接在f＝50Hz、U＝220V 的交流电源上，则电流为14.1A。求该线圈的电阻和电感。