电感元件的正弦交流电路是由非铁心线圈(线性电感元件)与正弦电源连接的电路。假定这个线圈只具有电感L,而电阻R 极小,可以忽略不计。当电感线圈中通过正弦电流i 时,其中产生自感电动势eL,其方向与电流变化的方向相反。设电流i、电动势eL 和电压u 的参考方向如图2-13a所示。

图2-13 电感元件的交流电路
设电流为参考正弦量,即
![]()
则

式中,Um=ωLIm。
由式(2-21)和式(2-22)可见,电感元件交流电路中,电压的幅值(或有效值)与电流的幅值(或有效值)之比值为ωL,即
![]()
与电阻元件交流电路相比较,ωL 有类似于电阻R 的作用,当电压一定时,ωL 越大,则电流越小。可见ωL 具有阻碍交流电流通过的性质,所以称ωL 为感抗,用XL 表示,即
![]()
式中,若f 的单位用Hz,L 的单位用H,则XL 的单位为Ω。
电感元件的电压与电流相位差φ=90°,即电压超前于电流90°。表示电压u和电流i的正弦波形如图2-13b所示。
感抗XL 与电感L、电源的频率f 成正比,因此,电感线圈对高频电流的阻碍作用很大,而对直流电流(f=0,XL=0)则可视作短路。这种特性一般叫作通直流阻交流。
必须指出,感抗只能表示电感元件电压与电流幅值(或有效值)的比,不能表示它们瞬时值的比,因为在电感元件的交流电路中,电压与电流瞬时值之间成导数的关系,而不是成正比关系。
如用相量表示电压与电流的关系,则为
![]()
式(2-25)同时说明了电压u 和电流i 的大小关系与相位关系。电压的有效值等于电流的有效值与感抗的乘积,在相位上电压超前于电流90°。电压和电流的相量图如图2-13c所示。
在电感元件交流电路中,瞬时功率的变化规律为(https://www.daowen.com)

由式(2-26)可见,p 是一个幅值为UI,并以2ω 的角频率随时间变化的交变量,其变化波形如图2-13d所示。
在电流的第一个和第三个1/4周期内,瞬时功率p 为正,即电感元件从电源吸收电能转化为磁场能量;在第二个和第四个1/4周期内,瞬时功率p 为负,元件中的磁场能量转化为电能回馈给电源。这是一种可逆的能量转换过程。在一个周期内,线圈从电源取用的能量一定等于它回馈给电源的能量。可见电感元件不消耗能量,是储能元件。
一个周期内瞬时功率的平均值,即电感元件的有功功率为
![]()
从图2-13d的功率波形也容易看出,p 的平均值为零。
从上述可知,在电感元件的交流电路中,没有能量消耗,只有电源与电感元件间的能量互换。这种能量互换的规模,用无功功率Q 来衡量。
定义电感元件的无功功率等于瞬时功率的幅值,即
![]()
无功功率并不等于单位时间内互换了多少能量。定义电感元件的无功功率为电感性无功功率,取正值。无功功率的单位是乏(var)或千乏(kvar)。
应当指出,电感元件和后面要讲的电容元件都是储能元件,它们与电源间进行能量互换是工作所需。这对电源来说也是一种负担,但对储能元件本身来说,没有消耗能量,故将往返于电源与储能元件之间的功率称为无功功率。
例2-6 L=2H 的电感两端电压为u(t)=![]() sin(100t-45°)V,求流过电感的电流及电感的瞬时功率p。
sin(100t-45°)V,求流过电感的电流及电感的瞬时功率p。
解 将电压用相量形式表示为
![]()
电感电流相量为

电流瞬时值形式为 i(t)=![]() sin(100t-135°)A
sin(100t-135°)A
瞬时功率为
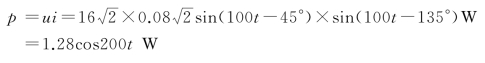
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






