如前所述，一个正弦量可以用三角函数来表示，如i（t）＝Imsin（ωt＋φ）。还可以用如图2-2所示的正弦波形来表示。这两种表示法不便于进行加、减、乘、除等运算。为了便于正弦交流电路的分析及计算，行之有效的方法是用相量表示正弦量，即相量表示法。相量表示法的基础是复数。

设复平面中有一复数A，其模为r，辐角为φ，如图2-6所示。其在横轴上的投影是复数A 的实部，a＝rcosφ，在纵轴上的投影是复数A 的虚部b＝rsinφ。若将该复数A 以ω 角速度作逆时针方向旋转，并将其每时每刻在纵坐标上的投影沿时间轴展开，如：在t＝0时，u0＝Umsinφ；在t＝t1 时，u1＝Umsin（ωt1＋φ）。则可得到如图2-7所示的正弦波形。可见，正弦量可以用复数来表示。

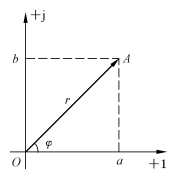
图2-6　复数的几何表示

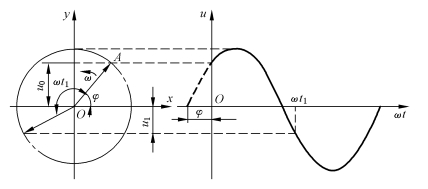
图2-7　正弦量与复数的关系示意图

根据复变函数的相关知识，复数可表示为

式中，r＝，φ＝arctan，ejφ＝cosφ＋jsinφ （欧拉公式）。

可见，复数A 决定于它的模和辐角，即复数有两个要素。在同一线性的正弦交流电路中，所有的激励和响应都是同频率的正弦量，激励的频率决定了响应的频率，因此，若认为频率是已知或默认的，则表示正弦量的三要素只有幅值（有效值）和初相位是未知量。

如果用复数表示正弦量，则复数的模即为正弦量的幅值或有效值，复数的辐角即为正弦量的初相位。为了与一般的复数相区别，将表示正弦量的复数称为相量，并在大写字母上加“·”。其中有向线段长度等于正弦量幅值的相量称为幅值相量，用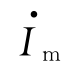或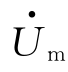表示；长度等于有效值的相量称为有效值相量，用 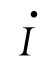或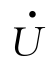表示。同样，表示正弦量的相量也有4种形式，即代数式、三角式、指数式和极坐标式。

电压与电流的幅值相量可表示为

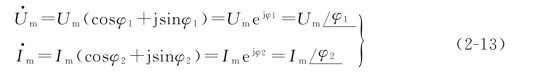
有效值相量可表示为

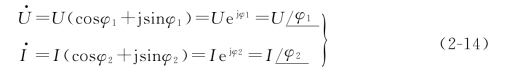
本书中除非特别说明，相量都采用有效值相量的形式表示。注意，相量只是表示正弦量，而不是等于正弦量。

按照各个正弦量的大小和相位关系，用初始位置的有向线段画出的若干个相量的图形，称为相量图。在相量图上能形象地看出各个正弦量的大小和相互间的相位关系。例如，在图2-3中用正弦波形表示的电压u（t）和电流i（t）两个正弦量，如用相量图表示则如图2-8所示，电压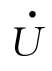相量 比电流相量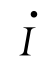 超前φ 角，也就是正弦电压u（t）比正弦电流i（t）超前φ 角。

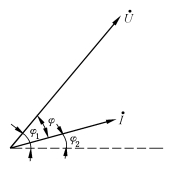
图2-8　相量图

只有正弦量才能用相量表示，相量不能表示非正弦周期量。只有同频率的正弦量才能画在同一相量图上，不同频率的正弦量不能画在一个相量图上，否则无法比较和计算。

由上可知，表示正弦量的相量有两种形式：相量图和相量式（复数式）。两个或多个正弦量的加减运算可用相量的代数式，乘除运算可用相量的指数式或极坐标式来进行。

在图2-9中，如以ejα（α＞0）乘相量＝rejφ，则得

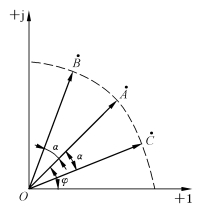
图2-9　相量的超前与滞后

即相量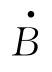 的大小仍为r，但与实轴正方向间的夹角为φ＋α。可见一个相量乘上ejα后，即向前（逆时针方向）转了α 角，就是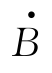相量 比相量 超前了α 角。

同理如以e－jα乘相量，则得

即向后（顺时针方向）转了α 角，就是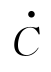相量 比相量滞后了α 角。(www.daowen.com)

当α＝±90°时，有

e±j90°＝cos90°±jsin90°＝±j

因此任意一个相量乘上＋j后，即向前旋转了90°；乘上－j后，即向后旋转了90°。所以j称为旋转90°的算子。

例2-2 已知i1（t）＝5sin（314t＋60°）A，i2（t）＝－10cos（314t＋30°）A，试写出代表这两个正弦电流的幅值相量，并作相量图。

解

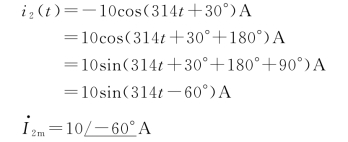
其相量图如图2-10所示。

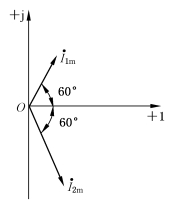
图2-10　例2-2图

以余弦函数表示的正弦量都要将其化为正弦函数表达式，再写出相量。

例2-3 写出表示uA＝，uC＝ 的相量，并作相量图。

解

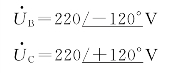
其相量图如图2-11所示。

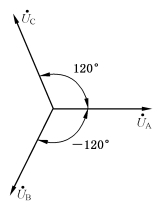
图2-11　例2-3图

例2-4 已知i1＝20sin（ωt＋60°）A，i2＝10sin（ωt－45°）A，求电流i＝i1＋i2。

解 用相量表示法，将i1、i2 写成幅值相量形式，即

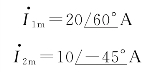
求得电流i的幅值相量为：

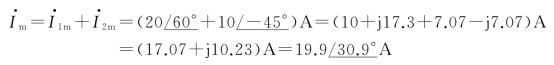
则电流i的瞬时值表达式为

i＝Imsin(ωt＋φ)＝19.9sin(ωt＋30.9°)A

采用相量来表示正弦量，使得相应的运算变得简单易行，从而使正弦交流电路的分析得到简化，另外，相量图也是分析正弦量的常用方法。需要指出的是，相量法的实质是将同频的正弦量用复数形式表示，因此相量法只是一种分析交流电路的数学工具。

[思考题]

1.不同频率的几个正弦量能否用相量表示在同一相量图上？ 为什么？

2.已知u1＝sinωtV，u2＝sin（ωt＋90°）V，u3＝sin（ωt－90°）V，u＝u1＋u2＋u3。试用相量式和相量图求u。

3.判断下列各式的正误。

(1)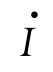＝10e45°；(2)u＝20(cos30°＋jsin30°)；(3)i＝sin(ωt＋60°)＝3ej60°A；(4)U＝50ej30°＝50sin(ωt＋30°)V；(5)I＝。