正弦量是随时间而变化的，要确定一个正弦量还须从计时起点（t＝0）上看。所取的计时起点不同正弦量的初始值（t＝0时的值）就不同，到达幅值或某一特定位所需的时间也就不同。

式（2-1）中的ωt＋φ 称为正弦量的相位角或相位。当相位角随时间连续变化时，正弦量的瞬时值随之连续变化。t＝0时正弦量的相位角，称为初相位角或初相位。初相位有正负之分，习惯上常取初相位绝对值小于180°。

两个同频率正弦量的相位角之差称为相位差，用φ 表示。在同一正弦交流电路中，电压u（t）和电流i（t）的频率是相同的，但初相位不一定相同。如图2-3所示，图中u（t）和i（t）的波形可用下式表示

图2-3　u 与i的相位关系

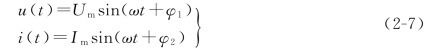
它们的频率相同，初相位分别为φ1 和φ2。u（t）和i（t）的相位差为

可见，两个相同频率正弦量的相位差就是它们的初相位之差。虽然两个同频率正弦量的相位角都随时间改变，但它们的相位差却保持不变，即与时间t无关。

由图2-3的波形可见，因为u（t）和i（t）的初相位不同（不同相），所以它们的变化步调是不一致的，即不同时到达正的幅值或零值。图中，φ1＞φ2，所以u（t）比i（t）先到达正的幅值，称作u（t）的相位超前于i（t）的相位一个φ 角，或i（t）的相位滞后于u（t）的相位一个φ 角。

如图2-4a所示，如果两个同频率正弦量的初相位相同，则称它们是同相。图2-4b所示两正弦量相位差等于180°，称为反相。图2-4c所示两正弦量相位差等于90°，称为正交。

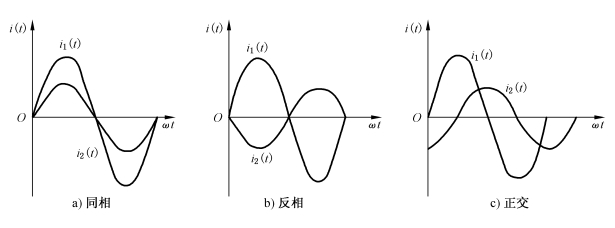
图2-4　同频率正弦量的相位关系

初相位为零的正弦量称为参考正弦量，在分析和计算交流电路时，为了简化计算，常常先选定某一个正弦量为参考正弦量，然后再求出其他正弦量与参考正弦量之间的相位关系。

对于不同频率的正弦量，不能应用相位差的概念，因为它们相位角的差是随时间而变化的。

例2-1 用示波器测得图2-5a电路的各电压如图2-5b所示。（1）写出uab、ucb的表达式；（2）求uab与ubc的相位差。

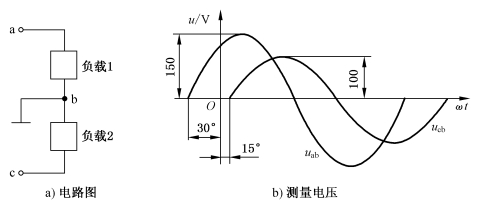
图2-5　例2-1图(www.daowen.com)

解 （1）uab＝150sin（ωt＋30°）V

ucb＝100sin(ωt－15°)V

(2)ubc＝－ucb＝－100sin(ωt－15°)V＝100sin(ωt＋165°)V

φ＝φ1－φ2＝30°－165°＝－135°

计算表明，uab滞后于ubc135°。

综上所述，正弦量的基本特征表现为它的变化快慢、变化幅度以及初始情况三个方面，用频率、幅值和初相位这三个量来描述。这三个量称为正弦量的三要素，其中频率和幅值与计时起点的选择无关，初相位则与计时起点的选择有关。知道了三要素，一个正弦量就完全被确定了。

[思考题]

1.若某电路中，u＝380sin（314t－45°）V：

（1）试指出它的频率、周期、角频率、幅值、有效值及初相位各为多少？

（2）画出其波形图。

2.正弦量的幅值和有效值是否随时间变化？ 它们的大小与频率、相位有没

有关系？

3.计算下列两正弦量的相位差：

(1)u1(t)＝；

(2)i1(t)＝15sin(100πt＋30°)，i2(t)＝10sin(200πt＋60°)；

(3)u1(t)＝10sin(100πt＋120°)，i2(t)＝－10cos(100πt－30°)。

4.5A 的直流电流和最大值为6A 的正弦交流电流，分别流过阻值相同的电阻，试问：在相同的时间内，它们谁发热量较多？ 为什么？