任何一个线性有源二端网络都可以用一个理想电压源US 和内阻R0 串联的电源来等效代替(见图1-45)。等效电源中的电压源电压US 就是有源二端网络的开路电压UOC,即将负载断开后a、b两端之间的电压。等效电源的内阻R0 等于有源二端网络中所有电源均不作用(将各个理想电压源短路,即其电压为零;将各个理想电流源开路,即其电流为零)所得到的无源网络a、b两端之间的等效电阻。这就是戴维南定理。
图1-45所示的等效电路是一个最简单的电路。其中,电流可由下式计算

图1-45 戴维南等效电路
![]()
等效电源的电压和内阻可通过实验或计算得出。
例1-15 电路如图1-46所示,试用戴维南定理求:(1)电流I;(2)3Ω 电阻所消耗的功率P3Ω。
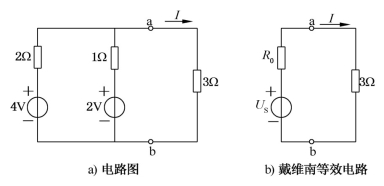
图1-46 例1-15图
解 在如图1-46a所示电路中,将电流I 所在支路与原电路在节点a、b处断开,而从a、b节点向左看的网络即为一有源二端网络,可等效为图1-46b所示的戴维南等效电路。欲求电流I,只要求出等效电源的电压US(即开路电压UOC)和戴维南等效电阻R0 即可。
(1)求等效电源的电压US,即开路电压UOC。其等效电路如图1-47所示,可解得电流

图1-47 求UOC的电路
![]()
由KVL得
UOC=(1×I1)V+2V=(1×0.67+2)V=2.67V
US=UOC=2.67V
(2)求戴维南等效电阻R0。其等效电路如图1-48所示,则

图1-48 求R0 的电路
![]()
(3)在图1-46b中,求得电流I 为
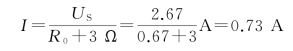
3Ω 电阻所消耗的功率为
P3Ω=3Ω×I2=3×(0.73)2W=1.6 W
例1-16 电路如图1-49a所示,已知US1=8V,US2=5V,IS=3A,R1=2Ω,R2=5Ω,R3=2Ω,R4=8Ω,试用戴维南定理求通过R4 的电流I4。(https://www.daowen.com)
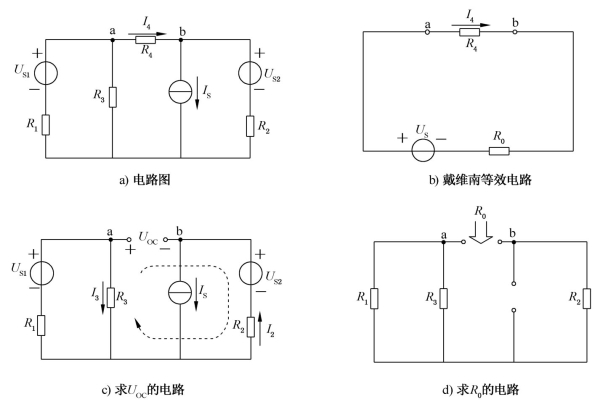
图1-49 例1-16图
解 从节点a、b处断开,将待求支路提出,可将图1-49a的电路等效为图1-49b所示的戴维南等效电路。
(1)求等效电源的电压US,即二端网络的开路电压UOC,在图1-49c中,由于

选图中虚线所示回路,由KVL得
UOC+US2-R2I2-R3I3=0
UOC=-US2+R2I2+R3I3=(-5+5×3+2×2)V=14V
US=UOC=14V
(2)求等效电源内阻R0,在图1-49d中

(3)在图1-49b中,可求得
![]()
例1-17 电路如图1-50所示,试用戴维南定理求R=2.5kΩ电阻中的电流I。
解 图1-50a的电路可等同于图1-50b的电路。

图1-50 例1-17图
(1)将a、b间开路,求等效电源的电压US,即开路电压UOC

(2)令所有电压源不作用,求等效电源的内阻R0
R0=3kΩ∥6kΩ+2kΩ∥1kΩ∥2kΩ=2.5kΩ
式中,“∥”表示电阻并联。
(3)戴维南等效电路如图1-51所示,则电阻R 中的电流为

图1-51 例1-17等效电路
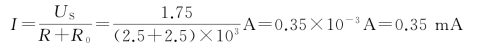
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






