基尔霍夫电流定律用来确定连接在同一节点上的各支路电流之间的关系。由于电流的连续性，电路中任何一点（包括节点在内）均不能堆积电荷，因此，在任一瞬时，流入电路中任一节点的各支路电流之和等于从该节点流出的各支路电流之和。基尔霍夫电流定律是电流连续性原理的反映。

例如，图1-23电路中，对于节点a，在图示的各支路电流参考方向下，可写出

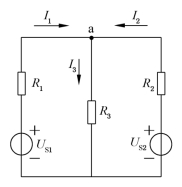
图1-23　基尔霍夫电流定律电路图

式（1-26）是基尔霍夫电流定律的数学表达式，称为节点电流方程。如把流入节点的支路电流取正号，流出节点的支路电流取负号，则上式可改写为可见，在任一瞬时，与任一节点关联的支路电流的代数和等于零。由此可见，基尔霍夫电流定律与各支路中元件无关。

例1-2 在图1-24中，I1＝5A，I2＝－3A，I3＝1A，试求支路电流I4 的大小。

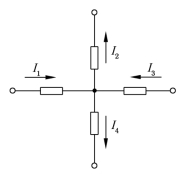
图1-24　例1-2图

解 根据图中所标示的各支路电流的参考方向，由基尔霍夫电流定律可列出

I1－I2＋I3－I4＝0

5A－(－3)A＋1A－I4＝0

解得(www.daowen.com)

I4＝9A

此计算结果说明，有些支路的电流可能是负值，这是由于所选定的电流的参考方向与实际方向相反所致。由本例可见，I 前的正负号是由基尔霍夫电流定律根据电流的参考方向确定的，括号内数字前的正负号则是表示电流本身数值的正负。

基尔霍夫电流定律通常应用于节点，也可以将其推广应用于包围部分电路的任一假设的闭合面（称为广义节点）。例如，图1-25所示的闭合面包围的是一个三角形电路，有3个节点。应用KCL可列出

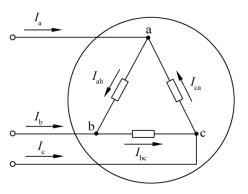
图1-25　基尔霍夫电流定律的推广应用

Ia＝Iab－Ica

Ib＝Ibc－Iab

Ic＝Ica－Ibc

上列三式相加，便得

Ia＋Ib＋Ic＝0

或

∑I＝0

可见，在任一瞬时，通过任一广义节点的电流的代数和也恒等于零。