为了说明数字滤波的作用，下面引入一个实例：

设有一个模拟信号i（t），其含有直流分量、基波和四次谐波，数学表达式为

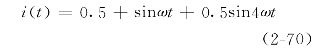
其波形如图2-20所示。

对于该信号每隔30°采样一次，即采样间隔为，从t=0到t=20ms共采样13点，这些采样点的数值列在表2-4中。

若给出的数字滤波器如图2-21所示，利用同样的方法对h（t）按每隔进行采样，则得到的采样值如表2-5所示。

表2-4　采样值数据表

表2-5　给定滤波器的采样值

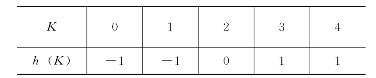
整个滤波的过程就是用数字滤波器h（K）的值与输入信号i（K）的对应值相乘后再求和，即可得到滤波后的输出。

假定输出信号为y（n），那么

n=0时，即

y（0）=h（0）i（0）+h（1）i（—1）—h（2）i（—2）

+h（3）i（—3）+h（4）i（—4）

因为h（4）以后的值均为零，故（2-71）式中的N取4。(www.daowen.com)

在计算y（0）时，需用到i（—1），i（—2），i（—3）及i（—4）。这些值在表2-4中没有表示。如果以t=0时发生短路，则t＜0为正常负荷状态，所以从y（0）到y（3）的数据有一部分是故障前，有一部分是故障后，这就相当于模拟滤波器的过渡过程。

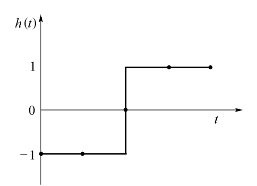
图2-21　滤波器图形

滤波器的第一个有意义输出是y（4）

y（4）=h（0）i（4）+h（1）i（3）+h（2）i（2）

+h（3）i（1）+h（4）i（0）

根据表（2-4）的数据，求出y（n）的值列于表2-6中。

将这些点画在图2-22中，可见连接这些点的波形是正弦基波。但其各点的值比输入的基波值扩大了2.732倍。如果将各点值均除以2.732，则输出信号刚好是输入信号中基波分量的采样值。而i（t）中的直流分量及四次谐波分量均被滤掉。

表2-6　输出数值表

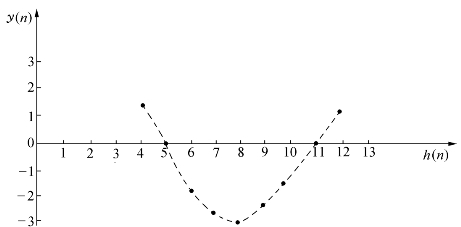
图2-22　滤波器输出波形图

从这个例子可以看出：

（1）数字滤波的过程事实上是用一个已知函数h（n），对h（t）进行采样得到的离散时域函数与经过采样的输入信号x（n）时行卷积的过程。式（2-71）即为离散时域卷积公式。

（2）数字滤波器也存在过渡过程，即滤波器的稳态输出需经过一定延时。延时的长短与所选的已知函数h（n）的数据窗有关。

（3）数字滤波器的滤波效果可以从分析h（t）的幅频特性得到。