图2-13　半周积分算法

半周积分和导数算法是用来处理纯正弦量的理想采样值。而在实际应用中，对于故障后的电流和电压中都含有各种暂态分量，而且数据采集系统还会引入各种误差，所以这一类算法要获得精确的结果，需要与数字滤波器配合使用。

1.半周积分算法

半周积分算法的实质是根据一个正弦信号在任意半个周期内绝对值的积分正比于其幅值。如图2-13所示。现以正弦电压信号为例来进行说明。若正弦电压的表达式为

u=Umsin（ωt+φ）

则其绝对值在半周期内的积分

在微机保护中，求此积分的方法有两种。第一种方法是用梯形法则近似求出。

式中　uk——第k次采样值；

N——每工频周期采样点数。

求出积分值M后，可求出电压的有效值

按式（2-47）求出的有效值会产生误差，产生误差的原因有两个：其一是由于用梯形法则求面积是一种近似算法，这种误差将随采样频率的提高而减少。今有一个正弦信号，其有效值为U=220V。按N=12，若使第一个采样点的初相角为0°，则由式（2-12）求出的M值为　1368.4×10—3，于是求出电压的有效值U为

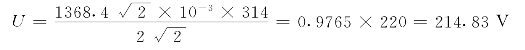
相对误差为

而当N=20时，第一个采样点初相角仍为0°，则

其二是在同样的采样频率下，按式（2-46）计算出的M值与第一个采样点的初相角有关。

仍假设U=220V，N=12，第一个采样点的初相角分别为0°，5°，10°，15°时，计算出的有效值分别为214.83V，219.032V，221.54V，222.42V，则相对误差分别为2.35%，0.44%，0.7%，1.1%。

第二种方法是用采样值求和代替积分值。该积分值与信号的幅值成比例。因而有

从而可求出电压的有效值U。

在式（2-48）、（2-49）中，系数K随第一个采样点的初相角变化。确定系数K的方法是：按第一个采样点的初相角为0°求出M值，K取为此时M与Um的比值。按采样频率为600，N=12，则K=3.732。该方法的计算结果也会产生误差。其误差随第一个采样点的初相角变化。当第一个采样点的初相角为0°，5°，10°，15°时，其相对误差分别为0，1.96%，3.1%，3.53%。同时提高采样频率也可以减少误差。

因为正弦波的周期为20ms，故半周积分算法需要的数据窗为10ms。半周积分算法的优缺点是：

（1）数据窗比较长。

（2）半周积分算法具有一定的滤除高频分量的作用。因为在积分的过程中，谐波分量的正、负半周相互抵消。

（3）该算法不能滤除直流分量。

（4）该算法运算分量小，在一些对精度要求不高的电流、电压保护中，可以采用此种算法。必要时可用差分滤波器来抑制信号的直流分量。

2.导数算法

(www.daowen.com)

图2-14　用差分近似求导的图形

在第一节中曾经说明：导数算法是利用正弦函数的导数位余弦函数的特点计算正弦电压、电流的幅值。这种算法只需要知道输入正弦量在某一时刻t1的采样值及该时刻采样值的导数即可求出有效值。意即

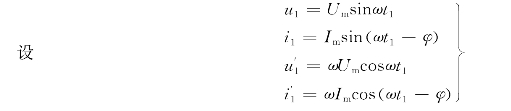
则

为求导数，可取t1时刻为两个相邻采样时刻tk和tk+1的中点，正如图2-14所示。然后用差分来近似求取导数值。

在计算机中，求取u1、i1、的方法分别为

式（2-51）说明：

（1）t1时刻的值是取tk和tk+1时刻的采样值的平均值；

（2）t1时刻的电压、电流导数值由差分求得。

对于正弦信号说来，用其平均值代替t1时刻的采样值及用差分代替求导数都会引起计算误差，此误差将随采样频率增加而减小。下面我们来分析用差分来代替求导所产生的误差。

则用差分来代替求导其导数值为

如此其相对误差为

当每周采样点数N=12时，=1.67ms，γ%=1.1%；

当每周采样点数N=20时，h=1ms，γ%=0.4%。

用相邻的两个采样值的平均值代替t1时刻的瞬时值，其所引起的误差为

这是因为在t1时刻的瞬时值为

u1=Umsinωt1

令φ=ωh，tk，tk+1时刻电压的采样值在理论上

于是有

可见，t1时刻的平均值与t1时刻的瞬时值两者相差一个误差因子。

表2-1　用差分代替求导数和用平均值代替瞬时值的相对误差表

可见用差分代替求导数和用平均值代替瞬时值所产生的误差均与φ有关，即与采样频率有关。

表2-1列出了当采样频率从300～2400Hz时，用差分代替求导数和用平均值代替瞬时值产生的相对误差。

此算法的优点是占用数据窗短，只需两个采样点。但在具体应用时应注意这两个采样点应是数字滤波后的点。