1.微分算法

假定电流是纯正弦的，即

i=Imsinωt

该正弦量的一阶导数为

i′=ωImcosωt

如此，正弦量的幅值，可依下式求出

该幅值与采样的位置无关。其相角为

由式（2-35）和式（2-36）计算正弦电流的方法称为微分法。

2.差分算法

如图2-10所示，假定采样的时间间隔为h，再假定现在的采样为第k次采样，k—1，k—2，…，为第k次以前的采样，而k+1，k+2，…，为第k次以后的采样。

图2-10　差分算法采样图形

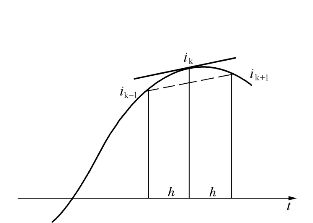
图2-11　差分算法的几何意义图形

在每一个采样瞬间其所采集的电流值分别为ik—2，ik—1，ik，ik+1，ik+2，…所谓差分算法就是利用差分来代替导数，即电流的一次差分为

电流的二次差分为

电流的一次差分也可采用下述公式计算

(www.daowen.com)

该算式的几何意义示于图2-11中，即用弦的斜率代替切线的斜率。

将式（2-39）代入式（2-35）和式（2-36）中，便可计算出电流的幅值和相位。

3.二阶导数算法

该种算法采用的是电流的一阶和二阶导数，这种算法是西屋公司提出的，称为Prodar算法，算法的步骤是：

（1）若　i=Imsinωt

i′=ωImcosωt=ωImsin（ωt+90°）

i″=—ω2Imsinωt=ω2Imcos（ωt+90°）

在计算时，一阶和二阶导数用一阶和二阶差分来代替，根据式（2-39）和式（2-38）有

图2-12　同步采样算法图形

采用二阶导数计算可以减少直流暂态分量和低频信号的影响。上述方法常称为不同步算法，即其采样过程不需与被检测的正弦量同步，如此，在硬件电路中可以省去同步电路。

4.同步算法

所谓同步算法即是在正弦波的一个周期中，每隔一定角度采样一次，常用的有30°采样，即每个周期采样12次；还有90°采样，即每周期采样4次。为了说明简单，以90°采样为例。如图2-12所示，今设正弦电压为

u=Umsin（ωt+φ）

从图2-12可见，第k次采样和第k+1次采样的时间间隔为90°，如此，第k次采样和第k+1次采样的电压为

uk=Umsin（ωt+φ）

uk+1=Umcos（ωt+φ）

于是

采用同步算法需要在采样过程中与被测量的工频同步。