双端电源系统如图8-1所示,其中 与
与 分别表示线路两端的系统电源,两电源的模相等但存在一定相位差δ,
分别表示线路两端的系统电源,两电源的模相等但存在一定相位差δ,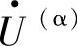 为发送端,
为发送端,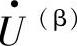 为接受端。两个电源端的母线出口处均安装有距离继电器,即K1和K2。每个继电器的下游位置都安装有经济型故障限流器(FCL),其限流阻抗均为ZFCL,忽略电阻效应,其等效分析模型如图8-2所示。图8-1中A、B两点之间为输电线路,当线路上某点经过渡电阻Rf发生接地故障时,线路的阻抗可分为Z(α)和Z(β)两部分,故障点电压用
为接受端。两个电源端的母线出口处均安装有距离继电器,即K1和K2。每个继电器的下游位置都安装有经济型故障限流器(FCL),其限流阻抗均为ZFCL,忽略电阻效应,其等效分析模型如图8-2所示。图8-1中A、B两点之间为输电线路,当线路上某点经过渡电阻Rf发生接地故障时,线路的阻抗可分为Z(α)和Z(β)两部分,故障点电压用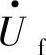 表示。
表示。
图8-1 双端电源系统接地故障分析模型
当线路发生接地短路故障时,设发送端侧线路电流为 ,接受端侧线路电流为
,接受端侧线路电流为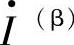 ,则流过故障过渡电阻Rf的电流为
,则流过故障过渡电阻Rf的电流为 与
与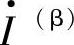 之和,即
之和,即
整理以上三式,可得
由式(8-4)可得
式中,Δ表示一算子,见式(8-6)所示:
将式(8-5)代入式(8-1)中,可得
同理,将式(8-5)代入式(8-2),可得
将式(8-8)除以式(8-7),可得到接受端电流相量与发送端电流相量之比:
电网正常运行状态下,并网的双端电源系统之间的相位差δ一般不大;当线路发生接地短路时,短时间内δ也不会发生突变。因此,在推导故障量的一般关系时,可先忽略相位差δ的影响,即认为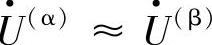 ,则接受端与发送端故障电流相量的模之比可写为
,则接受端与发送端故障电流相量的模之比可写为
当线路发生短路故障时,相对于电抗效应,输电线路上的电阻效应可忽略,即Z(α)≈jX(α),Z(β)≈jX(β),其中X(α)和X(β)分别为发送端和接受端至短路故障点的线路电抗。
由此,式(8-10)可改写成
式中,k为实数,表示接受端与发送端故障电流相量的模之比。
当忽略FCL和输电线路的电阻效应时,则发送端和接受端系统电源发出的有功功率P(α)和P(β)主要由故障过渡电阻Rf消耗,且满足
设P为发送端和接受端电源发出的总有功功率,则有以下两式:
P=P(α)+P(β)=(1+k)P(α) (8-13)
P=(I(α)+I(β))2Rf=(1+k)2I(α)2Rf (8-14)
综合式(8-13)和式(8-14)得到
若把图8-1中双端电源系统的故障过渡电阻Rf分解为两个不同电阻R(α)和R(β)的并联,则该系统就可分解为两个相对独立的单端电源故障系统的组合,如图8-2所示。在这两个新的单端系统中,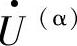 发出的有功功率P(α)只由R(α)消耗,而
发出的有功功率P(α)只由R(α)消耗,而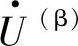 发出的有功功率P(β)只由R(β)消耗。这样,若对继电器K1进行补偿,则只需分析左侧的单电源系统;同理,对继电器K2进行补偿,则只需分析右侧的单电源系统。设两个等效单端故障系统的故障点分别为f1和f2,则f1和f2处的故障电压均为
发出的有功功率P(β)只由R(β)消耗。这样,若对继电器K1进行补偿,则只需分析左侧的单电源系统;同理,对继电器K2进行补偿,则只需分析右侧的单电源系统。设两个等效单端故障系统的故障点分别为f1和f2,则f1和f2处的故障电压均为 ,这是约束条件。(https://www.daowen.com)
,这是约束条件。(https://www.daowen.com)
图8-2 分解后的双端电源系统接地故障分析模型
由图8-2可知,R(α)和R(β)必须满足以下两式:
解式(8-16)、式(8-17),并代入式(8-11)可得
将式(8-15)代入式(8-18),可得
图8-3 等效单端系统的单相接地故障复合序网
对图8-2左边的单端等效系统应用对称分量法,可得到故障点电压和故障电流的序分量及复合序网,如图8-3所示。接受端侧系统的复合序网可同理获得。
在图8-3中,Z1(α)、Z2(α)和Z0(α)分别表示该系统复合序网的正序、负序和零序阻抗;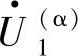 、
、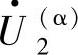 和
和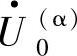 与
与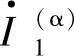 、
、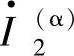 和
和 分别表示该复合序网故障点电压和电流的正序、负序和零序分量。
分别表示该复合序网故障点电压和电流的正序、负序和零序分量。
该复合序网的边界条件可写成以下三式:
由复合序网可以得到
代入式(8-22)和式(8-23),且认为Z1(α)=Z2(α),得
继续整理,即得
若将式(8-26)等号右边的式子定义为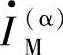 ,则有
,则有
且在式(8-27)中,定义
式中,m即为零序电流补偿系数,它表示线路中零序阻抗与正序阻抗的固有关系,取决于线路的结构。根据式(8-28),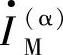 是可以通过测量单端故障电流获得的中间量。
是可以通过测量单端故障电流获得的中间量。
将式(8-27)代入式(8-26),整理得
将式(8-20)代入式(8-29),并将故障限流器(FCL)的等效限流阻抗换为jωL,得到
同理,可得系统发生三相接地短路时,补偿后继电器K1的测量阻抗Z1(α)为
根据式(8-30)和式(8-31),测量阻抗的补偿公式中已经涵盖了FCL限流电抗的影响,且其计算值在理论上不受故障过渡电阻大小的影响。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






