近区故障是考核断路器开断性能的严重故障类型。分析模型如图7-5所示，其中，L₁和C₁为线路侧的电感与对地电容。若单位长度线路电感与对地电容分别为l₁与c₁，则距离断路器s处发生短路时，L₁=l₁s，C₁=c₁s，短路电流I_ss可表示为

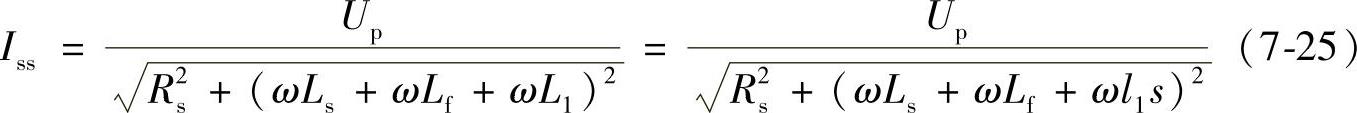
断路器断口的电弧电流过零熄灭时，u_A、uFCL和uC正好到达电压峰值U_Am、UFm和U_Cm。

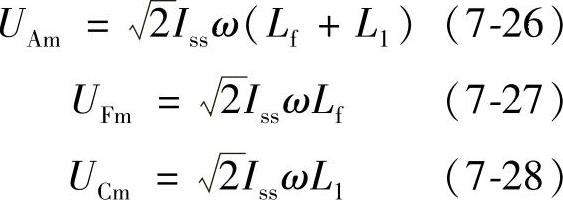
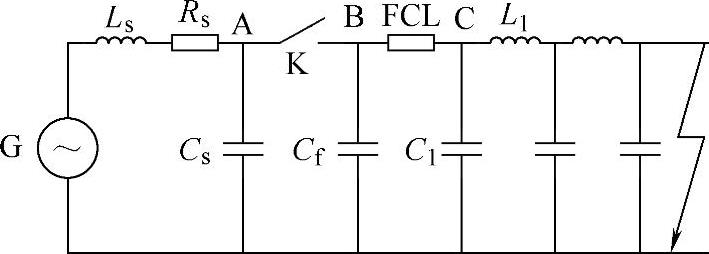
图7-5 近区故障等效电路

当断口电弧电流熄灭后，在FCL侧将主要出现两个电压振荡。首先，由于故障线路侧具有分布参数特性，造成端点C的对地电压是一个锯齿波的行波过程，其周期T₃为行波经过故障线段长度所需时间的4倍。忽略线路损耗，则行波的传播速度为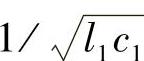，锯齿波的振荡周期为

FCL出口处C点的电压初始值为U_Cm，经T₃/2时间后将降到-U_Cm。由此可得到u_C在初始1/2周期内的电压下降率为

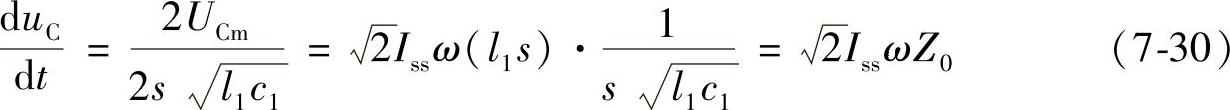
式中，Z₀是波阻抗。在初始1/2周期内，u_C的电压变化方程式为

其次，限流电抗上的电压u_FCL从U_Fm开始，也会经历一个振荡过程。由于FCL的限流电抗L_f较大，且其对地电容C_f较小（C_f<C_p和C_f<C₁），则限流电抗的电压振荡周期主要由L_f和C_p决定，仍符合式 （7-13）。

根据上述分析，可以得到近区故障时断路器的恢复电压为

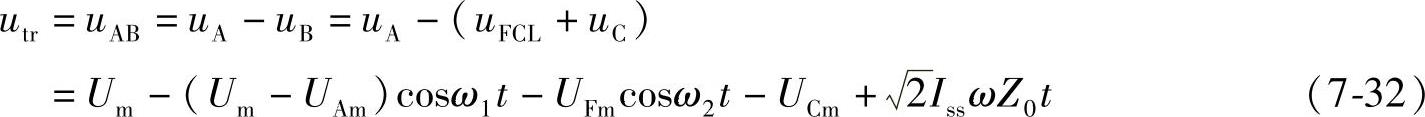
则由式（7-11），同理可计算RRRV。

t_p=T₀/2=min（T₁，T₂，T₃）/2 （7-33）式中，T₁为电源侧电容电压振荡周期；T₂为FCL限流电抗的电压振荡周期；T₃为故障线路的行波电压振荡周期。

通常，T₁>>T₃。当近区故障发生距离较小时，满足T₂>T₃，令

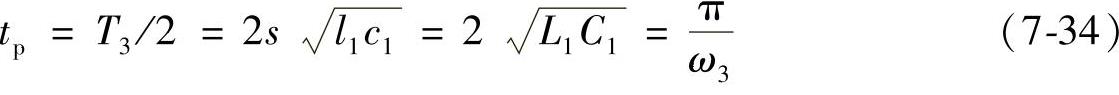
则断路器恢复电压的第一个峰值为

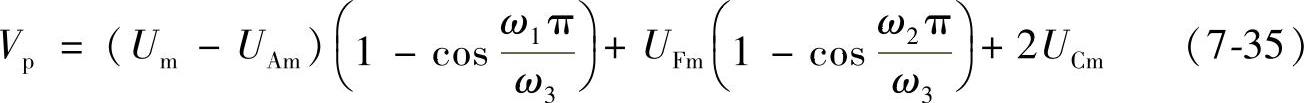
根据式（7-11）、式（7-34）和式（7-35），可得到安装经济型FCL的输电线路在skm处发生近区故障时，断路器恢复电压上升率为

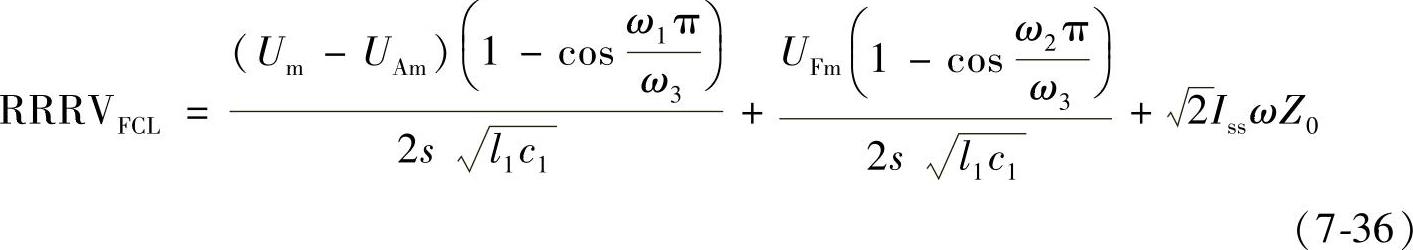
将式（7-16）代入式（7-36），得到(www.daowen.com)

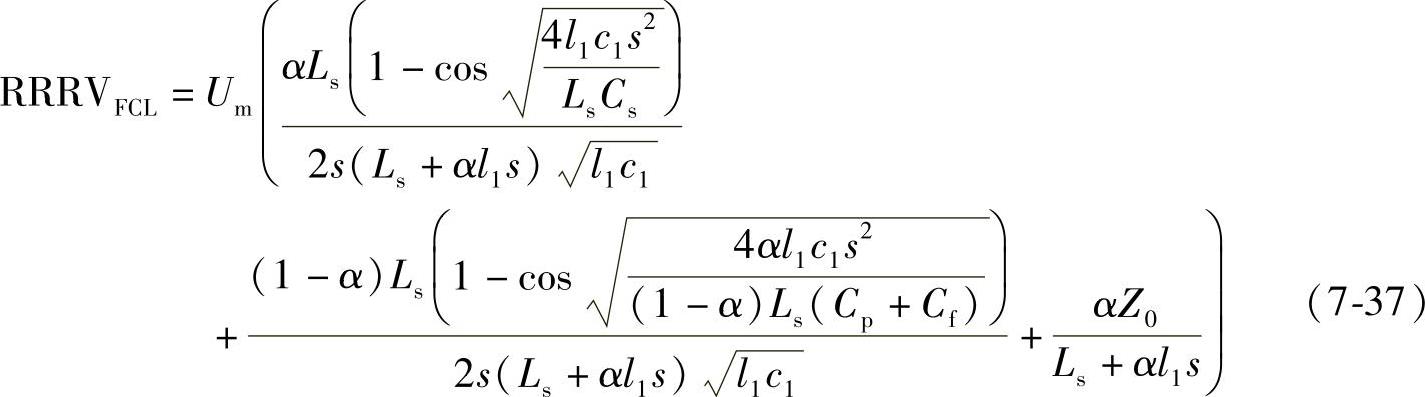
随着近区故障发生距离s的增大，T₃将增大。若满足T₃>T₂，此时将故障线段的行波电压变化近似为正弦变化，并根据

t_p=T₀/2=min（T₁，T₂，T₃）/2=T₂/2 （7-38）得到

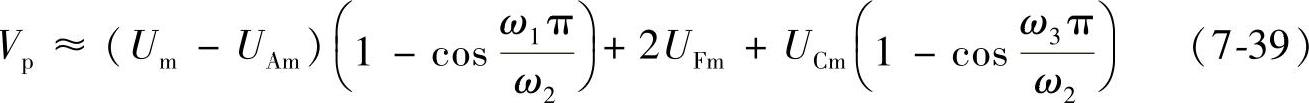
根据式（7-16）、式（7-38）和式（7-39），可得到安装经济型FCL的输电线路在skm处发生近区故障时，断路器恢复电压上升率为

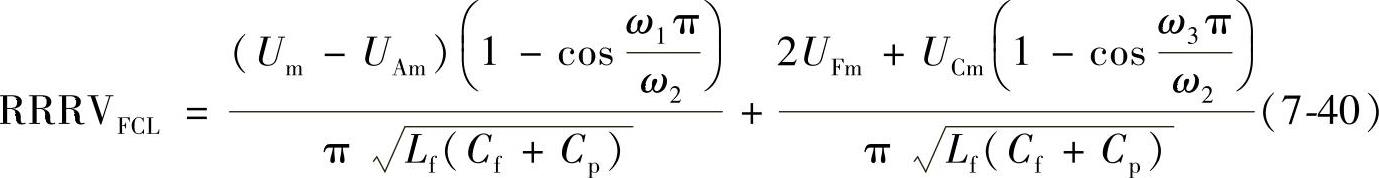
将式（7-16）代入式（7-40），得到

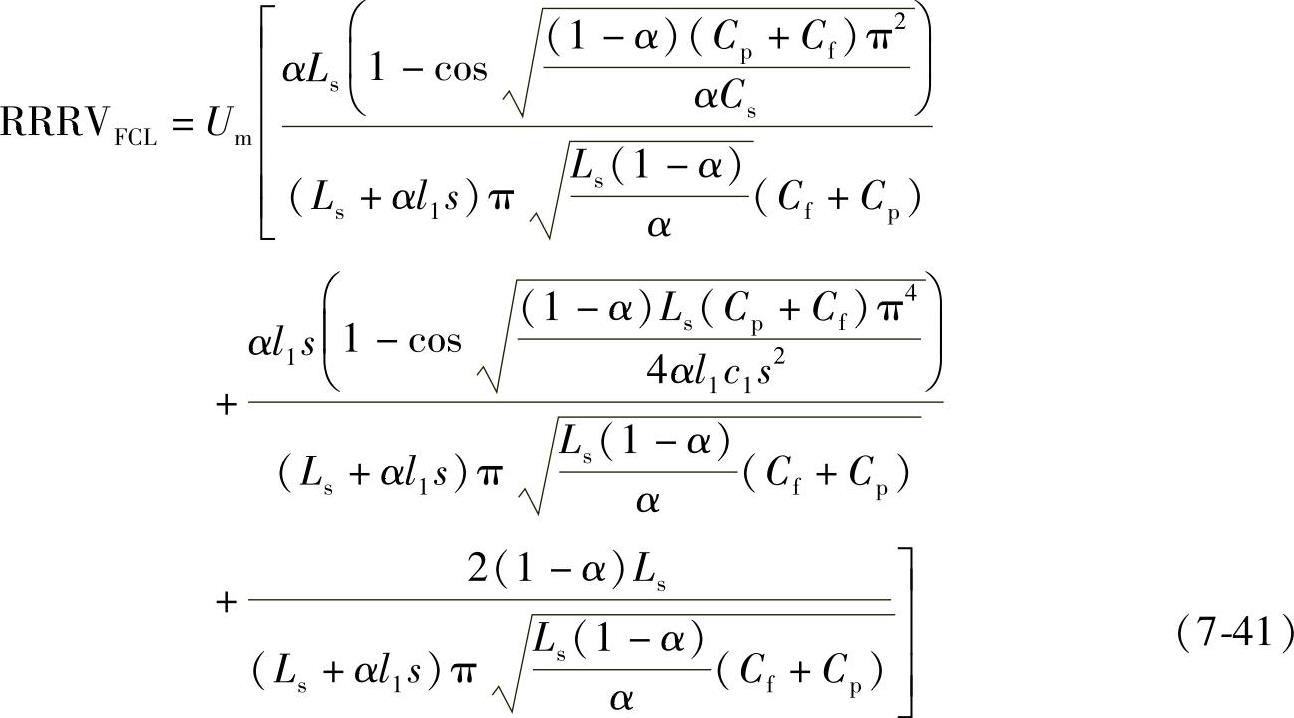
若系统中未安装FCL，即限流比为1，则系统发生近区故障时，断路器恢复电压的第一个峰值为

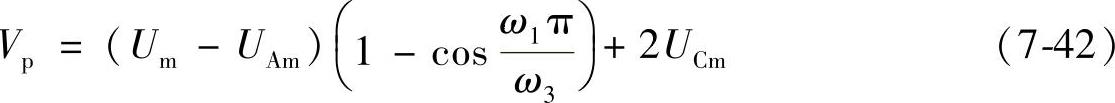
恢复电压到达第一个峰值的时间为

由式（7-16）、式（7-42）和式（7-43），可得

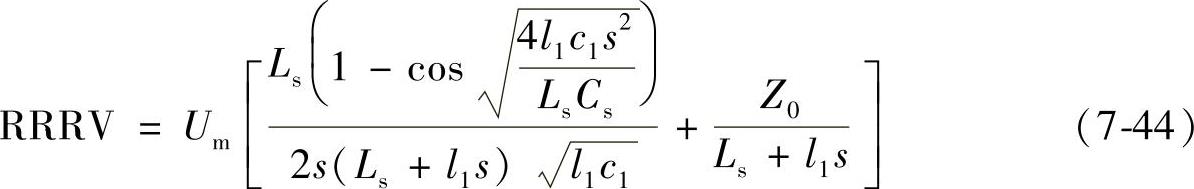
下面针对220kV系统在近区线路发生三相短路的情况进行计算分析。参数取为：U_m=180kV，L_s=10mH，R_s=0.1Ω，C_f=1nF，C_p=50nF，l₁=0.8mH/km，c₁=15nF/km，s=1km、4km、8km。分别考虑C_s=1.5μF和C_s=0.05μF两种情况，使用式（7-37）、式（7-41）和式（7-44）得到恢复电压上升率（RRRV）与限流比（0.1≤α≤1）的关系曲线，如图7-6所示。

由图7-6的计算结果可见，发生近区短路故障时，随着FCL限流比的增大，断路器的恢复电压上升率都具有先增大后减小的变化趋势。需要指出的是，若电源侧杂散电容较小，其近区故障恢复电压将会相应较大。因此，对断路器开断近区故障而言，安装FCL后并不一定导致开断难度的增加，还要看限流比的大小。此结果可在选择合适的限流比时作为参考。比较图7-3和图7-6中的结果可见，近区故障的开断要明显难于FCL出口短路故障，尽管后者的短路电流较大。

同理，分别考虑C_s=1.5μF和C_s=0.05μF两种情况并取限流比α为0.3、0.6、0.9时，可以得到恢复电压上升率与近区故障距离s的关系曲线，如图7-7所示。由图7-7可知，对于不同的限流比，断路器恢复电压上升率取得最大值所对应的近区故障距离各异。因此，最优限流比的最终选择，既要依据这些理论分析结果，还要兼顾断路器的实际开断特性。

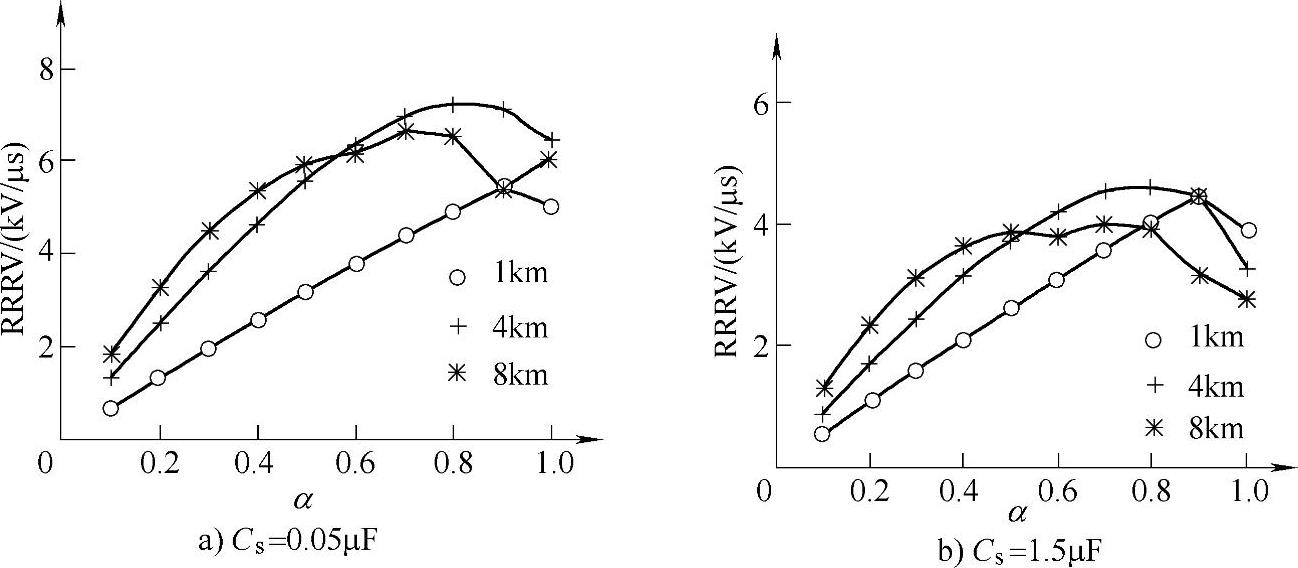
图7-6 近区故障时恢复电压上升率与限流比的关系

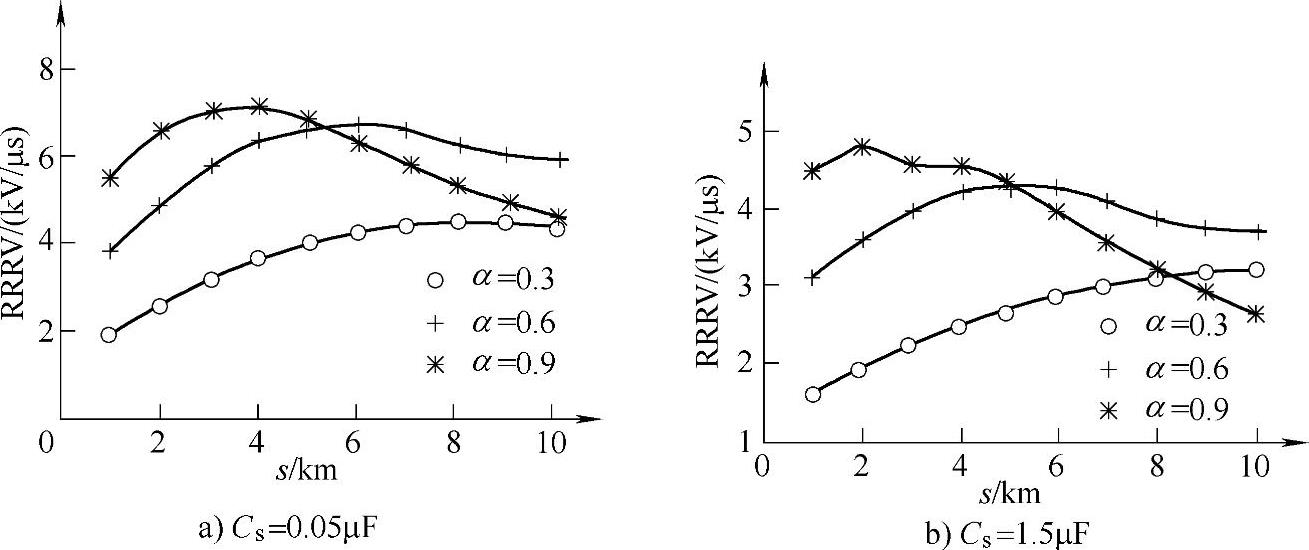
图7-7 恢复电压上升率与故障点距离s的关系

另外，为了证明系统发生近区故障时，电源侧电容电压振荡周期T₁、FCL限流电抗的电压振荡周期T₂、故障线路的行波电压振荡周期T₃之间的关系，通过EMTP针对近区故障仿真模型进行仿真，得到断路器两端电压变化曲线如图7-8所示，在这里，由于T₃最小，因此其决定了断路器恢复电压达到首峰值的时间。