1.大容量化参数优化研究

在大容量应用场合，系统正常和短路时的电流相差悬殊，在不改变磁性材料的前提下，PMFCL朝大容量发展，需考虑如下问题：

1）i_min是限流器发生状态转换时的重要阈值，i_min过小且接近额定电流时，可能发生误动现象；i_min过大且接近系统短路电流时，可能发生拒动现象，故必须以限流器不拒动且不误动为目标，优化限流器的结构参数；

2）PMFCL作为串联设备，应将其对系统的影响控制到最小，在限流能力不变的前提下，应确保其工作压降小于线路额定压降的5%；

3）经济成本与制造难易程度也是PMFCL结构参数优化研究中必须考虑的因素，在保证限流能力且可靠运行的条件下，应追求用料较少的参数设计方案，以适应大容量化的设计要求；此外，由于难以为大尺寸永磁体找到合适的充磁机及装配器械，在保证偏置能力的前提下，其尺寸应越小越好。

基于上述优化约束条件，对上文导出的4个参数设计公式进行改进，以期获得大容量条件下的结构参数优化方法。

如图5-22所示，曲线DABCE为正半波限流拓扑铁心工作点的轨迹，BE、AB和DA分别表示限流器的正向饱和态、退饱和态及反向饱和态。拐点A（-B_s，i_max）为铁心退饱和态与反向饱和态的分界点。系统发生故障时，铁心将进入退饱和态而开始限流。若短路电流过大，铁心工作点将越过拐点A，落入反向饱和态DA段，两绕组对外均表现为低感抗而失去限流能力，这是设计PMFCL不允许出现的情况。

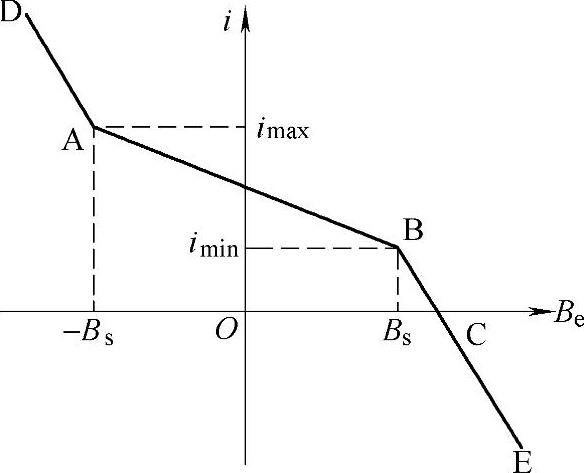
图5-22 铁心的i-B_e曲线

为避免铁心反向饱和，在设计时应留有一定裕量，同时考虑到经济成本，可将i_max设定为经限流器限制后的短路电流峰值的1.1～1.2倍。对于图5-23所示的单电源系统模型，发生短路后参数应满足

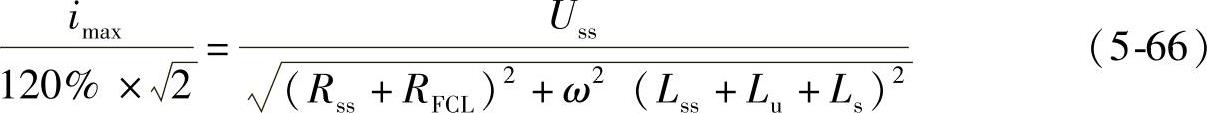
式中，U_ss为电源电压有效值；R_ss、L_ss分别为电源端的等效电阻与电感；R_FCL为限流器的等效内阻。

图5-23 串联PMFCL的单电源系统模型

将式（5-66）中的L_u+L_s定义为限流器的电感和变量ρ，其大小表征了限流能力，即

ρ=L_u+L_s （5-67）

将式（5-67）代入式（5-66），忽略电阻影响，则i_max为电感和ρ的函数，即

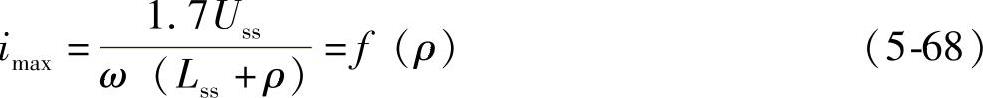
在系统参数不变时，i_max只与电感和ρ有关，且当PMFCL的限流能力越强时，i_max越小。结合图5-22可知，拐点A仅取决于电感和ρ。

图5-22中，拐点B（B_s，i_min）为铁心正向饱和态与退饱和态的分界点。通过正常工作电流时，铁心处于正向饱和状态BE段。当系统电流急剧增大时，铁心工作点将进入AB段，PMFCL开始动作而限流。

图5-22中，AB段的斜率k_AB与铁心的不饱和电感成正比，即

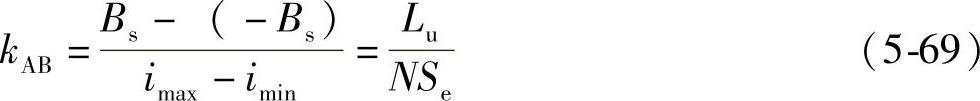
BE段斜率与铁心正向饱和时的电感成正比，即

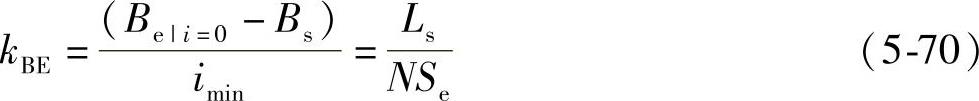
将式（5-69）除以式（5-70），并代入式（5-55），可得

以电感比变量λ置换，并代入式（5-68），可得

由式（5-72）可知，PMFCL的最小可限制电流峰值i_min由K_s、λ和ρ共同决定，即图5-22中的拐点B亦由这3个变量决定。

图5-22中，曲线DABCE与B_e轴相交于点C（B_e|i=0，0），对应绕组电流过零时，由饱和深度比变量K_s的定义可知，点C仅由K_s决定。

图5-22中的A、B、C 3点，分别由K_s、λ和ρ中的1个或几个参数决定。当确定了这3个变量后，i-B_e曲线便可确定。

根据式（5-51）、式（5-67），L_u与L_s可表示为

将式（5-73）与式（5-68）分别代入式（5-62）～式（5-65），得到

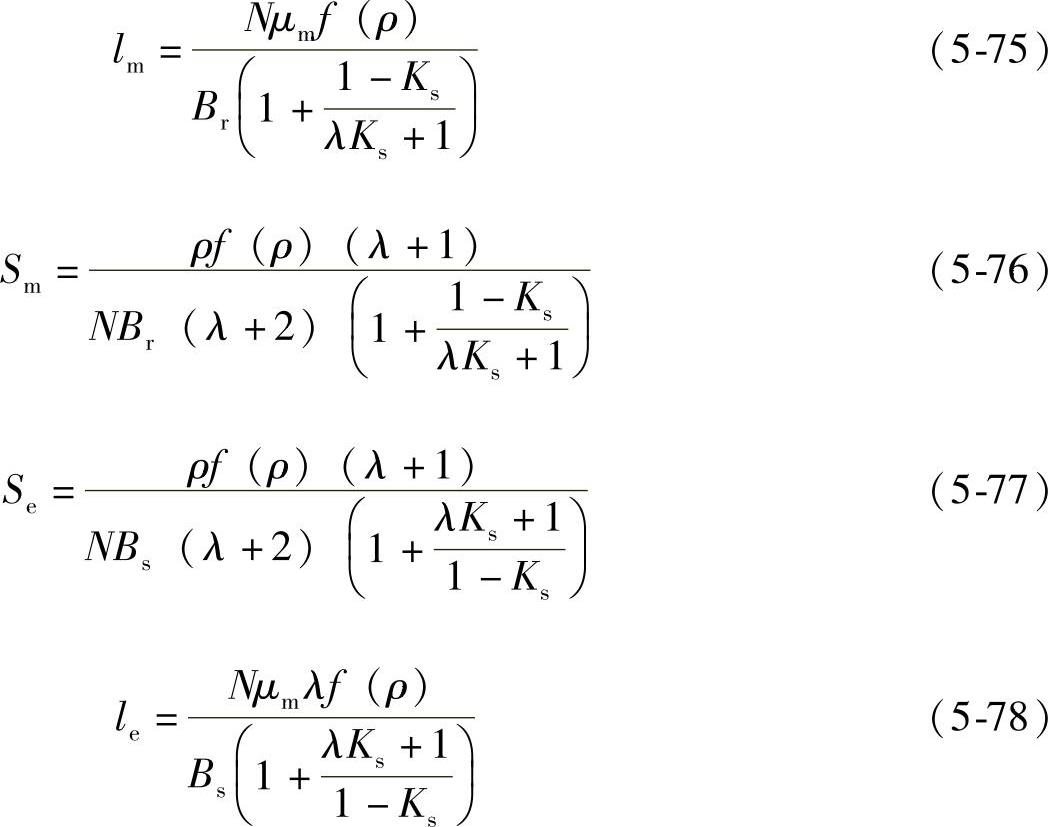
由此，PMFCL的4个关键结构参数，均可用饱和深度比K_s、电感比λ和电感和ρ3个变量来表示。因K_s、λ和ρ3个变量之间相互独立，在磁性材料及绕组匝数一定的前提下，PMFCL结构参数的优化可转化为对K_s、λ和ρ的优化，即对铁心i-B_e曲线上3个关键点的优化问题。

2.大容量化参数优化实例

针对110 kV线路发生三相接地短路时的情形进行实例分析，分析其中一相，线路模型如图5-23所示。相电压有效值U_ss为63.5 kV，电源内阻抗Z_ss为（0.85+j0.84）Ω。该线路负荷电流为1kA，预期短路电流稳态有效值为50kA。限流绕组为50匝，附加电阻为0.2Ω。铁心采用冷轧取向硅钢DW540-50，永磁体采用Nd-Fe-B材料N35，参数见表5-8。(www.daowen.com)

表5-8 PMFCL中磁性材料参数

（续）

（1）电感比变量对结构参数的影响

电感比变量λ表征限流器电抗在铁心正向饱和态与不饱和态之间的转换能力，λ与限流能力无关。设PMFCL可将短路电流从50kA限制到25kA，则i_max=120%×2×25kA=42.4kA；再根据式（5-68），得总限流电感ρ为4.8mH。设B_e|i=0^为2.1T，则饱和深度比K_s为15.2%。

保持K_s和ρ不变，分别将λ=0.5、1、2、…、7共8组数据代入式（5-75）、（5-78）中，得到表5-9所示的PMFCL结构参数与电感比的关系，每一列对应一种结构参数设计方案。由表5-9可知，随着λ增大，永磁体厚度与截面积均有所增加，铁心截面积呈先增后减的趋势，但总体影响不大。铁心长度受λ影响最大，在电感比变化区间内，l_e增加了近70m。

表5-9 PMFCL结构参数与电感比的关系

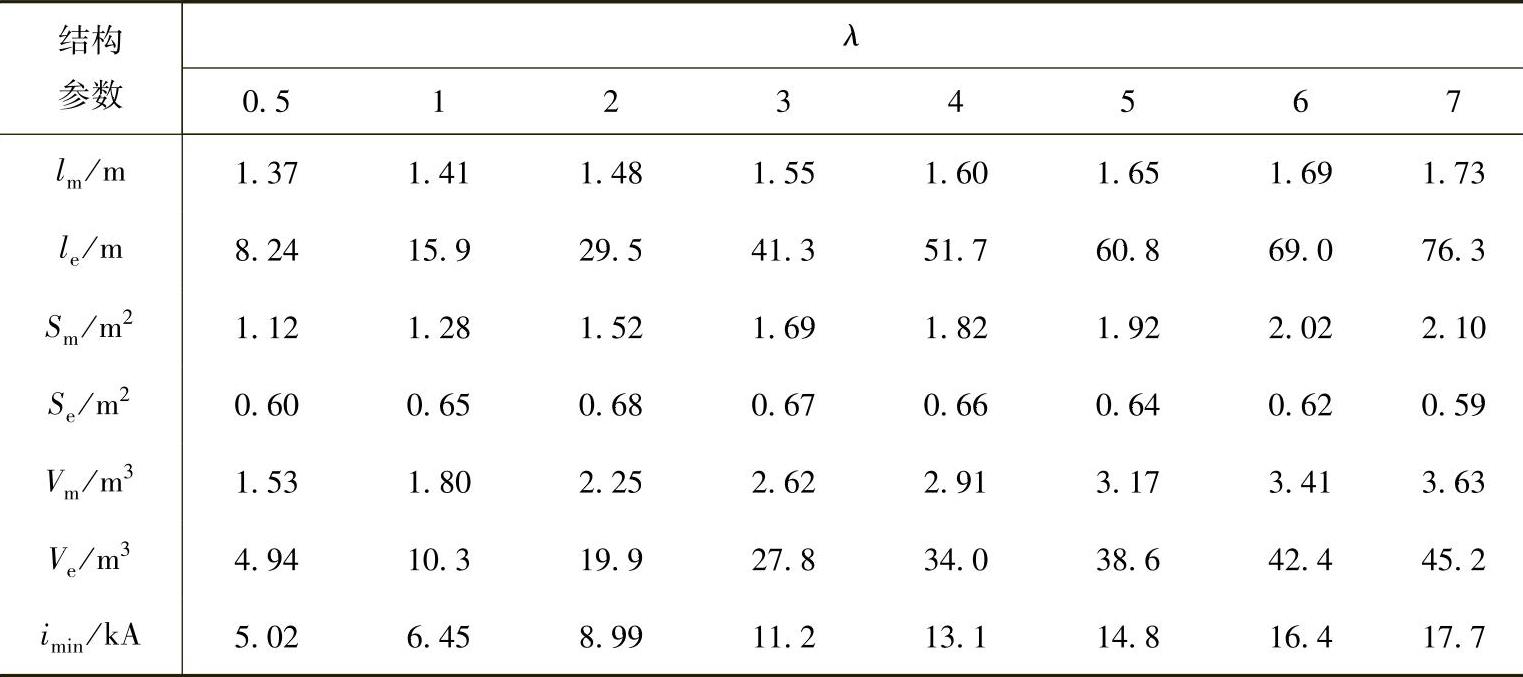
λ=0.5、7两种设计方案下的i-B_e曲线如图5-24所示。由图5-24可见，两条曲线均经过点A，表明两设计方案的限流能力相同；两条曲线均经过点C，表明虽然两方案采用不同厚度的永磁体，但两者偏置能力却完全一致。随着λ增加，铁心的饱和电感L_s逐渐减小而不饱和电感L_u逐渐增大，使i-B_e曲线的点B向点B′移动，并使i_min也随之增大。

根据直线式PMFCL的拓扑结构特点，磁性材料的用量可用其体积来衡量，即

V_m=l_mS_m，V_e=l_eS_e （5-79）

由表5-9可知，λ对铁心材料的用料影响最大，λ越大，则需要更多的铁心材料以维持内部电感L_u与L_s的转换，从经济角度考虑不可取；但λ也不能太小，当λ=0.5时，虽然i_min仍高于系统额定电流，但此时限流电抗上的正常工作压降U/U_ss=3.97%，接近5%，对系统的影响已不可忽略。综合考虑，将λ=1作为电感比的最优值，此时限流电抗上的正常工作压降U/U_ss=1.78%。

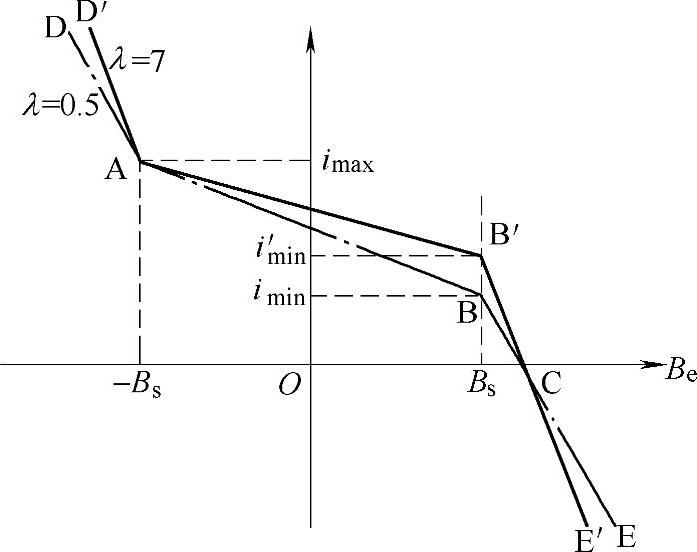
图5-24 不同电感比的i-B_e曲线

（2）饱和深度比变量对结构参数的影响

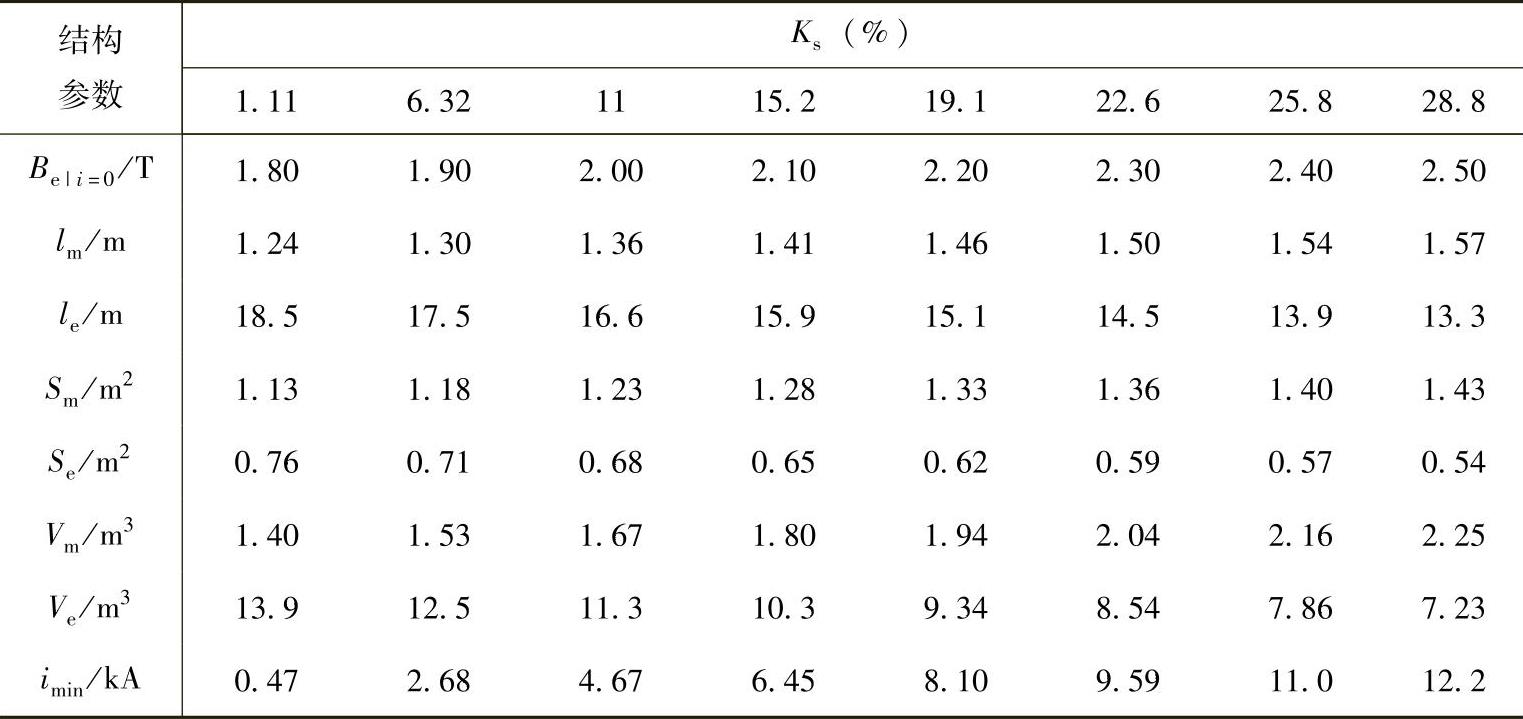
饱和深度比K_s表征PMFCL中永磁体对铁心的磁偏置能力。这里，电感比采用最优值λ=1，电感和仍为4.8mH。保持λ和ρ不变，分别将K_s=1.11%～28.8%共8组数据代入式（5-75）～式（5-78）中，所得结果见表5-10。由表5-10可以看出，随着K_s增大，永磁体厚度与截面积均有所增加，铁心长度与截面积有所减少，但总体来看，饱和深度比对磁性材料的影响不大。

表5-10 PMFCL结构参数与饱和深度比变量的关系

K_s=1.11%、28.8%两种设计方案下的i-B_e曲线如图5-25所示。由图5-25可见，两条曲线均经过点A，说明两设计方案的限流能力相同。根据式（5-72）可知，随着K_s的减小，i-B_e曲线的点B′将沿虚线向点B移动，使得i_min也随之减小；但K_s也不宜太小，如K_s=1.11%与K_s=6.32%两组中的i_min均接近系统额定电流，不利于PMFCL可靠运行。综合表5-10所示的计算结果，当K_s=11%时，i_min大小较合适，且经济性能优异，可作为饱和深度比的最优值。

（3）电感和变量对结构参数的影响

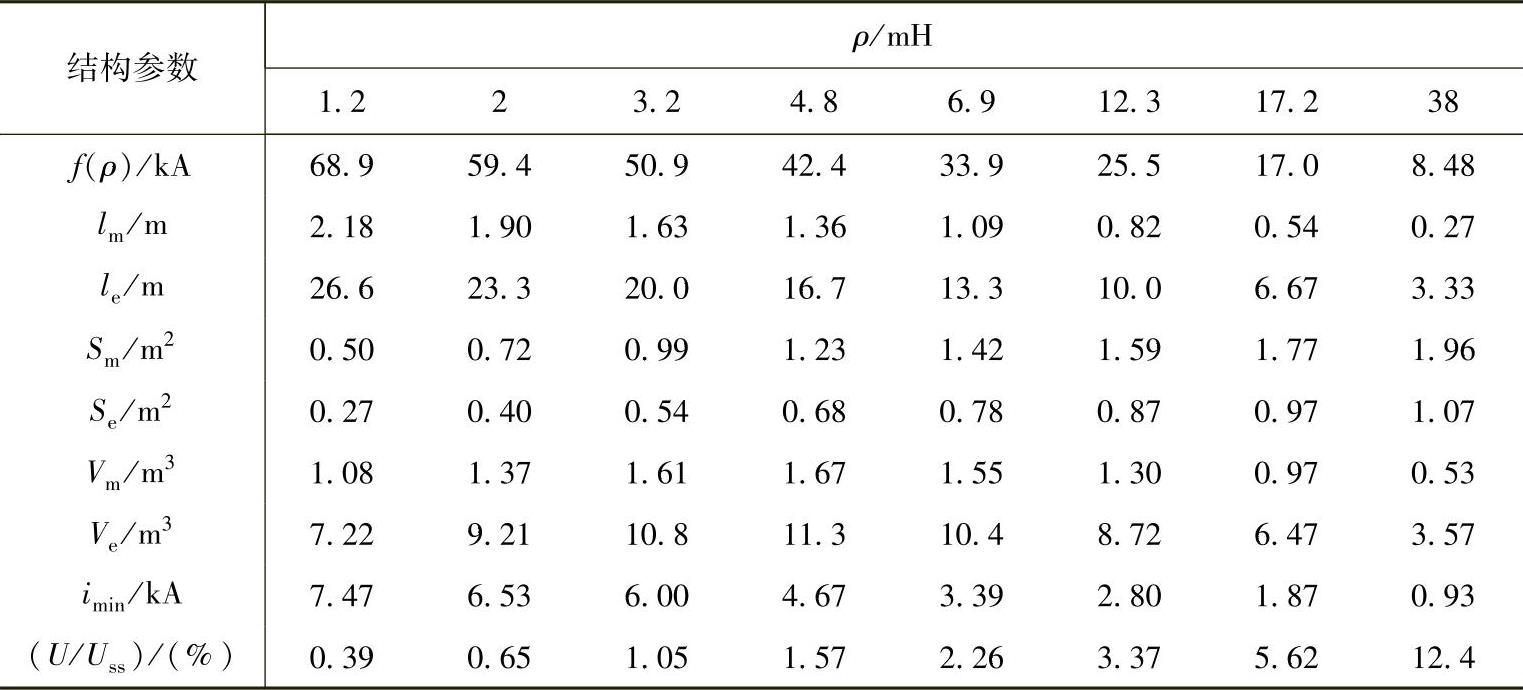
电感和ρ表征PMFCL的限流能力。这里，电感比与饱和深度比分别采用上文分析的最优值λ=1与K_s=11%。保持λ和K_s不变，将ρ=1.2～38mH共8组数据代入式（5-75）～式（5-78）中，结果见表5-11。由表5-11可见，随着ρ增加，永磁体与铁心的长度参数均呈递减趋势，而截面积参数则呈现递增趋势。

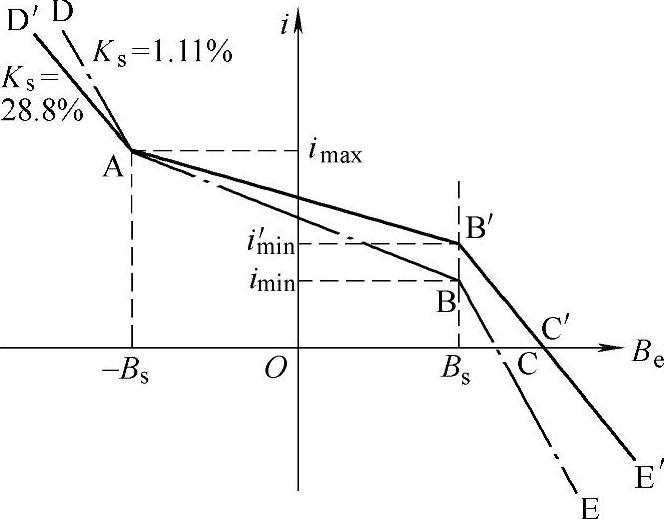
图5-25 不同饱和深度比的i-B_e曲线

表5-11 PMFCL结构参数与电感和变量的关系

ρ=1.2mH、38mH两种设计方案下的i-B_e曲线如图5-26所示。由图5-26可见，随ρ增加，点A沿虚线向A′移动（参见式（5-68）、式（5-72）），又因f（ρ）与i_min成正比，使点B向B′移动；两曲线均过点C，说明两限流方案的磁偏置能力相同。

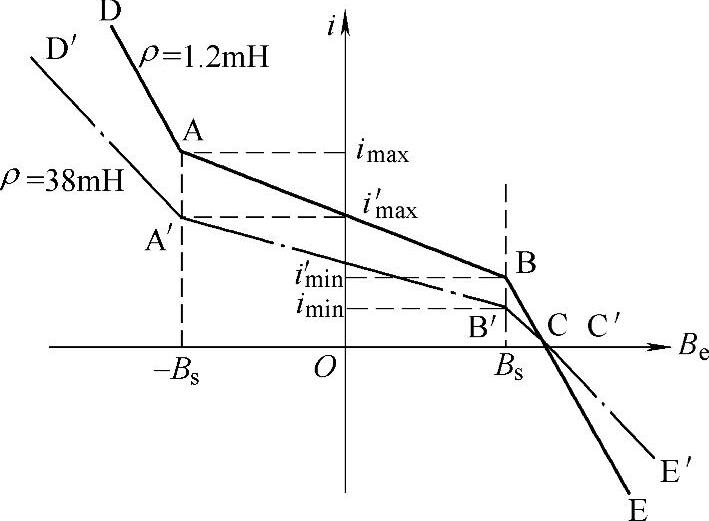
图5-26 不同电感和的i-B_e曲线

随着ρ增大，正常工作压降U/U_ss也随之增加，当ρ=17.2mH时，U/U_ss已超过设计限流器所允许的最大值5%。另外，铁心与永磁体的用量V_e与V_m均呈现先增后减的趋势，且在ρ=4.8mH左右出现极大值。同时，当ρ>6.9mH后，i_min也将接近系统额定电流。综合考虑大尺寸永磁体经济性以及制造难度，取ρ=6.9mH作为最优值。

3.仿真验证

根据上述设计实例，得到110kV系统PMFCL的最优变量组合为：λ=1，K_s=11%，ρ=4.8mH。由此算得的结构参数为：l_m=1.09m，l_e=13.3m，S_m=1.42m²，S_e=0.78m²。为验证提出的结构参数优化算法及设计实例结果的合理性，采用ANSOFT Maxwell-2D软件建立了基于有限元的直线式PMFCL的场-路耦合仿真模型，获得了永磁体与软磁铁心的磁场分布图。图5-27为短路发生后在第一个半波的短路电流峰值时PMFCL的磁感应强度分布。线段AB的磁感应强度分布如图5-28所示，由图5-27和图5-28可知，此时被绕组线圈包围的铁心磁感应强度约为1.78T，接近反向饱和状态。仿真结果验证了参数优化算法的有效性。

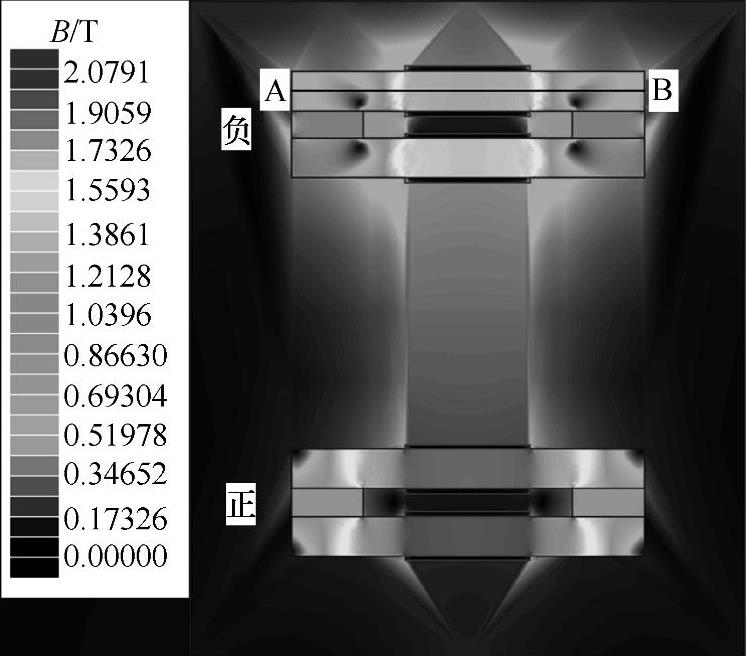
图5-27 PMFCL磁感应强度分布图

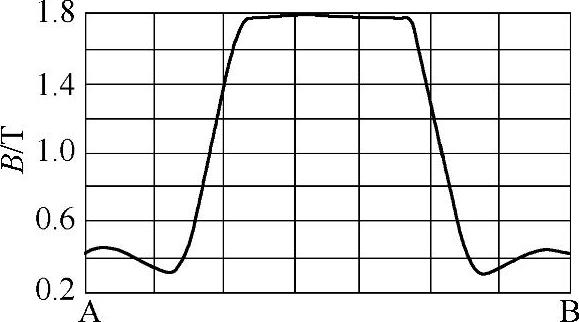
图5-28 铁心AB段磁感应强度