迄今，国内外学者已对永磁饱和型故障限流器（PMFCL）开展了仿真和实验研究，并研制了不同拓扑结构的永磁饱和型故障限流器样机。然而这些研究多集中于低压小短路电流场合，在高压大容量化方面尚未形成系统的结构参数设计方法，也缺乏面向大容量应用的结构参数优化方案。文献[3，4]提出了一种永磁并联偏置方式的“日”字型磁路结构，文献[5，6]提出了一种永磁串联偏置方式的“口”字型磁路拓扑。文献[7]提出了2个环形铁心夹2片永磁体的新结构，并设计了220 V实验样机。文献[8，9]提出了一种直线式PMFCL拓扑结构（参见图5-20），它包括两对相互配合的铁心和缠绕在铁心上的铜绕组，而在每对铁心的两端各置有一块永磁体，且采用左右两组分别限制正、负半波的短路电流。相比于传统的PMFCL限流拓扑，直线式PMFCL更加简洁经济，便于加工制造；此外，该结构的永磁体与铁心截面积参数保持相对独立，为后续结构参数的优化研究提供了有效的技术途径。文献[9]亦从温度、外磁场两方面分析了钕铁硼永磁体的稳定性问题，论证了其应用到PMFCL的可行性。

针对直线式PMFCL磁拓扑，基于等效磁路法研究了一种直线式PMFCL面向高压大容量化的结构参数设计算法；提出饱和深度比、电感比以及电感和3个重要变量的定义，并推导出描述参数关系的归一化数学表达式；藉此将该PMF-CL结构参数的优化转化为对以上3个变量的优化问题，最后通过基于有限元的场-路耦合仿真对分析结果加以验证。

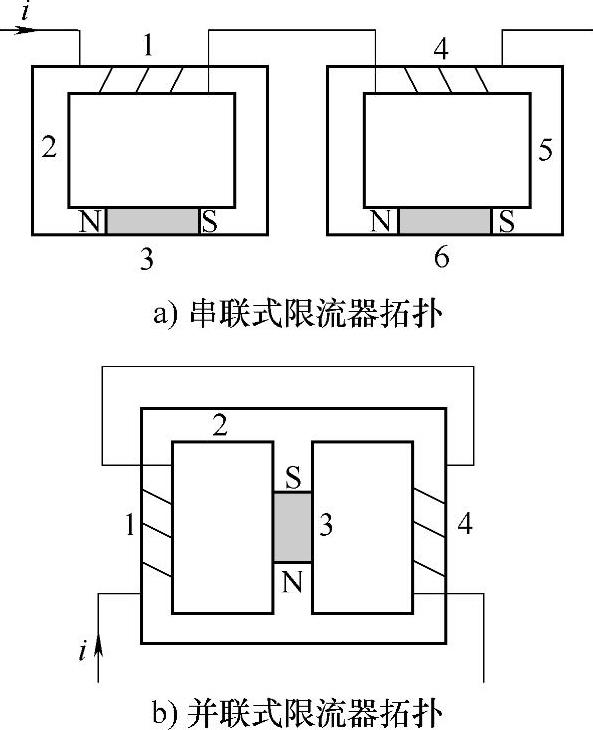
图5-19 永磁饱和型故障限流器的拓扑原理图

1，4—绕组 2，5—铁心 3，6—永磁体

按照永磁体与软磁铁心组成的磁路形式，可将永磁饱和型故障限流器的拓扑类型分为串联式和并联式两种。串联式拓扑由两组铁心、永磁体以及交流铜绕组构成，目的是为了在正、负半波均能限制短路电流，如图5-19a所示。并联式拓扑的左右两个分支铁心，分别用来限制短路电流的正、负半波，且共用同一永磁体产生偏置磁场，如图5-19b所示。

无论是串联式还是并联式，交流铜绕组全都绕制在铁心上，其中一个绕组产生的磁动势与永磁体相同，另一绕组则相反。两个绕组串接后与输电线路串联。当系统正常工作时，永磁体产生的很强的直流偏置磁场，可使铁心处于深度饱和状态。此时，额定电流通过绕组产生的交变磁场不足以使铁心脱离饱和区域，该绕组表现为低感抗状态，限流器对系统的影响很小；当系统出现短路故障时，瞬间增大的电流使绕组产生的磁动势足够抵消永磁体的磁动势，限流器的某一组铁心的工作点将从饱和区进入线性区域，使绕组产生很大的感应电动势，对外表现为高阻抗，从而限制了短路电流；若短路电流继续增大到某一值时，交变电流产生的磁动势有可能使铁心进入反向饱和状态，此时限流器则失去限流能力。

由上文原理介绍可知，永磁体对外提供直流偏置磁场的能力，即永磁体偏置能力的强弱，是限流器能否正常工作的关键因素。传统限流拓扑的铁心用量较多，而永磁体占的比重很小，这导致铁心在系统正常工作时难以深度饱和，而短路大电流时又容易反向饱和，造成限流器的工作性能较差。

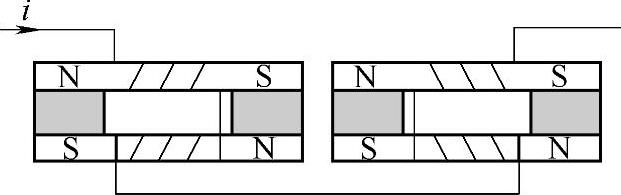
图5-20 直线式PMFCL拓扑示意

提出一种直线式PMFCL拓扑，如图5-20所示。该结构包括一对相互配合的铁心，在铁心的两端分别设有一个永磁体，在两铁心上还分别绕有铜线绕组。左右两组分别用来限制正、负半波短路电流。与串联式拓扑相比，新型拓扑省去了为构成磁路而需要的截面积较大的铁心部分，结构更加简洁经济，便于加工制造；与并联式拓扑相比，新型拓扑增加了永磁体在限流器中的比重，有利于改进永磁体的偏置能力。更重要的是，新型拓扑中铁心与永磁体的结构参数可任意调节，有利于改进永磁体的偏置能力，为限流器的高压大容量化提供了有效的技术途径。开展的仿真与实验工作，均基于该种直线式PMFCL拓扑。

构成直线式PMFCL结构参数设计算法的基本思路是：基于等效磁路法，并依据永磁体、软磁铁心的相关磁参数以及线路条件，导出PMFCL的关键结构参数l_m、l_e、S_m和S_e的数学表达式。

为了便于表述，表5-7给出所用的主要符号及其释义。

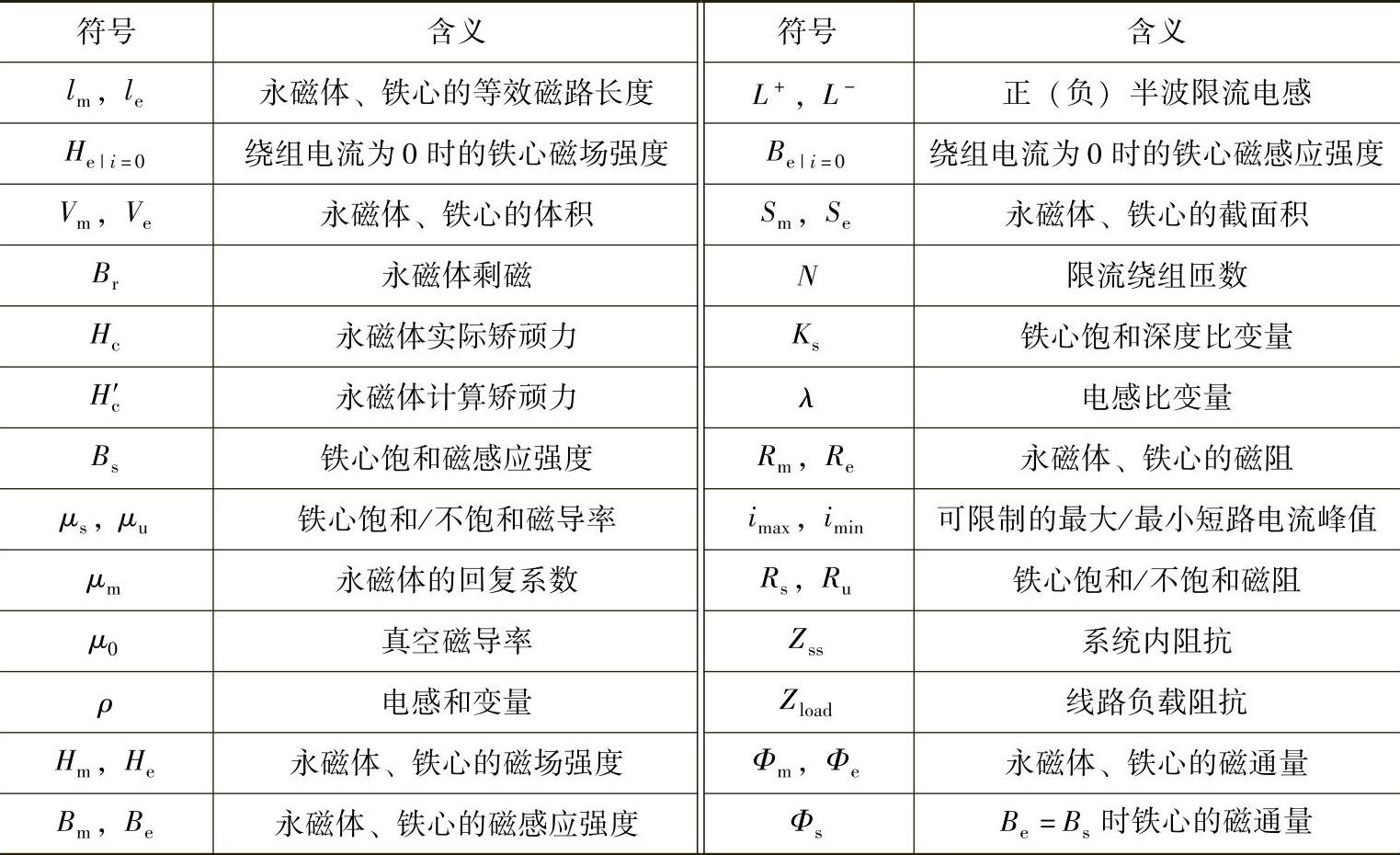
表5-7 主要符号的含义

为简化分析，作如下假设：①磁场在永磁体与铁心内分布均匀，且不考虑漏磁场；②采用三折线型的铁心B-H曲线，如图5-21中曲线I所示，忽略铁心磁滞效应；③各媒质均为各向同性材料，且忽略时变场频率ω的影响。

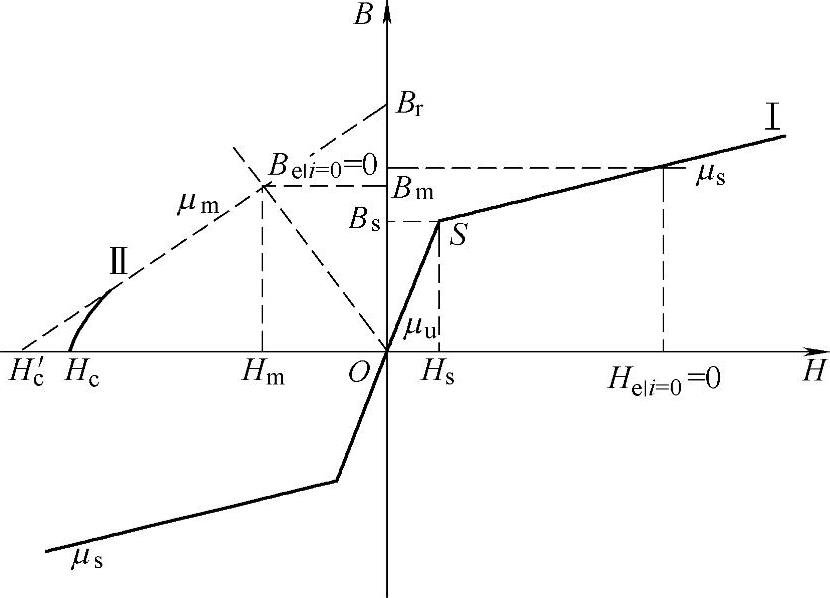
图5-21 永磁体与铁心的B-H曲线

以直线式PMFCL中限制正半波短路电流的过程为例，应用安培环路定理可得

Ni-H_c′l_m+R_mΦ_m+H_cl_e=0 （5-40）

式中，R_m=l_m/（μ_mS_m）；H′_c=B_r/μ_m。因钕铁硼（Nd-Fe-B）材料的计算矫顽力H_c′与其实际矫顽力H_c相差不大，可认为两者近似相等。

由磁通连续性原理可知，通过永磁体的磁通量可用通过铁心的磁通量来表示：

Φ_m=Φ_e （5-41）

因PMFCL串联于工频交流系统中，故式（5-40）中的磁场强度H_e、磁通量Φ_e以及电流i均为时间t的交变函数，而永磁体的磁动势分量-H_c′l_m与t无关。将式（5-41）代入式（5-40）并对t求导，可得

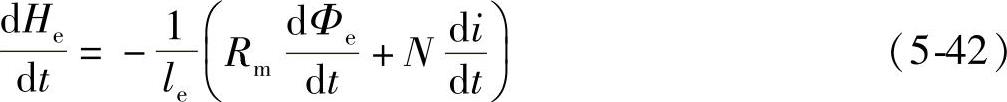
磁通量Φ_e与磁场强度H_e存在如下关系：

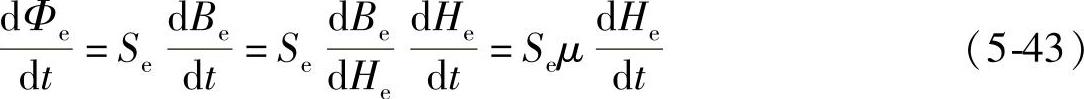
将式（5-43）代入式（5-42），并依据法拉第电磁感应定律，可得限流绕组的感应电压u为

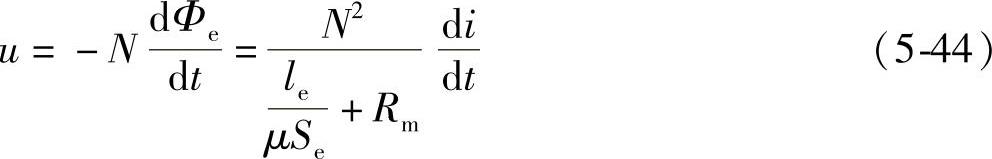
式中，μ为铁心磁导率。

由工作原理知，PMFCL的总电感L_PMFCL为正、负半波限流拓扑电感之和。正半波的限流电感L+（负半波限流电感L-与L+相同）可由式（5-44）得出

系统正常工作时，正、负半波限流拓扑均处于饱和状态，即_μ=μ_s。定义L_s为铁心饱和时半波限流器的电感，此时限流器的总电感L_PMFCL为

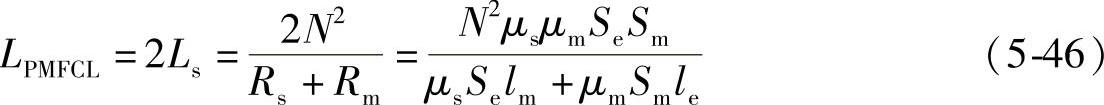
式中，R_s=l_e/（μ_sS_e）。故铁心饱和时的半波限流器的电感L_s为

当系统发生短路时，PMFCL必有一组限流拓扑退出饱和，另一组仍处于饱和状态。设退出饱和的铁心磁导率为_μu（参见图5-23），定义L_u为铁心不饱和时半波限流拓扑的电感，则整个限流器的电感L_PMFCL可写为(www.daowen.com)

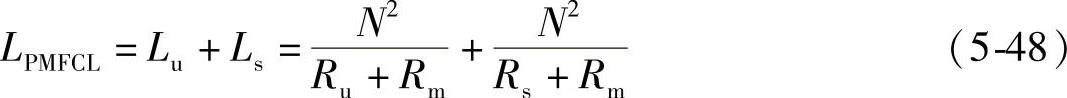
式中，R_u=l_e/（μ_uS_e）。故铁心不饱和时半波限流拓扑的电感为

因μ_u>>μ_m，R_u<<R_m，此时可忽略R_u，则L_u可改写为

定义λ为PMFCL的电感比变量，即

式中，L_u>L_s，故λ>0。

将式（5-47）、式（5-50）代入式（5-51），可得铁心与永磁体长度之比（l_e/l_m）与截面积之比（S_e/S_m）的关系为

根据图5-21中的曲线I，当铁心的工作点位于饱和区时，其磁场强度可表示为

当电流过零时无需考虑绕组影响，PMFCL的磁路可等效为永磁体与铁心组成的永磁磁路。将式（5-53）代入式（5-40），令i=0，忽略R_u，整理可得

（B_e|i=0-B_s）S_ers+B_e|i=0S_er_m=Hc′l_m （5-54）

为描述永磁体偏置作用下的铁心饱和程度，定义K_s为饱和深度比变量，则有

式中，B_e|i=0>B_s，故0<K_s<1。

将式（5-55）代入式（5-54），并代入H_c′=B_r/μ_m，得

整理后得S_e/S_m与电感比、饱和深度比两变量的数量关系如下：

根据PMFCL工作原理，当Φ_e=Φ_s=B_sS_e时，铁心刚好退出正向饱和状态而开始限流，此时的电流为限流器可限制的最小短路电流，以i_min表征其峰值，代入式（5-40），并忽略R_u，可得

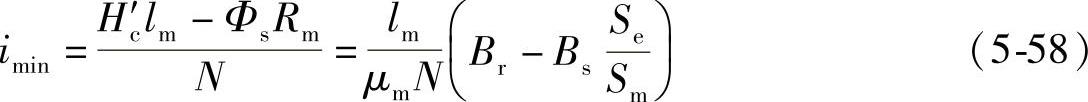
当Φ_e=-Φ_s=-B_sS_e时，铁心刚好进入反向饱和态，限流器恰好失去限流能力，此时的电流为限流器可限制的最大短路电流，以i_max表征其峰值，代入式（5-40），并忽略R_u，可得

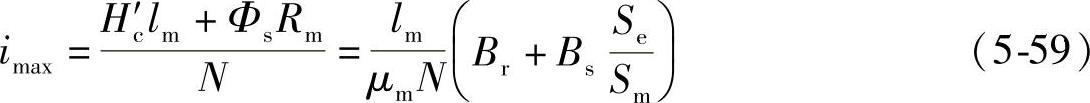
进而得到式（5-59）与式（5-58）的商与差为

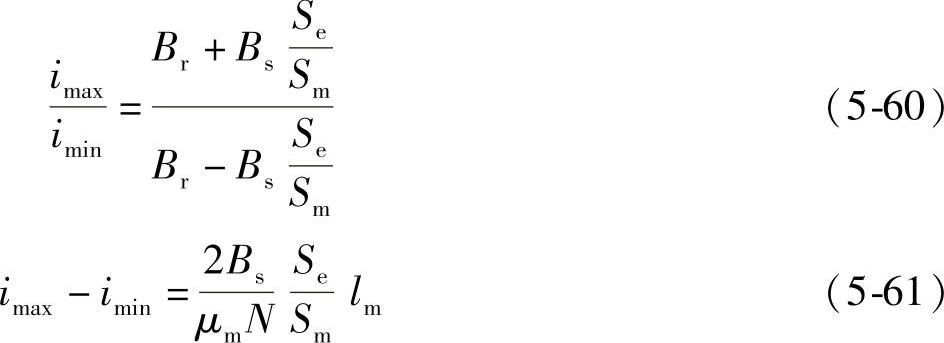
将式（5-57）分别代入式（5-60）、式（5-61），消去S_e/S_m与i_min，可得永磁体长度的表达式为

将式（5-62）代入式（5-60），得永磁体截面积为

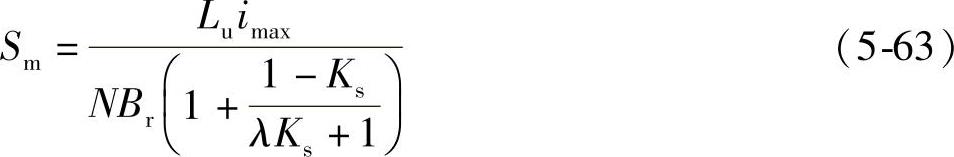
将式（5-63）代入式（5-57），得铁心截面积表达式为

将式（5-62）代入式（5-52），得铁心长度表达式为

式（5-62）～式（5-65）构成了优化PMFCL关键结构参数的基本数量关系方程。