1.静态磁场分析
永磁饱和型故障限流器要达到理想的限流效果,磁性能极为重要,既要使铁心达到饱和状态,又要尽量减少空气中的漏磁。其中,铁心的饱和程度的高低直接决定限流器的限流容量。用ANSOFT Maxwell-2D有限元软件对四种结构的磁场进行了详细分析。
限流器绕组通过电流为零时,静态磁场的磁感应强度的分布如图5-6所示。四种拓扑的限流器绕组铁心均已经进入饱和状态,大约在1.75~2.2T之间;永磁体的磁感应强度较低,在0.65~1.2T之间。由于永磁体的剩磁小于铁心的饱和磁感应强度,磁通方向与永磁体一致,因此,靠近永磁体的部分铁心无法达到饱和。另外,口字型和直线型的铁心结构一样,因此绕组通过电流为零时,铁心磁路特性完全相同。
当绕组中没有电流通过时,绕组缠绕的铁心、PMFCL永磁体中的静态磁感应强度变化规律如图5-7所示。
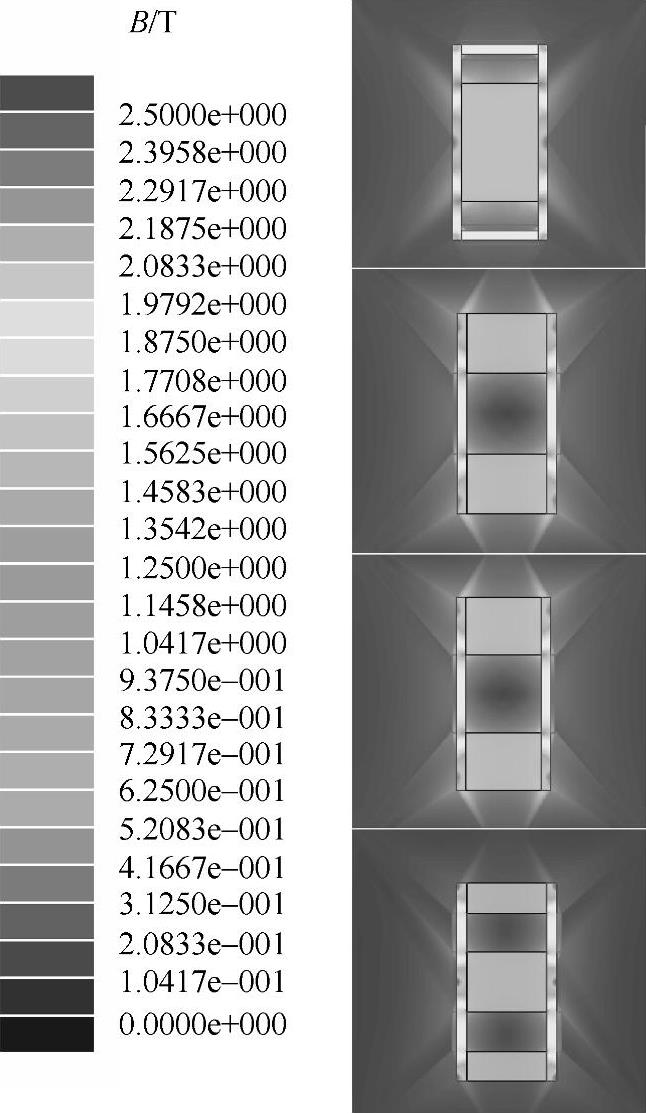
图5-6 PMFCL拓扑铁心的静态磁感应强度分布
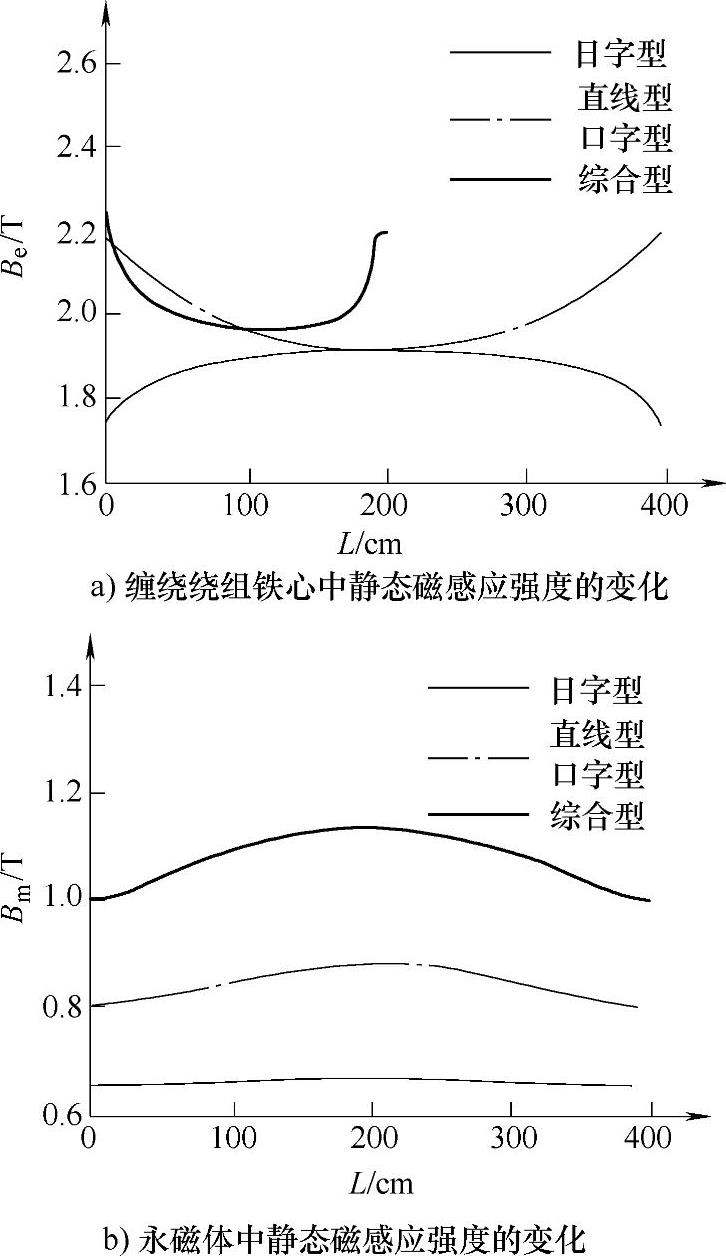
图5-7 不同拓扑PMFCL静态磁场强度的变化
由图5-7a可知,综合型PMFCL绕组铁心饱和程度最高,其绕组铁心中磁感应饱和强度最大值为2.24T,最小值为1.96T,铁心已经进入深度饱和状态。口字型和直线型静态磁路结构完全一致,因此铁心的饱和深度系数变化规律相同,其最大值和最小值略小于综合型。综合型、口字型和直线型铁心饱和深度均呈现中间部位最小,两端最大的变化趋势。但是日字型恰好相反,中间部位磁感应强度最大为1.92T,两端最小为1.75T。因此,相对于日字型永磁饱和型故障限流器,其他三种故障限流器的铁心饱和深度较高,理论上更易实现高压大容量限流的目标。图5-7b反映了沿着PMFCL中永磁体的静态磁感应强度的变化规律。其中,综合型的永磁工作点最高,日字型的工作点最低。
由于铁心和永磁体中静态磁感应强度的分布并不均匀,为了更准确描述通过限流器的总体磁感应强度,提出了磁感应强度有效值的概念,定义如下:

式中,B为沿着铁心或者永磁体有效长度通过的磁感应强度;L为铁心或者永磁体的有效长度。
根据式(5-22)可以得到四种拓扑PMFCL的静态磁感应强度有效值,见表5-3。由表5-3可知,无论是在铁心中还是在永磁体中,综合型的有效磁感应强度均最大,日字型的均最小,与图5-7中结果一致,表明综合型PMFCL的铁心饱和程度较高。
表5-3 PMFCL的静态磁感应强度有效值(单位:T)

除了铁心的饱和程度以及永磁体的工作点外,磁路中还可能有漏磁现象。漏磁通的大小也直接影响拓扑的磁性能,从而间接影响故障限流器的限流特性。漏磁通的计算公式如下:
Φk=ΦM-ΦE=BMSM-BESE (5-23)
不同拓扑故障限流器漏磁通比较如图5-8所示。综合型PMFCL的漏磁通最小,主磁路的磁场利用率最高。由以上的分析不难发现,综合型PMFCL的静态工作特性最优,有利于应用于高压大容量的场合。
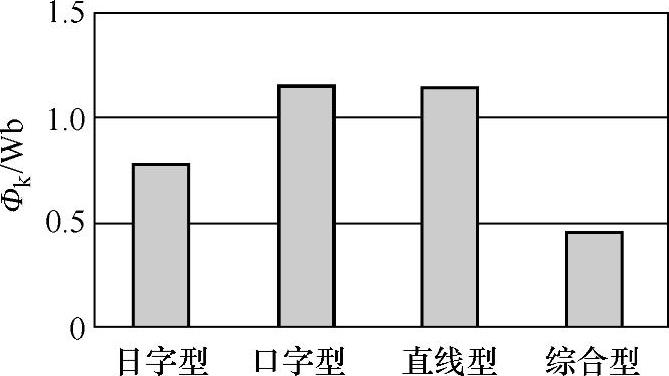
图5-8 不同拓扑PMFCL的漏磁通比较
为深入了解磁场分布规律,有必要针对铁心和永磁中的磁动势分布进行分析。而磁动势的大小与磁场强度的分布有着密切的关系。由静态计算结果,不同拓扑PMFCL中永磁和软磁铁心中的磁场强度分布如图5-9所示。由图可知,四种限流器铁心和永磁体中的磁场强度分布并不均匀,特别是通过日字型铁心直角拐弯处测量到的磁场强度很小,导致铁心的利用率很低。因此,在限流器拓扑优化设计的过程中要尽量避免铁心磁路的直角拐角,从而提高铁心的利用率。
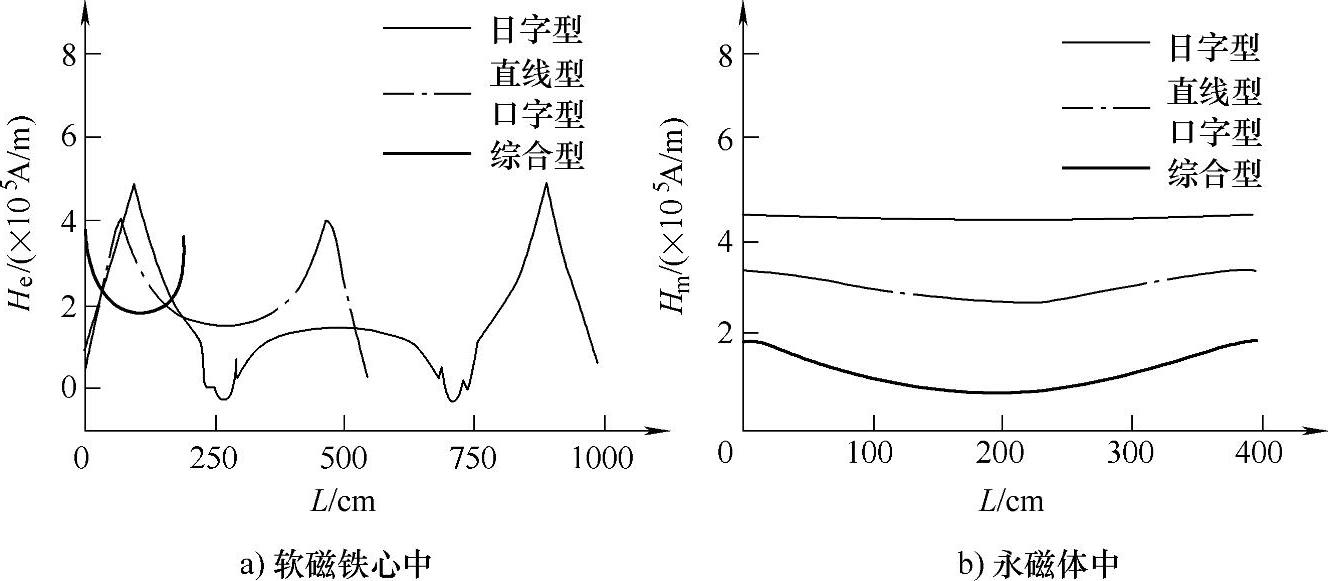
图5-9 不同拓扑故障限流器磁场强度分布
根据图5-9获得的磁场强度分布曲线数据,通过积分计算可得到永磁体上和铁心上的磁动势分别为Fm和Fe。仿真模型中永磁体和铁心上的磁动势比较,如图5-10所示。
2.静态等效磁路分析
根据图5-10且忽略计算误差,永磁体上的磁动势与铁心上的磁动势基本相等。通过以上对磁路磁通和磁动势的分析结果,可以得到四种不同限流拓扑的静态等效磁路方程。
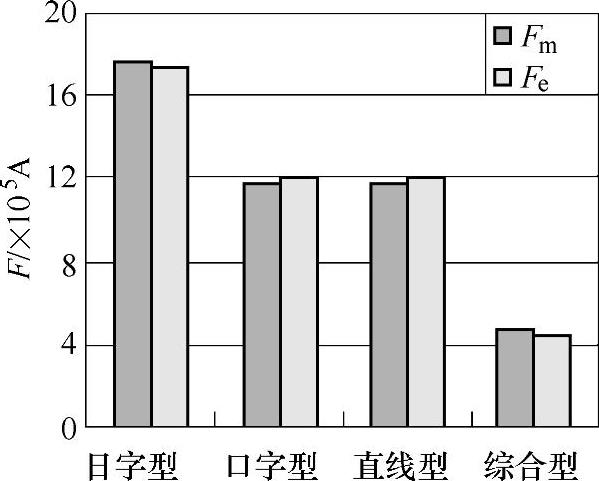
图5-10 不同拓扑PMFCL永磁体和铁心磁动势比较
为使以下公式的推导过程清晰,现将使用的数学符号及其释义列举如下:
l——等效磁路长度;
S——截面积;(www.daowen.com)
B——磁感应强度;
F——磁动势;
Hc——永磁体的实际矫顽力;
μm——永磁体的回复系数;
Bs——铁心的饱和磁感应强度;
μ——铁心磁导率;
N——限制正(负)半波限流器的绕组匝数;
Φ——磁通量;
r——磁阻。
其中,下标为“m”、“e”和“L”的符号分别定义为永磁体、铁心和漏磁场的参数;下标为“s”和“u”的符号分别表示为铁心处于饱和与不饱和状态时的参数;下标i=1、2、3、4代表对应拓扑的铁心或者永磁体。
首先,日字型PMFCL的静态等效磁路方程推导如下:

钕铁硼的B-H关系可由式(5-25)描述:

硅钢片的B-H关系可由式(5-26)描述:

将式(5-25)、式(5-26)代入(5-24)可得
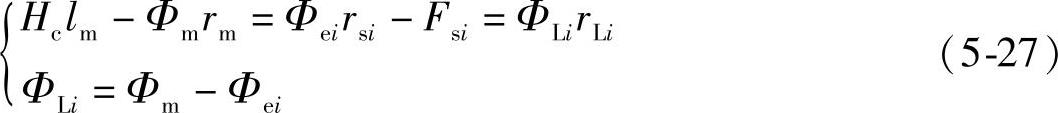
其中,
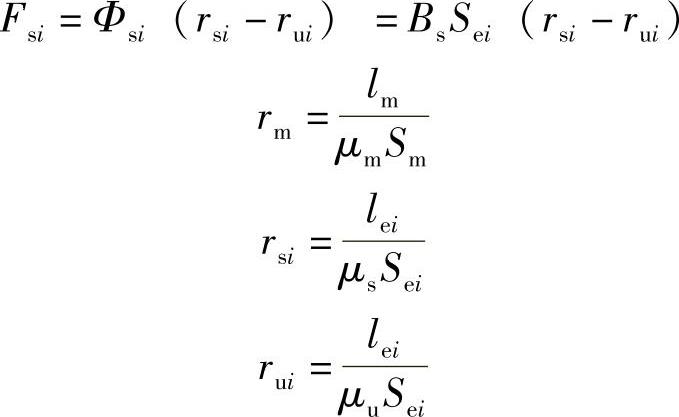
同理可得,口字型和直线型PMFCL的等效静态磁路方程如下:
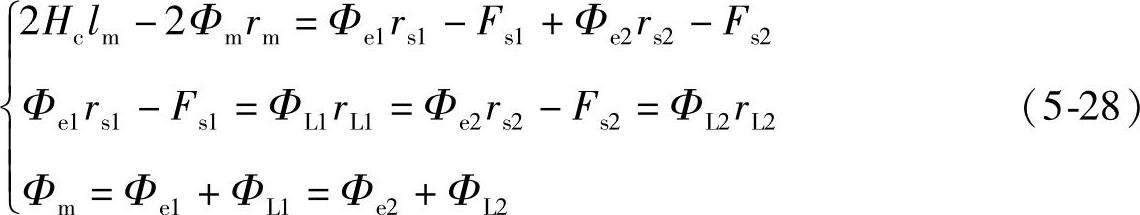
同理可得,综合型PMFCL的等效磁路方程如下:
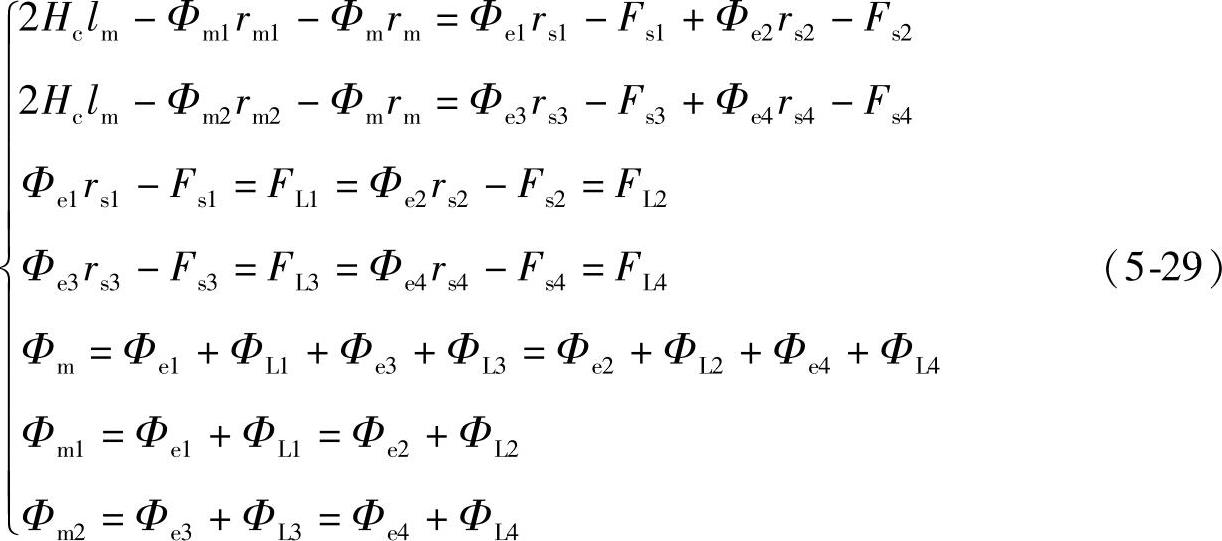
其中,
rmi=lm/(μmSmi)
因此,根据上面的式(5-27)、式(5-28)和式(5-29),可以得到四种拓扑的等效磁路结构,如图5-11所示。
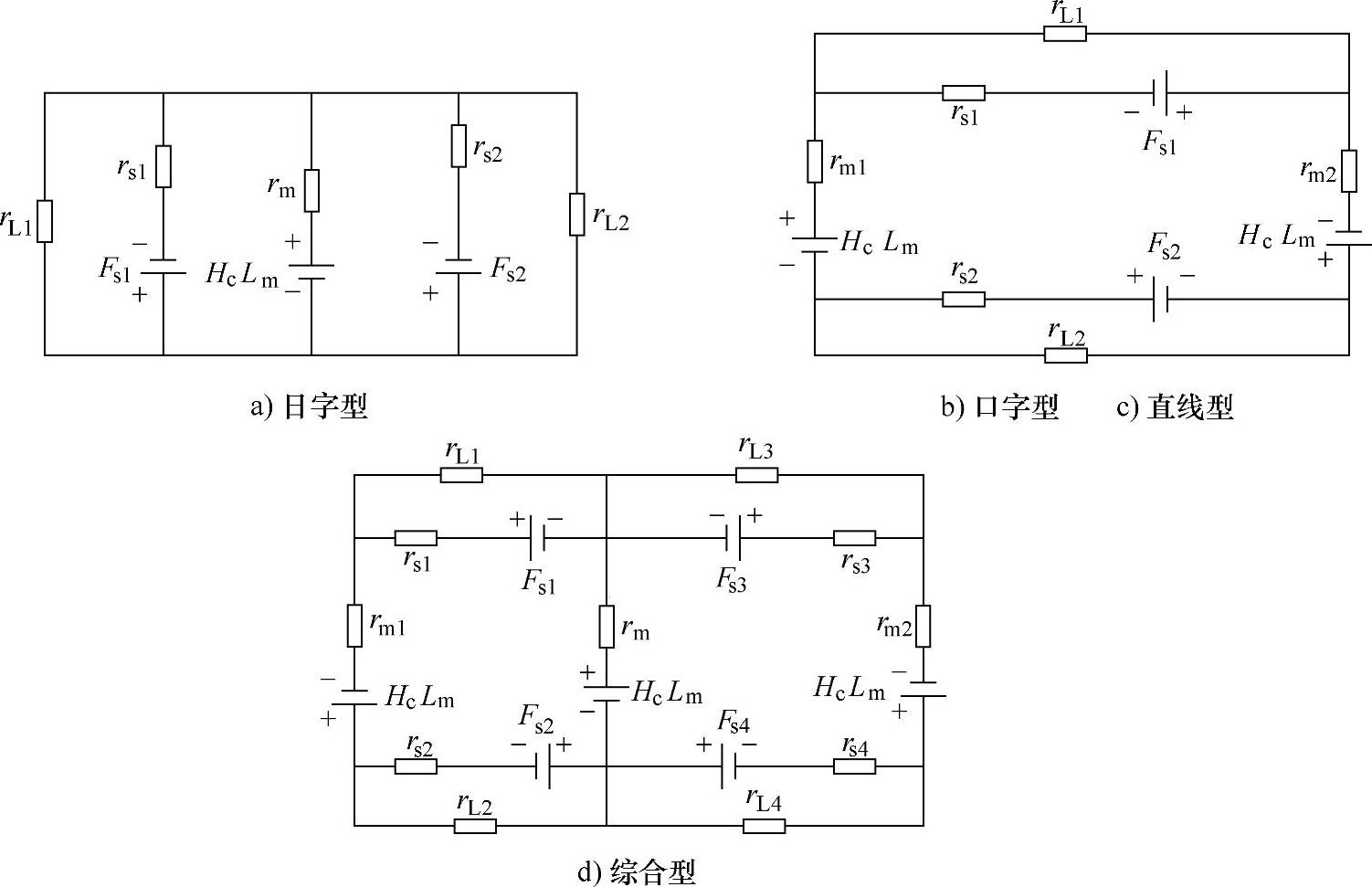
图5-11 不同拓扑PMFCL的静态等效磁路结构
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






