对于盘状推斥型电磁机构和反绕嵌套螺线管式电磁机构，其拓扑结构中均无铁心和永磁体，而由固定线圈和可动线圈组成，且其周围磁介质为各向同性、磁导率为μ₀的空气，无磁化磁场，满足叠加原理，便于进行磁场计算。

4.3.3.1 拓扑分析

图4-67 单匝线圈产生的磁场分布

首先分析单匝固定线圈通入电流后产生的磁场分布，如图4-67所示。在该磁场空间分布着均符合毕奥萨伐尔定律的闭合磁力线，这使得具有一定空间尺寸的线圈表面具有较大的径向（x方向）磁场分量。根据安培定律，处在固定线圈的上方（下方）或者外侧且与线圈平行的通流导线均会受到轴向（y方向）电磁力的作用。

进一步按两种情况分析多匝固定线圈：将单匝线圈沿径向（图4-67中x方向）增加匝数，形成水平嵌套的盘状线圈；沿轴向（y方向）增加匝数，形成垂直叠加的螺线管线圈。则可得到图4-68、图4-69所示的径向磁场分布情况（以3匝为例）。

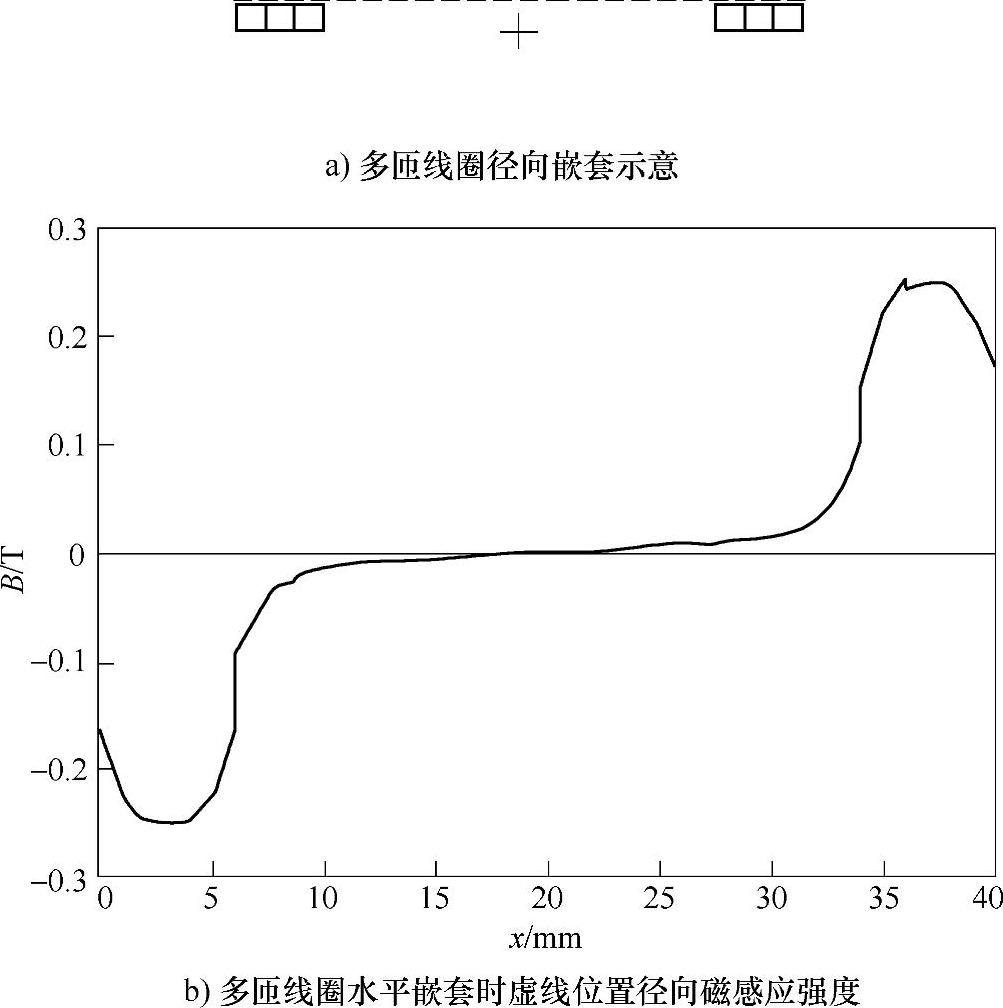
图4-68 多匝线圈径向嵌套时径向磁场分布

由此可见，只要在多个单匝线圈径向嵌套形成的盘状固定线圈上侧或下侧，放置一个与之同样的盘状线圈，则该线圈会受到向上或者向下的电磁力作用；而对于多个单匝线圈轴向叠加形成的螺线管线圈，则不能直接在其外侧嵌套与之相同的螺线管。由图4-69b可知，在固定螺线管外侧产生的磁场径向分量以螺线管高度一半处为中心，上下对称且方向相反，因此，在其外侧嵌套两个绕向相反的线圈才能产生向上或者向下的电磁力，否则其电磁力合力将为零。

4.3.3.2 计算方法分析

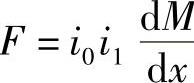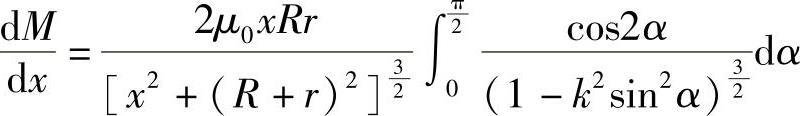由第4章中式（4-7）和式（4-8）可知，两个单匝线圈之间的电磁力为M，其中，。而根据4.2.3节中的分析方法，两个单匝线圈的电磁力计算还可进行如下分析。

将图4-10的坐标系改为轴坐标系，如图4-70所示，相应的将坐标参数x、r分别换为ρ、z。则式（4-7）可改写为

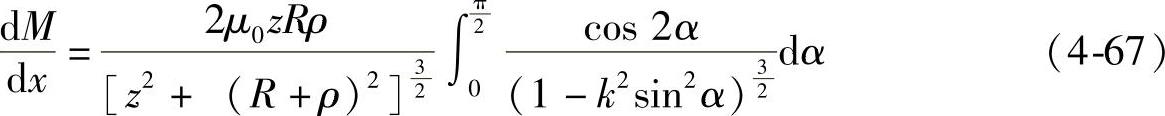
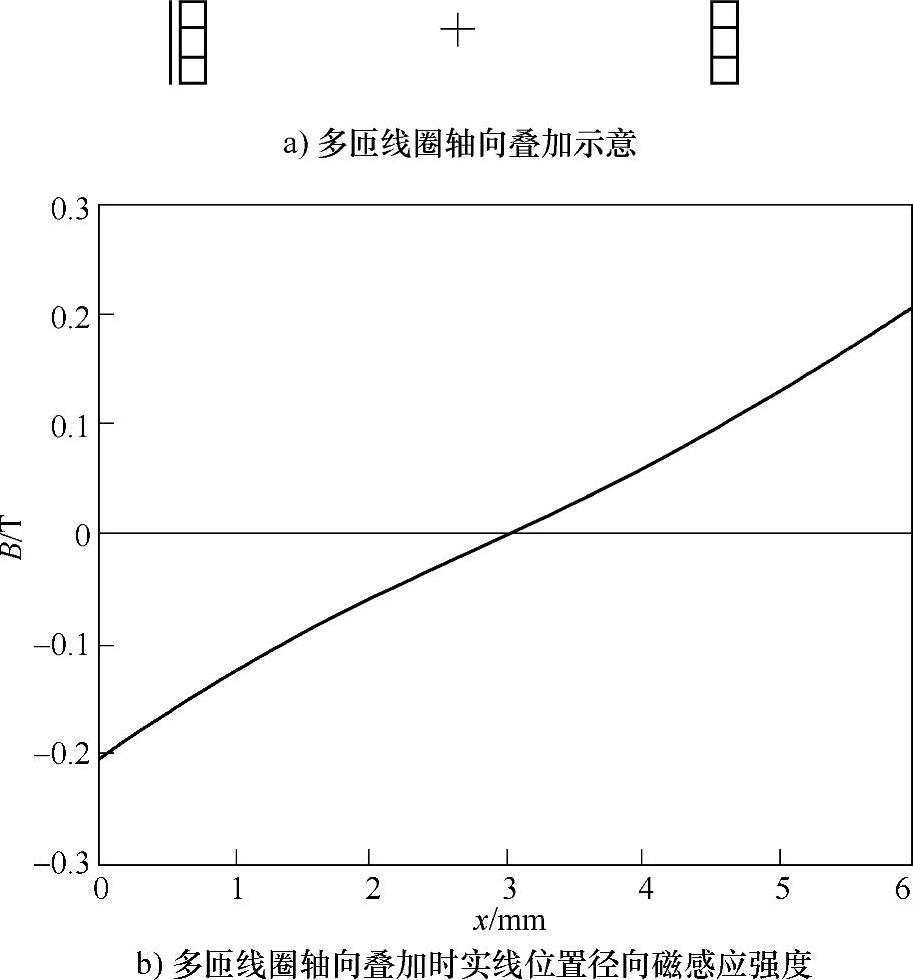
图4-69 多匝线圈轴向叠加时径向磁场分布

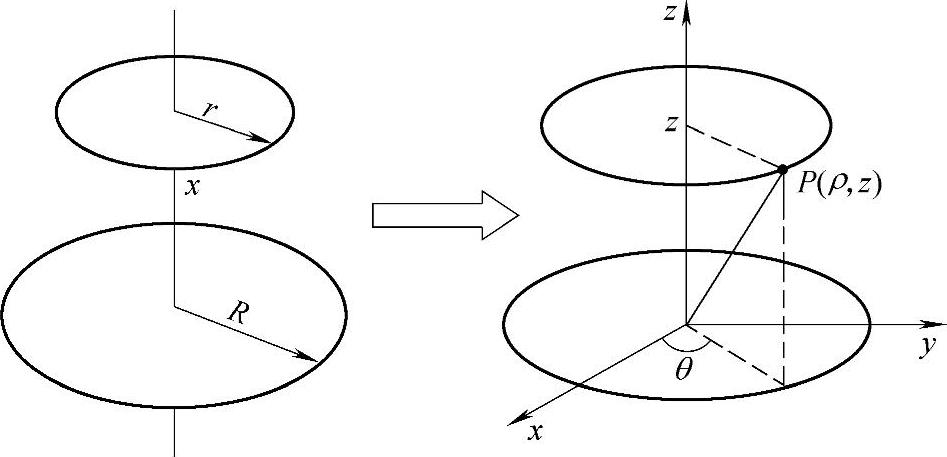
图4-70 两个单匝线圈轴坐标系示意

为分析方便起见，将第4章式（4-40）中的电流符号由I变为i₀，则式（4-40）相应地变为

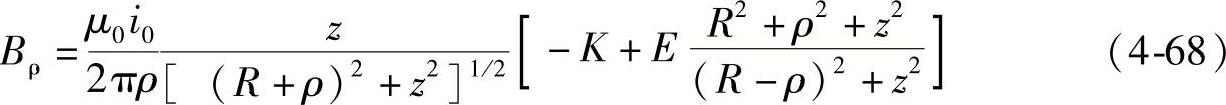
式（4-68）经推导可化成如下形式：

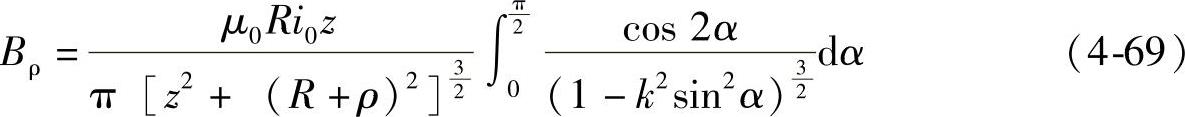
则上线圈受到的电磁力为(www.daowen.com)

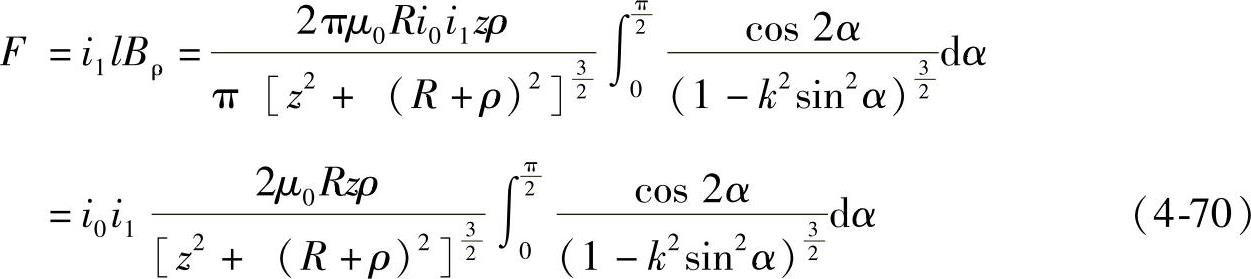
对比发现，式（4-70）与式（4-7）、式（4-8）相一致。

由此可见，无论从拓扑结构演化还是从计算方法而言，盘状推斥型电磁机构与反绕嵌套螺线管式电磁机构的动作机理可统一描述为：可动线圈切割由固定线圈产生的横向磁场分量而产生驱动电磁力。

4.3.3.3 电磁力分析

上文就两种电磁机构的拓扑关系和计算方法进行了比较分析，而对于电磁力，则可通过式（4-70）中提出的分析方法进行动态比较，但计算较为复杂。这里通过比较两者的初始静态电磁力以便于获得简洁明了的结论。

以线径截面为2mm×2mm的矩形铜导线，分别按照图4-71和图4-72的尺寸绕制盘状线圈和螺线管线圈，并能保证两者的用铜量和电阻一致，便于比较。

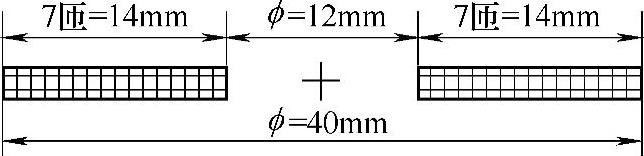
图4-71 盘状线圈尺寸示意

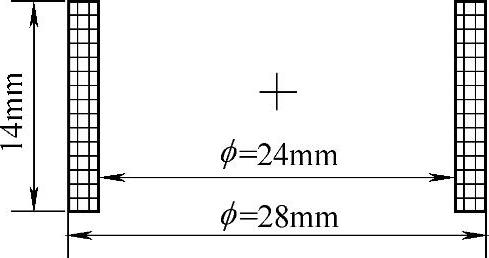
图4-72 螺线管线圈尺寸示意

设每匝线圈通以2kA的电流，利用软件Ansoft对盘状线圈上表面的磁场分布进行仿真计算，可得图4-73所示的磁场径向分量，在盘状线圈表面的大部分区域里，该径向磁感应强度分量变化不大。为简单起见，计算时取其中间位置最大值B_pan=0.55T。

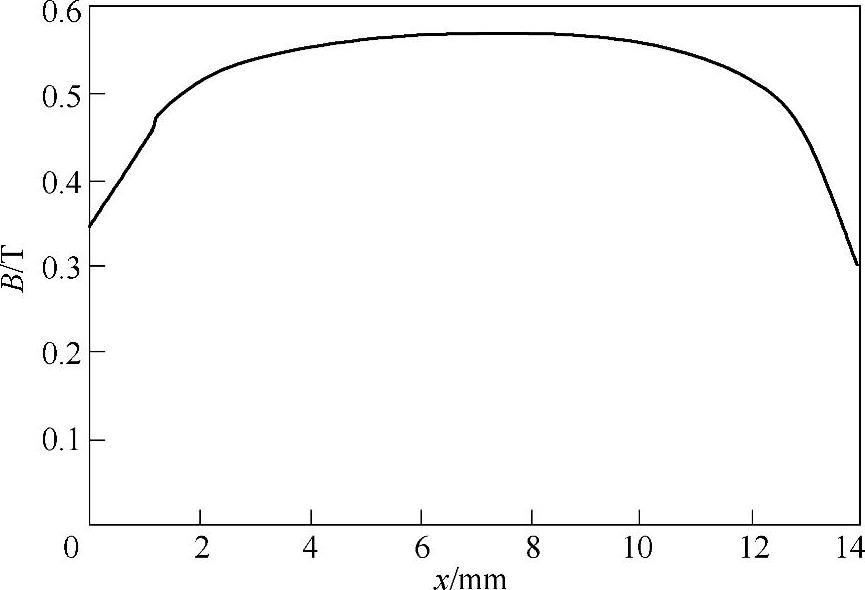
图4-73 盘状线圈上表面磁场径向分量

通过仿真也可得到螺线管线圈外表面磁场的径向分量，如图4-74所示，其在螺线管线圈外表面的大部分区域内线性度较好，近似为直线，最大值为B_lmax=0.52T。

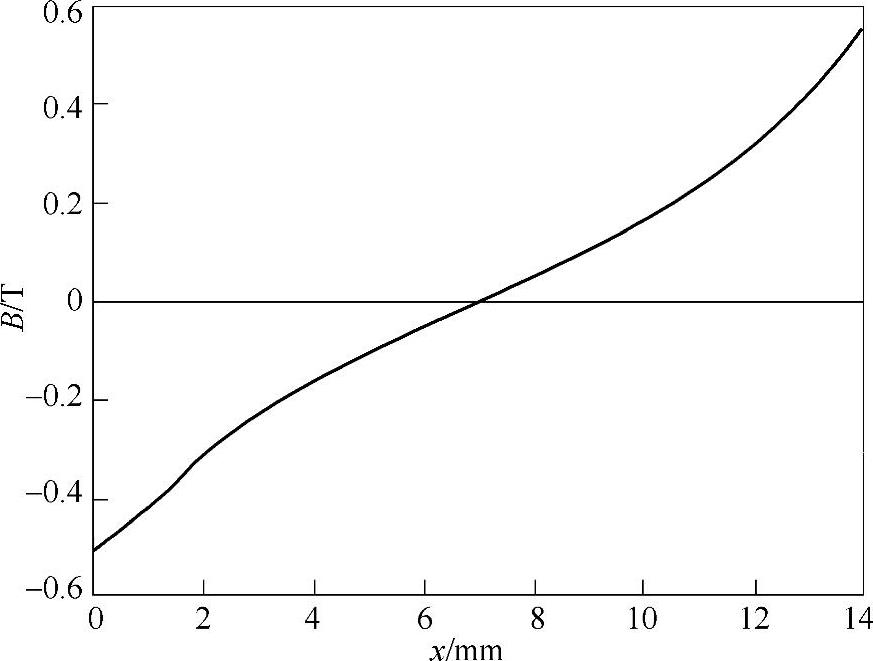
图4-74 螺线管线圈外表面磁场径向分量

分别按照4.2.1节和4.2.3节给出的电磁机构拓扑，在盘状线圈上部布置同样大小的盘状线圈，在螺线管外部嵌套一个紧贴的反绕螺线管线圈，则两个线圈受到的初始电磁力分别为

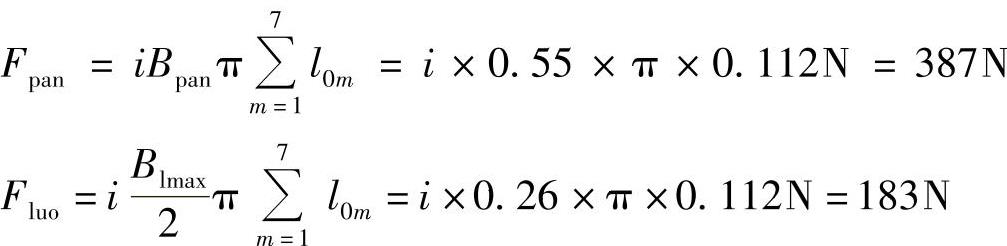
式中，F_pan为盘状可动线圈受到的电磁力，F_luo为反绕螺线管线圈受到的电磁力，i为线圈电流，l_0m为第m匝的线圈周长。

比较两式可知：F_pan/F_luo≈0.5，即反绕嵌套式电磁机构的初始电磁力约为盘状推斥型电磁机构的50%左右。但是也应看到，反绕嵌套式电磁机构在运动过程中，其电磁力始终与电流的二次方成正比，且计算简单；而线圈—线圈式电磁机构的电磁力则逐渐减小，且计算比较复杂。