前面研究的音圈电机式电磁机构，主要由永磁体、线圈和铁心构成，结构简单，可控性好，但因需要铁心和永磁体等非线性材料，当线圈中的电流很大时，会出现磁饱和和退磁等不利问题。电动机操动机构具有控制准确和动作分散性小等优点，但也存在动作时间较长、控制方法复杂以及需要特殊的稳态保持机构等问题。盘状推斥型电磁机构利用两个平板状线圈（或平板线圈与铜盘）之间产生斥力而实现驱动，其电感和时间常数小，可在极短时间内由电容放电产生很大的脉冲电磁力，具有动作速度快、时间分散性小等优点，但因动作速度太大引起的碰撞振动问题尤其突出，需要较复杂的缓冲机构，且其动作过程的可控性较差，不利于实现速度跟踪控制。

事实上，简易而可靠的物理拓扑结构，以及简单而准确的数学分析模型，对实现电磁电磁机构的快速性与可控性至关重要，也是优化结构设计和运动控制的前提基础。

不同于上述几种机构的原理，利用空心线圈具有电感和时间常数均相对较小的优点，基于两个螺线管线圈边缘电磁场的相互作用，提出了一种新型的电磁驱动机构。该机构除具有结构简易可靠的优势外，还具有数学分析模型简单而准确的优点。通过样机实验验证了该机构的有效性，为实现电磁机构的优化设计以及运动过程的可控奠定了基础。

4.2.3.1 机构原理

该新型电磁机构的基本物理拓扑如图4-40所示，它由两组线圈L₁与L₂构成。其中，可动线圈L₁是同一绕向绕制的螺线管线圈a；固定线圈L₂包含用一根导线绕制而成的大小相同、绕向相反的线圈b和c。线圈b与线圈a的顶端对齐；线圈c的顶端与线圈a的中线对齐。线圈a底端到线圈c底端的距离即为可动区间。当a、b、c三个线圈流过同一电流时，L₁在L₂产生的磁场将相互作用而发生竖直方向的相对运动（图中所示为可动线圈L₁竖直往上运动）。

这里为分析方便，以L₂在L₁产生的磁场中受力为例。L₁通过电流时将产生图4-41所示的初始磁场分布（仅画出x=0处的yz平面）。对应图4-41所示的磁场分布剖面图，在区域m、区域n内的磁场径向（水平）分量大小与方向如图4-42所示，分别以实线、虚线表示。这样，以z=0为分界面，L₁通流后在上、下两个半球区域产生的径向（水平）磁场分量方向相反，且越靠近螺线管线圈a的两个端部，径向（水平）磁场分量越大。因此，分处两个区域的反向串联的线圈b与线圈c将受到同一方向的竖直电磁力（利于快速驱动）。按照图4-40所示的电流方向，L₂将受到竖直往下的合力，亦即L₁受到向上的电磁力而产生运动。

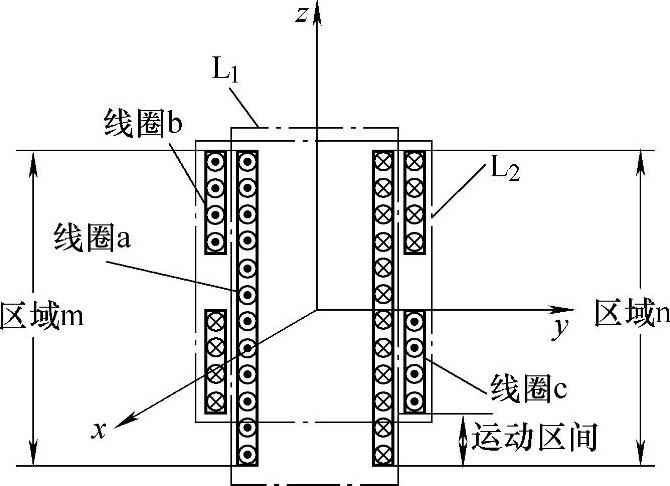
图4-40 电磁机构拓扑示意

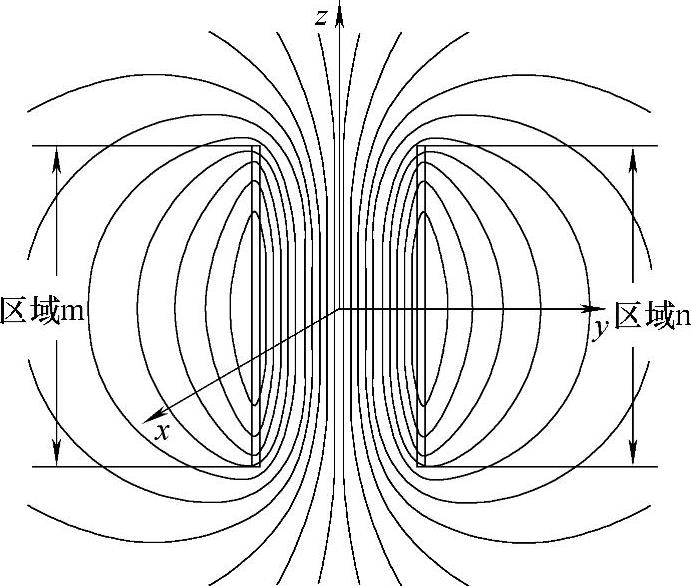
图4-41 线圈L₁产生的磁场分布

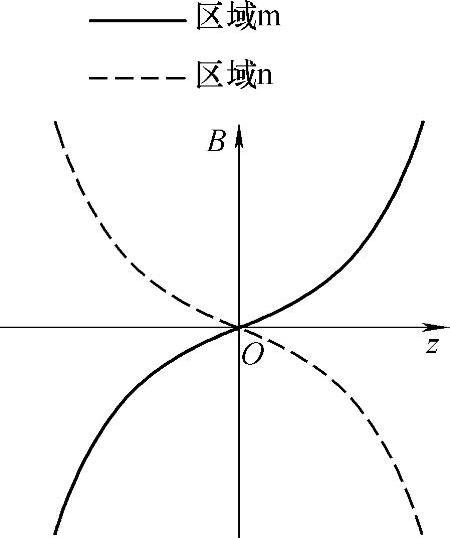
图4-42 沿z轴分布的径向（水平）磁场分量

4.2.3.2 解析基础

1.线圈L₁产生的径向磁场

为求解通流多匝线圈在空间任意一点产生的磁感应强度，首先分析单匝通流线圈的情况，建立如图4-43a所示的柱坐标系。单匝通流线圈在空间任一点产生的磁感应强度径向分量计算公式为

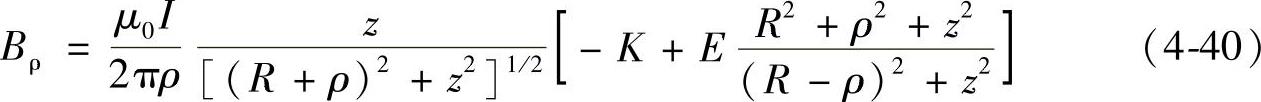
式中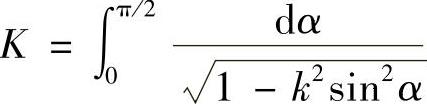，，，，K、E分别为第一类和第二类完全椭圆积分。

对于多匝密绕线圈，则可建立图4-43b所示的柱坐标系。此时式（4-40）中的电流可用电流密度J和线圈轴向微分位移dh来表示，即。对于空间任意一点由多匝密绕线圈产生的磁感应强度径向分量，由式（4-40）积分可得

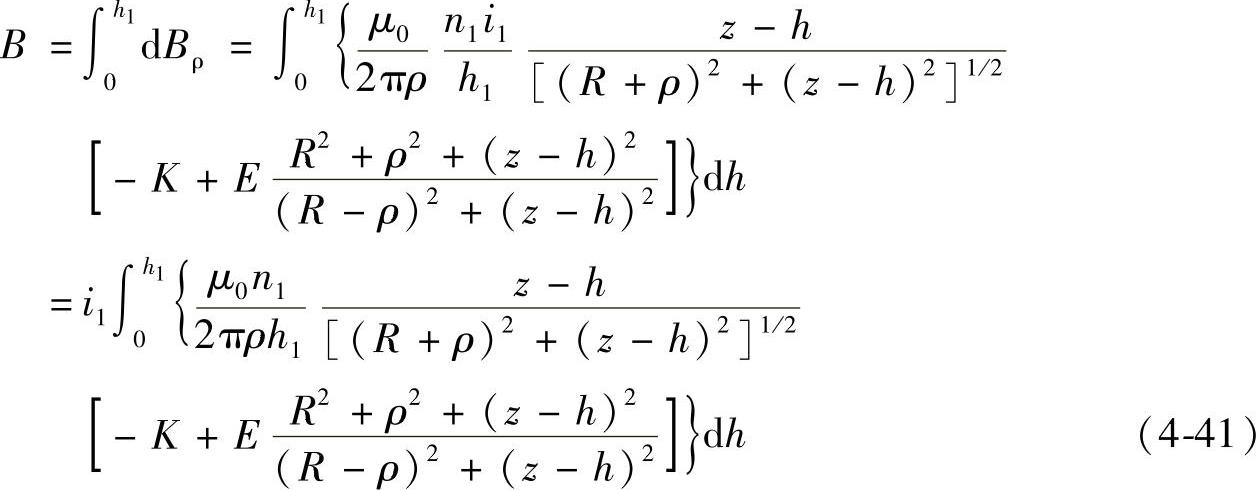
式中，i₁、n₁、h1分别为线圈L₁的电流、匝数和线圈高度。

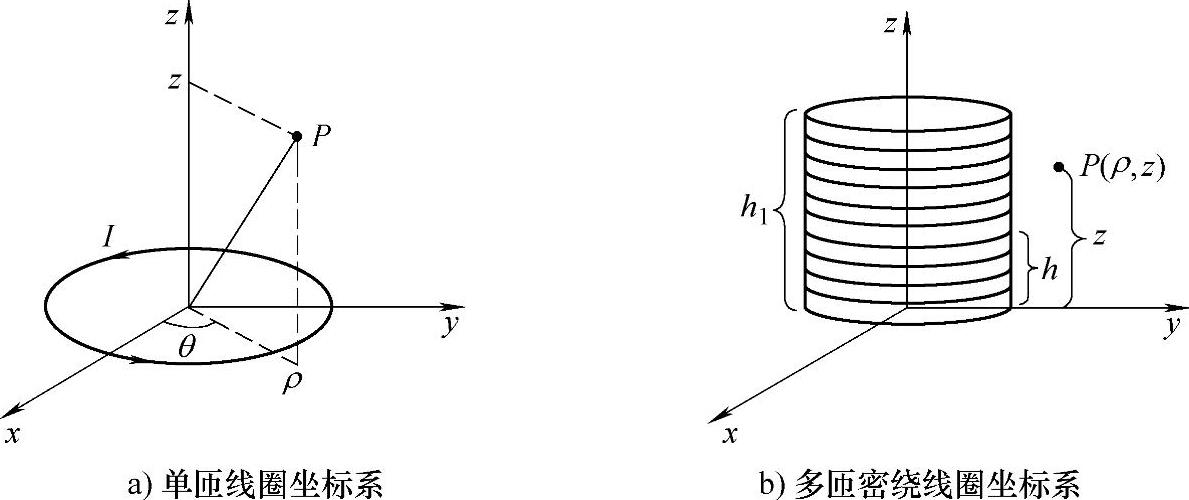
图4-43 磁场分析所用柱坐标系

由以上分析可知，磁感应强度径向分量B只与结构参数有关，即当线圈L₁的半径r₁、高度h₁给定时，任意一点P（ρ，z）处的磁感应强度径向分量B与电流i₁成正比。

式（4-41）中含有第一类和第二类完全椭圆积分，解析计算较为复杂，为进一步分析线圈L₁的径向磁场分布特性，得出更简洁的数学描述，可采用数值方法。以实际设计的样机参数为例，线圈L₁的直径为30mm，长度为96mm，并设电流i₁为1（归一化），以线圈轴线为中心，在线圈L₁长度范围内计算ρ=50mm处的径向磁场，沿线圈L₁的轴向考察三个区间的情况：①0≤z≤10mm；②38mm≤z≤58mm；③86mm≤z≤96mm。

为简化机构的分析模型，可采用一元线性回归分析，获得上述轴向区间内磁感应强度径向分量B与轴向距离z之间的简单数值关系。

设三个区间的回归函数形式均为B=a+bz。由于对称性，对于两个端部区间只考察0≤z≤10mm区间即可。

（1）0≤z≤10mm区间

a₀=-3.704×10^-5，b₀=1.2024×10^-3，相关系数γ₀=0.98729，即

B=-3.704×10^-5+1.2024×10^-3z（0≤z≤0.01） （4-42）

（2）38mm≤z≤58mm区间

a₁=-1.3058×10^-5，b₁=2.7175×10^-4，相关系数γ₁=0.99984，即

B=-1.3058×10^-5+2.7175×10^-4z（0.038≤z≤0.058） （4-43）

由式（4-42）、式（4-43）及相关系数表明，在线圈L₁的轴向长度范围内，两个端部及中间区域的B与z线性相关度很高，可近似认为其与轴向距离z成线性关系。

2.运动过程中穿过线圈L₂的总径向磁场

该机构的精确分析涉及电磁耦合、机械运动等问题，是一个变参数的非线性系统，一般需进行复杂的电磁场计算。但根据4.2.3.2节“1.线圈L₁产生的径向磁场”的分析，线圈L₁产生的磁场径向分量具有对称性（关于z=h₁/2对称，但符号相反），且在两个端部及中间区域的径向磁场分布可线性化处理，这使得分析大为简化。如图4-44所示，点划线框代表组成线圈L₂的两个反向串联的线圈b与c所处位置，其初始位置分别位于图4-40所示线圈L₁的上端部和中线。

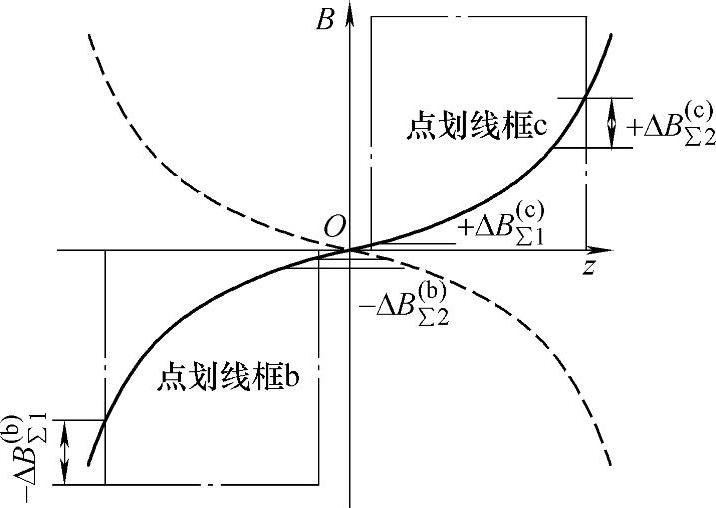
图4-44 运动时垂直穿过线圈L₂的径向磁场变化

考虑到组成L₂的两个线圈b、c的绕向相反，对式（4-41）积分可得到穿过线圈L₂的磁场径向分量总和为

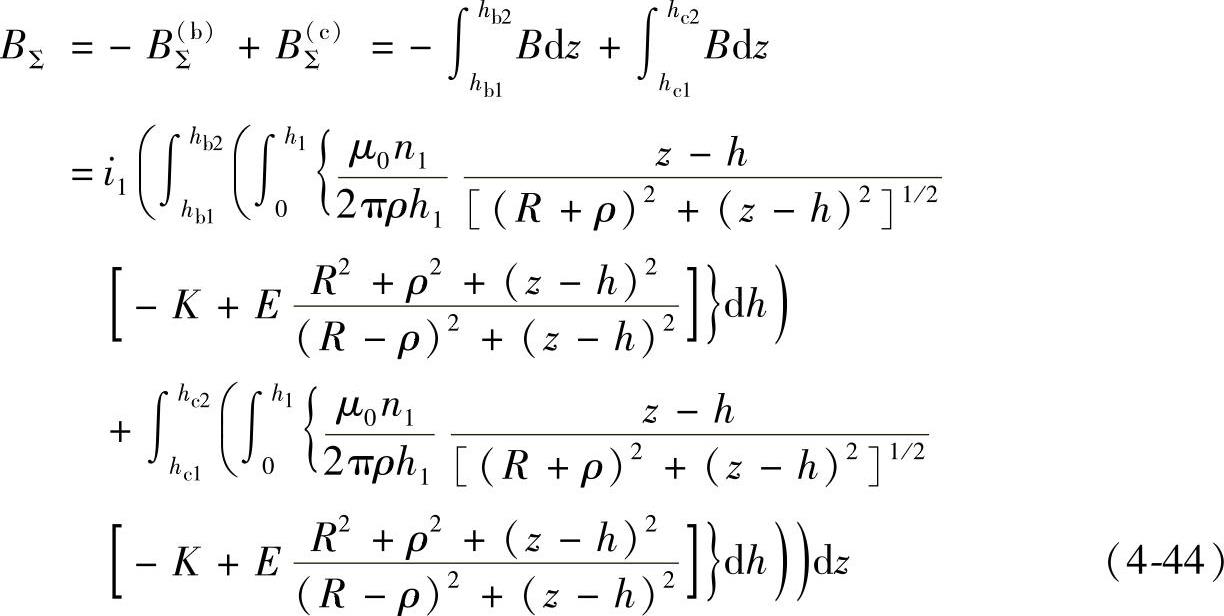
式中，BΣ表示穿过线圈L₂的磁场径向分量总和；上标（b）、（c）分别对应于组成L₂的线圈b和c；h_b1、h_b2与h_c1、h_c2分别为线圈b、c的上下两端部的坐标值；i₁为线圈L₁的电流；n₁、h₁、K、E、k²的意义同式（4-41）。

运动时，穿过线圈b、c的磁场径向分量的总变化量分别为

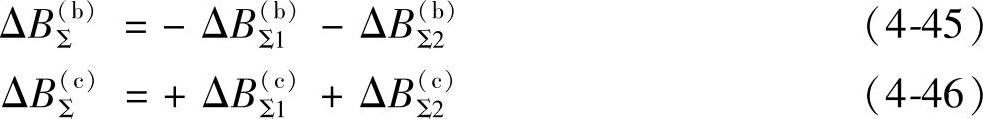
这里，下标1、2则表示线圈b或c的上、下两端部。

鉴于磁场分布的对称性，以及对螺线管两个端部及中间区域磁场的线性化处理，则有如下关系：

因此，可得运动时穿过L₂的磁场径向分量总变化量为ΔBΣ，即

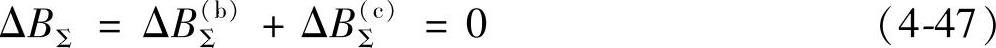
式（4-47）表明，由线圈L₁单位电流产生的垂直穿过线圈L₂的磁场径向分量总和BΣ，在运动过程中近似保持恒定，即式（4-44）中等号右边除去电流i₁外的定积分为常数，可记为C_e。因此式（4-44）可改写为

BΣ=i₁C_e （4-48）

3.等效分析模型

根据能量守恒，系统向可动线圈输入的能量，即电磁力F（t）所做的功，转化为可动线圈的动能1mv²2和克服摩擦力f（t）等所做的消耗功。可动线圈L₁的受力分析如图4-45所示。

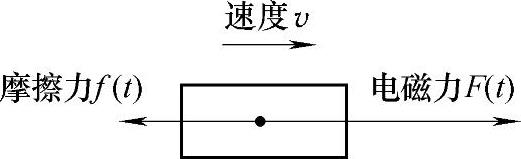
图4-45 可动线圈L₁受力分析

由图4-45可知，ma=F（t）-f（t），其中m为可动线圈的等效质量。则速度为

当线圈密绕时，L₂（包括线圈b和c）所受电磁力可用下式表示为

式中，i₂、n₂、h2、l2分别为L₂的电流、匝数、长度以及每匝线圈的周长；B、BΣ的意义分别与式（4-41）、式（4-48）相同。

将式（4-48）代入式（4-50），可得

由于线圈L₁和L₂通入同一电流，即i₁=i₂=i，则

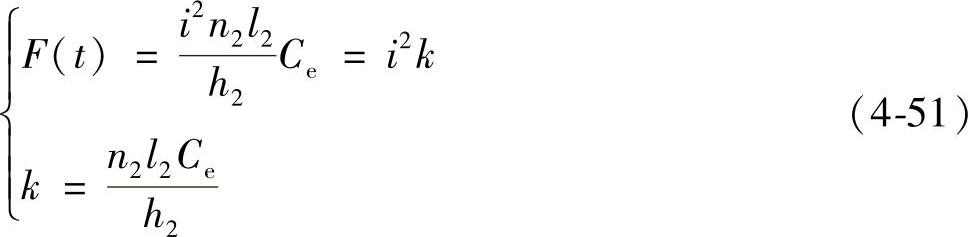
k是一个只与机构拓扑结构有关的常数，为此，将其定义为线圈L₁和L₂的空间相互作用系数。若线圈的运动速度为v，则电磁功率为

p（t）=i²kv （4-52）

空间相互作用系数的定义表明，针对该种机构，其运动过程的电磁力与电流的二次方成正比，即线圈L₁和L₂之间的耦合关系可用一个常数来简单表示，而其值可根据机构的几何拓扑经计算事先得到，这大大简化了由电磁场来计算复杂电磁耦合关系的过程，为机构参数的优化、机构控制器的设计以及运动过程的实时控制提供了理论基础。

将式（4-52）的表达式与一般电阻功率表达式对比可知，机构的运动特性可用一个等效电阻来表示，即

R′=kv （4-53）

该机构的运动行程与螺线管长度相比一般较短，如实验样机，其行程（5.5mm）只占线圈总长度（96mm）的5.7%；再者，该机构中线圈b、c与线圈a的空间布置属于差动结构，因此，L₁与L₂之间的总电感L在整个运动过程中变化不大，实测结果也证实了这一点。后文计算时取最大电感和最小电感的平均值。

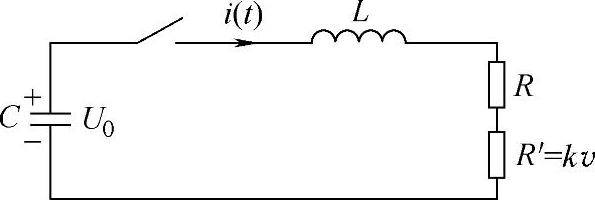
图4-46 机构运动的等效分析电路

由于该机构的动态模型可简化为一个与速度大小成正比的电阻R′=kv，因此，当由电容放电回路来提供机构的驱动电流时，其过程可用一个R-L-C放电回路来描述，如图4-46所示。其中，R、L、C分别表示放电回路电阻、电感及电容，i（t）为回路的放电电流，U₀为放电电容的初始电压。

令RΣ=R+R′=R+kv，并根据u_L=L di/dt，由图4-46可得回路微分方程为(www.daowen.com)

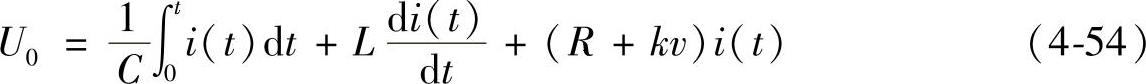
式中，速度v由式（4-49）确定。计算时，对式（4-49）和式（4-54）进行离散化，可得到数值方程组（4-55），由此可求解该电磁机构的运动特性。

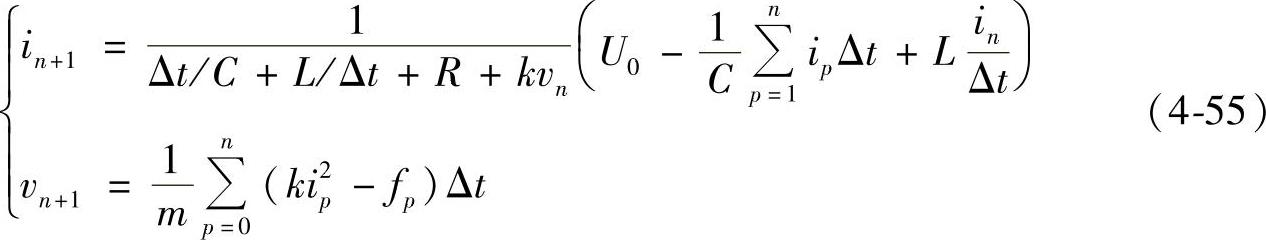
4.2.3.3 数值仿真与样机实验

根据前文建立的电磁机构数学模型，针对具体设计的实验样机进行仿真计算。具体机构参数如下：

线圈a（组成线圈L₁）的直径为30mm，长度为96.2mm；线圈b、c（组成线圈L₂）的直径为50mm，长度均为37mm；线圈及回路总电感的最大、最小、平均值分别为20.7μH、19.7μH、20.2μH；回路总电阻为0.16Ω，放电电容为190μF；可动线圈的等效质量为280g；运动行程为5.5cm；实验测得摩擦力约为1.1N。

1.仿真结果

根据式（4-51）可求得机构的空间相互作用系数k=5.192×10^-5，测得回路电感平均值为20.2μH。将机构的其他相关参数代入方程组（4-55），可得到如下仿真计算结果：U₀=3000V时，完成5.5mm行程约需要5.75ms，其电流、运动速度和行程波形分别如图4-47～图4-49所示；U₀=4000V时，完成5.5mm行程约需要3.28ms，其电流、运动速度和行程波形分别如图4-50～图4-52所示。

图4-47 电容电压3000V时的驱动电流

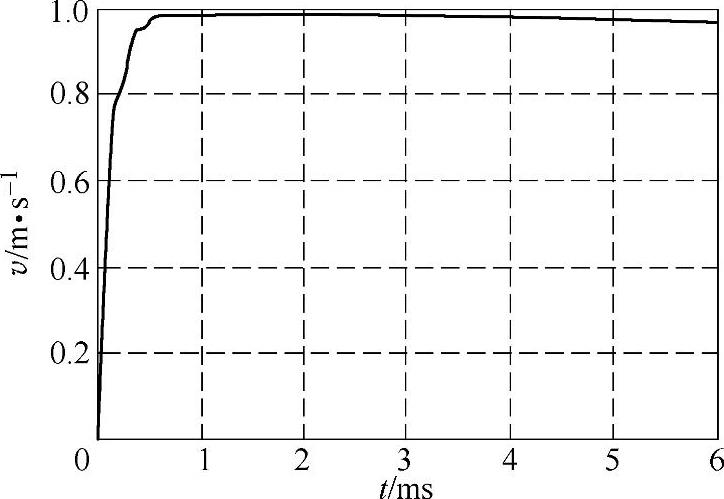
图4-48 电容电压3000V时的运动速度

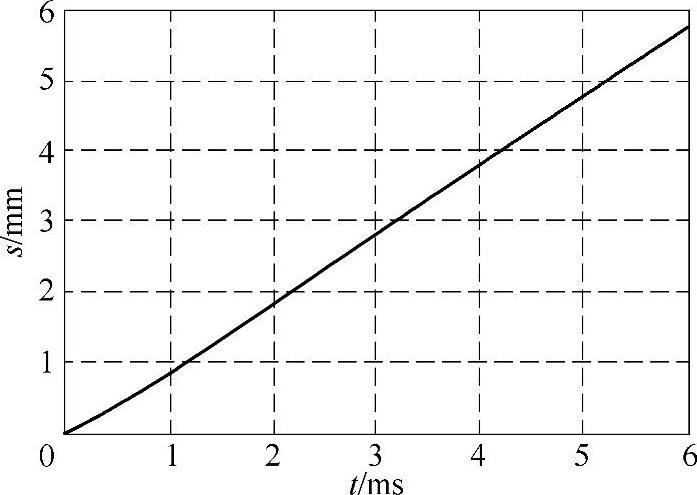
图4-49 电容电压3000V时的行程变化

图4-50 电容电压4000V时的驱动电流

图4-51 电容电压4000V时的运动速度

图4-52 电容电压4000V时的行程变化

图4-53 新型电磁机构的实验样机

2.实验结果

设计的样机实物和实验测试平台如图4-53和图4-54所示，实验时测取电流波形和完成5.5mm行程所需的时间。主回路由充电电容、真空断路器、反绕嵌套螺线管式电磁机构、分流器组成。电压由电容式分压器进行测量；电流测量由分流器完成；而行程时间T，则采用YD-81振动传感器测量机构的起始碰撞时刻来间接确定。

U₀=3000V时，完成5.5mm行程约需要5.82ms，其放电电流（标识2）和振动信号波形（标识3）如图4-55所示；U₀=4000V时，完成5.5mm行程约需要3.34ms，其放电电流（标识2）和振动信号波形（标识3）如图4-56所示。

图4-54 新型电磁机构的测试平台

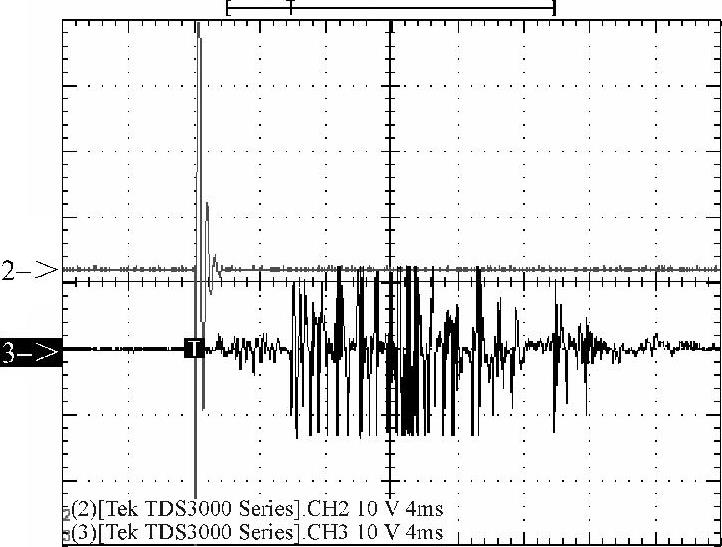
图4-55 电容电压3000V时的放电 电流及振动信号

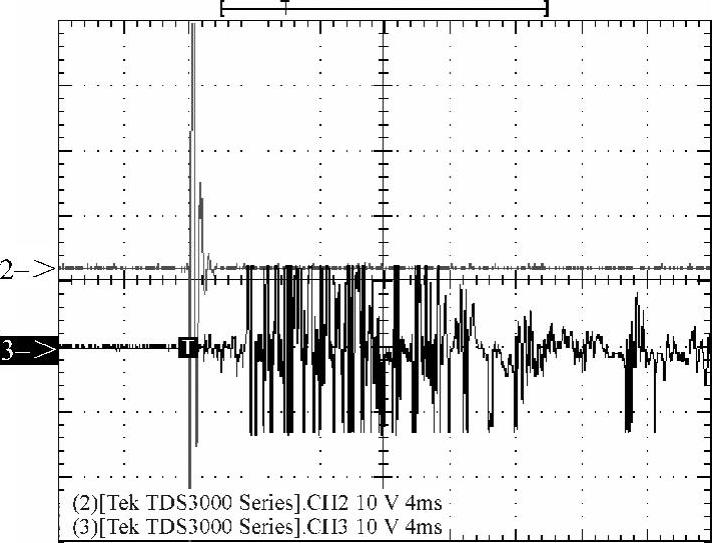
图4-56 电容电压4000V时的放电 电流及振动信号

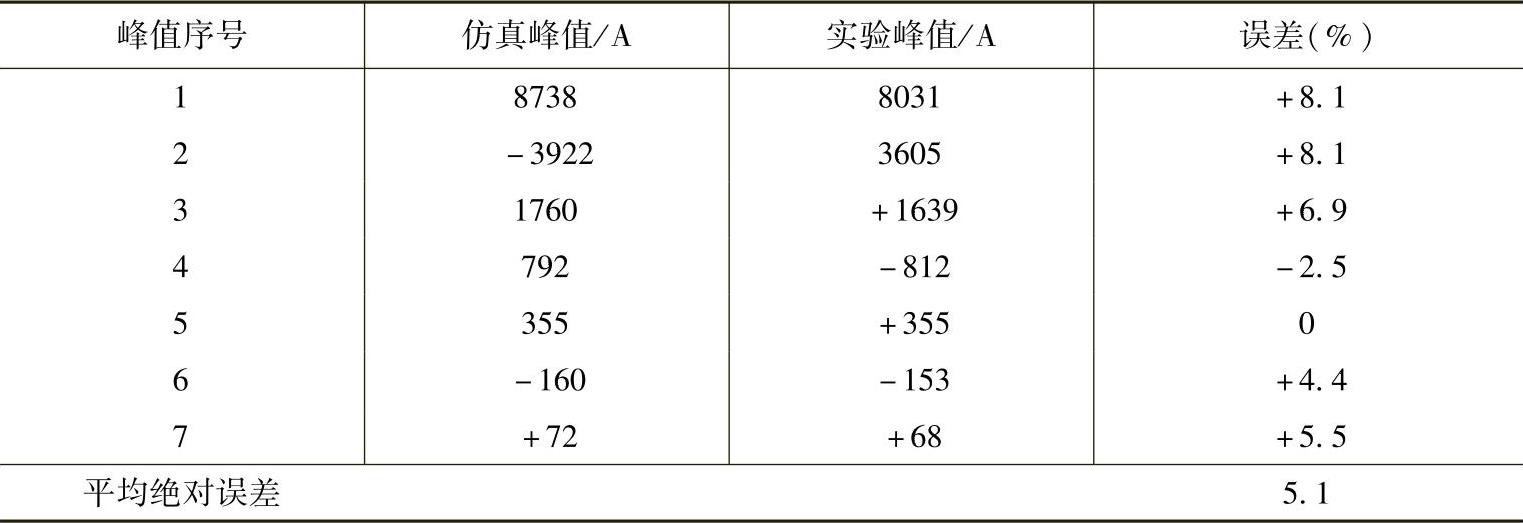
仿真与实验结果的对比见表4-8～表4-10，放电电流峰值的最大相对误差在10%左右，运动时间的相对误差在2%以内。表4-9和表4-10中的数据，是从放电起始算起的共7个波峰和波谷值的对比。究其误差来源，主要来自于简化模型本身的误差、实验测量误差以及机构运动过程中摩擦力引入的误差等。但这些误差很小，仿真与实验结果能够较好地吻合，表明所建立的结构数学模型是正确有效的。

表4-8 行程时间对比

表4-9 电容电压3000V时的电流峰值对比

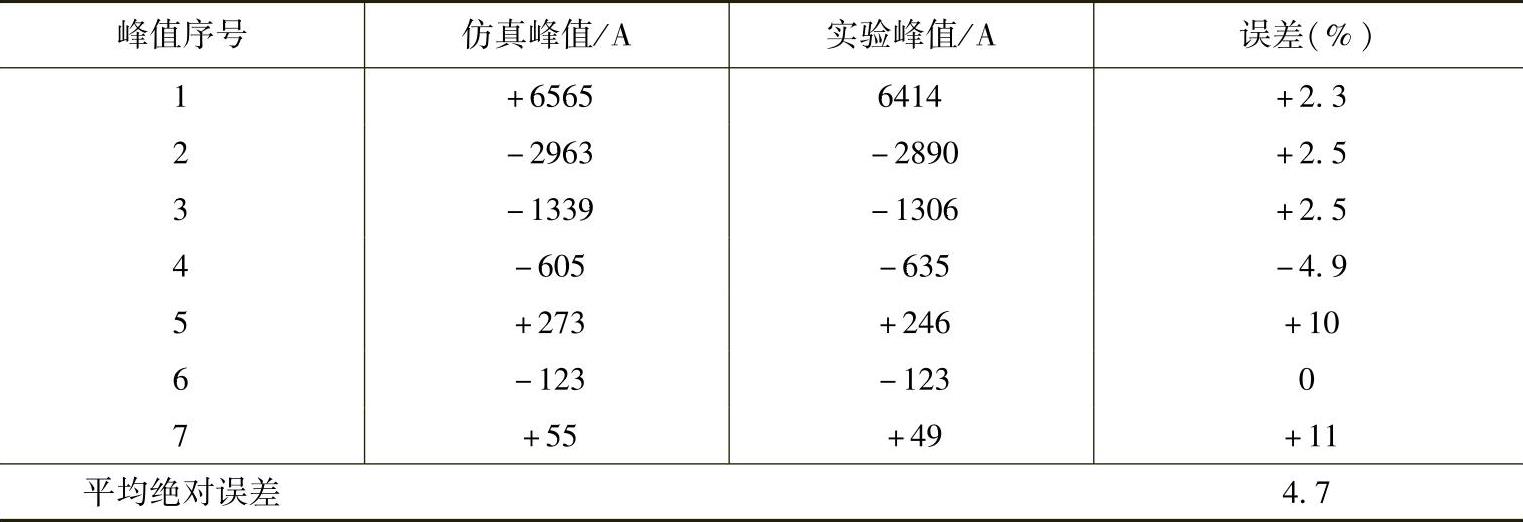
表4-10 电容电压4000V时的电流峰值对比

4.2.3.4 速度跟踪控制策略及仿真分析

若将可动线圈L₁和固定线圈L₂串联放电，则由式（4-51）可知，在运动过程中电磁力将一直保持正值，使机构始终处于加速状态，而无法进行减速。欲实现运动速度的跟踪控制，必须将可动线圈L₁和固定线圈L₂分别接入两个放电回路，以产生反向电流并形成减速电磁力。系统运动方程可由式（4-56）描述。

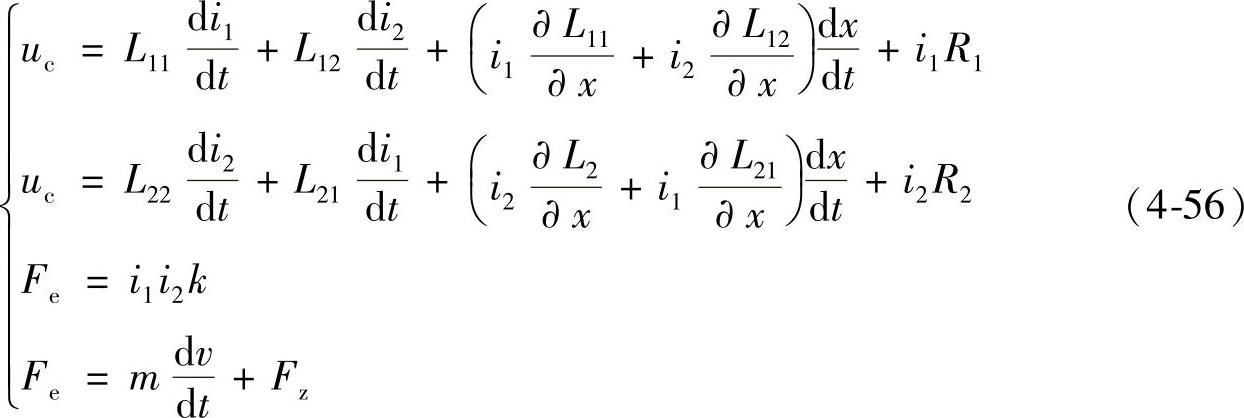
式中，u_c为电容电压；i₁、R₁、L₁₁分别为可动线圈回路的电流、电阻、自感；i₂、R2、L22分别为固定线圈回路的电流、电阻、自感；L₁₂、L₂₁分别为可动线圈与固定线圈的互感，L₁₂=L₂₁；k为相互作用系数；F_e为电磁力；F_z为反力；x、v分别为行程和速度。

根据前文对该机构拓扑的分析，L₁₂=L₂₁≈0，=0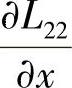，=0；同时，由前述的分析，易证明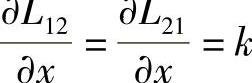。因此，式（4-56）可简化为

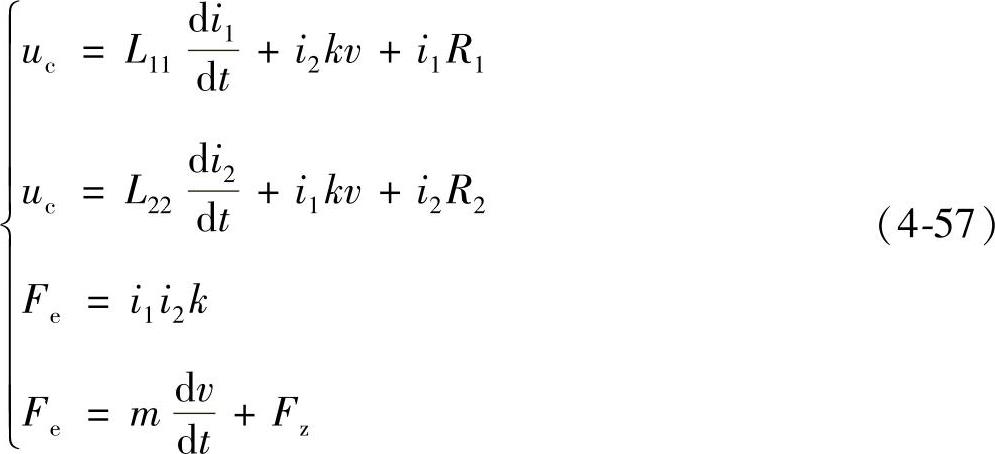
式（4-57）即为描述该型电磁机构的动态方程组，据此可搭建其动态运动过程的仿真模型，其中两个放电回路的耦合作用可分别用两个可控电压源等效，固定线圈回路对可动线圈回路的耦合作用可等效为电压源u_control12=i₂kv，可动线圈回路对固定线圈回路的耦合作用可等效为电压源u_control21=i₁kv。

由于涉及两个放电回路，则实现速度跟踪控制的主回路方案可有三种：①L₁和L₂分别接入两个单相H桥式主回路，由各自的放电电容进行放电；②其中一个接入单相H桥式主回路，另外一个接入自由放电回路，分别由各自的放电电容进行放电；③L₁和L₂所在主回路使用同一个放电电容，其中一个回路为单相H桥式主回路，另外一个为自由放电回路。

图4-57 速度跟踪控制主回路原理图

为降低控制复杂性并减少主回路器件数量，选用第三种控制方案，如图4-57所示。图中，L₁为可动线圈，R₁为L₁的回路电阻；L₂为固定线圈，R₂为L₂的回路电阻；C为放电电容。

根据前文的理论分析与建模方法，基于PSIM构建了该型电磁机构分闸运动特性的控制仿真系统，如图4-58所示。

图4-58 反绕嵌套螺线管式电磁机构的动态特性仿真系统

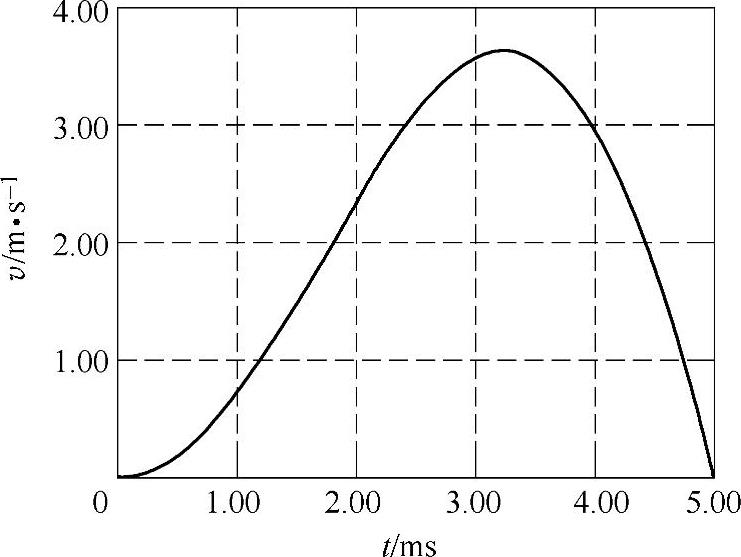
图4-59 给定的分闸运动速度曲线

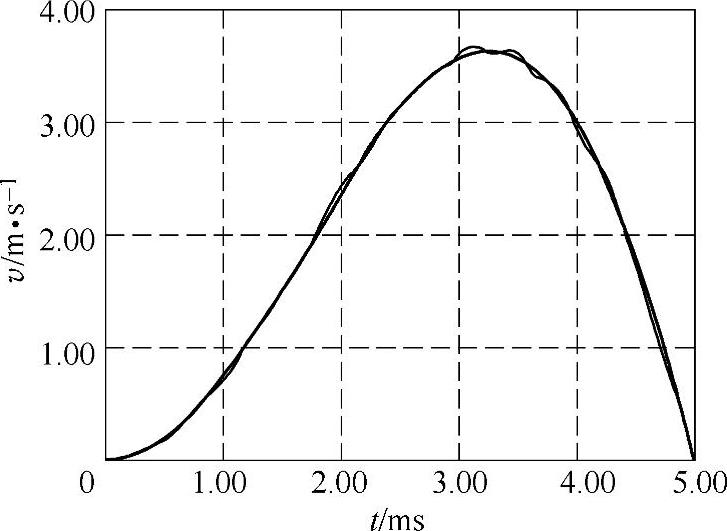
图4-60 给定与实际运动速度曲线的比较（波动曲线为实际运动曲线）

设给定的真空开关分闸运动最优速度曲线如图4-59所示，以此作为电磁机构的速度跟踪控制目标。仿真时参数设计为：运动部分质量m=1kg，运动行程为10mm；放电电容C为10000μF，充电电压为800V；L₁直径为5.2cm，长度为8cm，线圈匝数为80，其回路电感为210mH，电阻为0.11Ω；组成L₂的两个反绕线圈直径为4.4cm，单个长度为3cm，单个线圈匝数为30，其回路总电感为100mH，电阻为0.07Ω。

以图4-59所给定的速度曲线作为参考目标，利用图4-58构建的仿真系统，对电磁机构的动作特性进行仿真分析，结果如图4-60～图4-63所示。

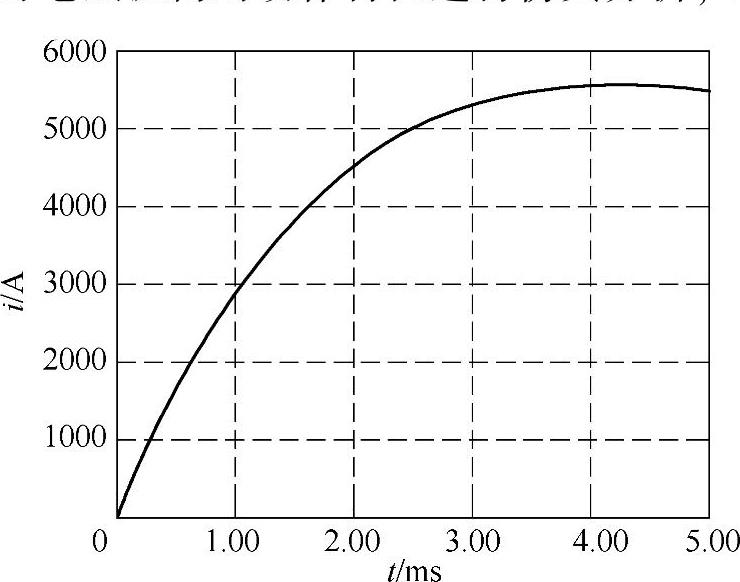
图4-61 线圈L₁回路放电电流曲线

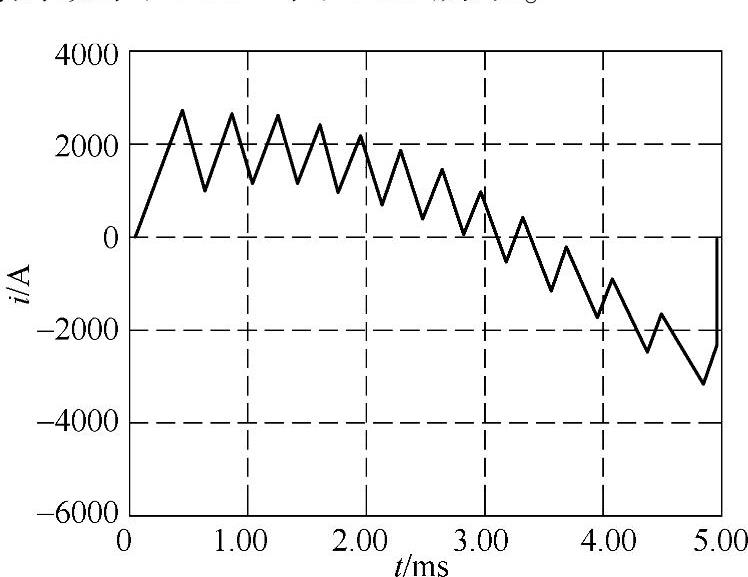
图4-62 线圈L₂回路受控放电电流曲线

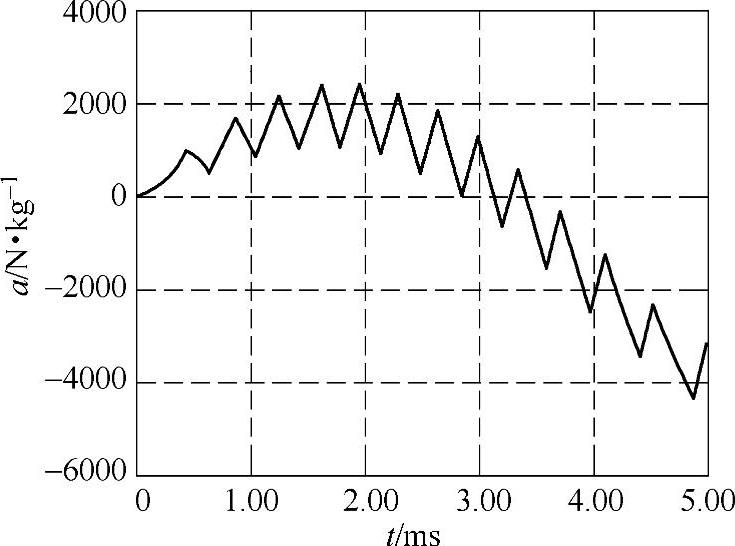
图4-63 机构运动加速度曲线

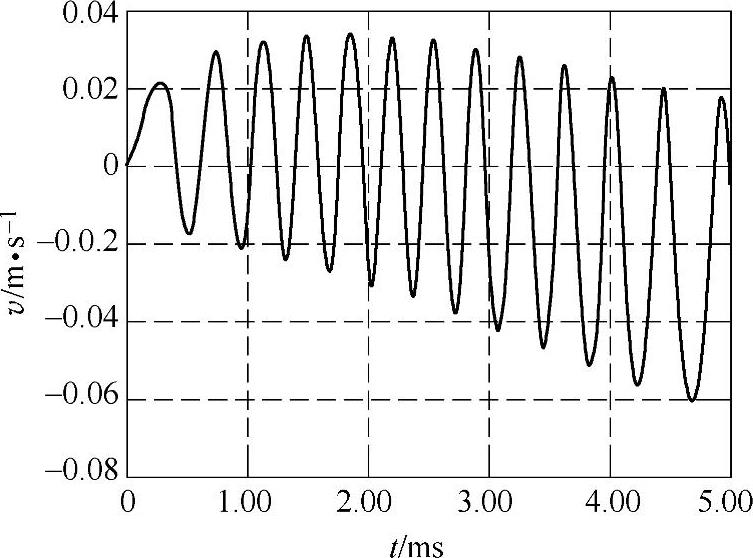
图4-64 机构运动速度跟踪控制的误差曲线

由仿真结果可知，为提高机构的动作快速性，需提供较大的脉冲电磁力；同时，为实现速度的最优跟踪控制，亦需在运动过程中通过控制L₁线圈的主回路将该回路电流反向，以提供机械缓冲所需的较大脉冲电磁力。

机构运动结束时线圈内仍有较大的剩余电流，倘不采取有效措施释放电感能量，则会造成触头在反向电磁力的作用下产生更大反弹，甚至可能导致分闸失败。因此，临近运动结束时，提前控制线圈放电回路导通，以快速释放能量使电流到零，并充分利用双稳弹簧在半行程后变阻力为驱动力的特点，可解决该极短过程的电磁缓冲问题，具体可参见图4-62和图4-63所示曲线的末端。仿真结果还表明，倘采取4.2.2节中所述策略，在4.9ms时触发串联有400Ω电阻的放电旁路导通，则行程结束时动触头的运动速度可以控制到很小值，小于0.1m/s。此时触头的残余动能较小，约为0.025J，几乎不会发生碰撞。整个过程中速度跟踪控制的效果较好，速度跟踪最大误差约为0.06m/s，如图4-64所示。

4.2.3.5 小结

基于螺线管线圈边缘电磁场的相互作用，提出了一种新型电磁机构的空间拓扑，并研制了实验样机。针对该电磁机构的磁场分布情况，证明可利用安培力公式来简化电磁力的计算过程，大大简化了数学分析模型；提出空间相互作用系数的定义，来描述可动线圈L₁和固定线圈L₂之间的耦合关系，为该电磁机构的优化设计和运动过程的实时控制奠定了理论基础。

仿真计算与样机实验结果符合较好，表明所建数学分析模型的有效性。