首先从满足机构的快速性入手，研究适合这一要求的拓扑设计。体积相同的空心线圈要比有铁心线圈的电感小得多，这将大大缩短机构线圈的励磁时间。下面将针对一种盘状推斥型快速电磁机构拓扑，通过合理设计实现两个线圈之间电磁力的最优化。通过建立其动态数学模型，研究其参数变化规律，进行机构参数优化，以使得机构在提高运动速度方面达到较佳效果。

4.2.1.1 拓扑结构及原理

所研究的盘状推斥型快速电磁机构在拓扑上有两种形式：一是由可动铜盘与两个固定的分、合闸线圈组成，称为铜盘—线圈结构；二是一个可动线圈与两个固定分、合闸线圈组成，称为线圈—线圈结构，如图4-9所示。该型电磁推力机构的一般工作原理为：通过预充电的电容器向合闸或分闸线圈放电，产生持续几毫秒的脉冲电流，与开关操作连杆固定在一起的铜盘因感应涡流而受到脉冲电磁推力作用，从而带动连杆运动，实现开关的快速关合或分断。下面以盘状铜盘—线圈结构作为主要研究对象，对其动态过程以及机构参数的优化问题进行分析。

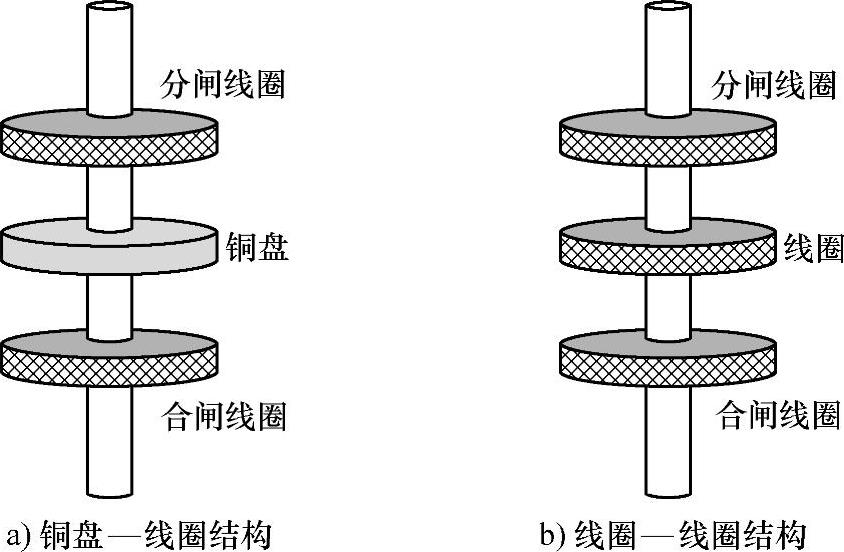
图4-9 快速电磁推力机构空间拓扑

4.2.1.2 计算方法

电磁推力机构的运动过程涉及放电回路、电磁感应耦合、连杆机械运动等多个相互作用的动态子过程，需要联合电路方程、空间磁场与涡流方程以及机械运动方程来求解其严格的动态特性。目前，对于磁场及涡流计算，多采用有限元法分析，但这种方法应用起来相当复杂，不便于实现电磁推力机构的工程优化设计。这里以铜盘—线圈结构为例，提出一种计算方法以实现各拓扑参数的优化设计。

1.两个单匝线圈之间的电磁力计算

无论是铜盘—线圈结构还是线圈—线圈结构，线圈一般做成盘型多匝，各匝的半径各不相同，而铜盘中感应的涡流也可等效为多个半径不同的同轴圆线匝。因此，描述通电线圈与铜盘之间电磁作用的基本单元，可等效为任意两个同轴的单匝线圈。为此，采用单匝双线圈模型来研究电磁作用的一般特性，如图4-10所示。

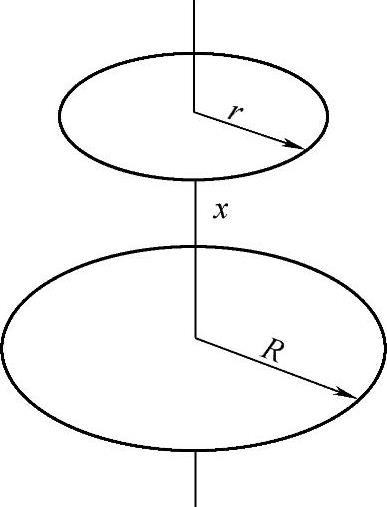
图4-10 两个单匝线圈示意图

图4-10中，上线圈为感应线圈（铜盘等效线圈）的一匝，下线圈代表通电线圈的一匝，半径分别为r和R，间距（位移）为x。根据通用的电磁计算方法可得到两个单匝线圈之间的互感M为

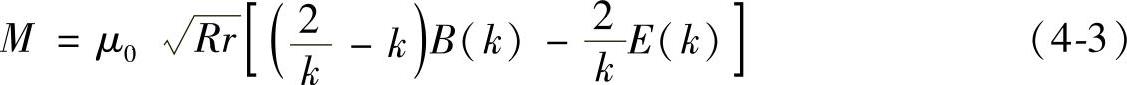
式中，

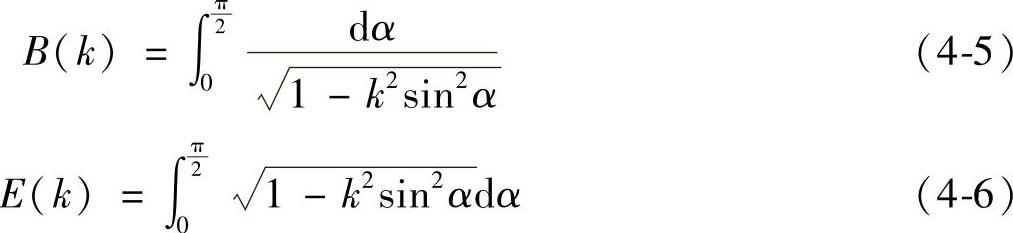
经推导可得到双线圈之间互感对位移x导数的基本公式为

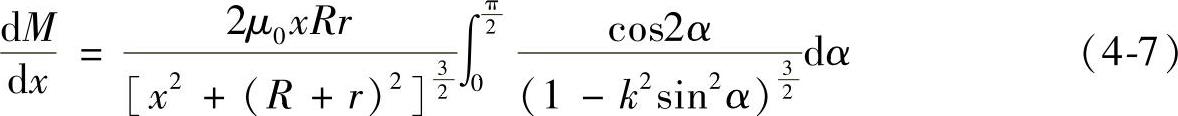
设通电线圈和感应线圈内的电流分别为i₀与i₁，则双线匝之间的电磁力F可以写成

2.铜盘—线圈间电磁力计算方法

首先分析通电线圈的电阻、自感和互感。设盘型线圈共绕N₀匝铜线（电阻率为ρ），铜线截面积为2a₀d₀（2a₀为宽度，d₀为厚度），每匝半径为r_0m，则第m匝线圈的电阻为

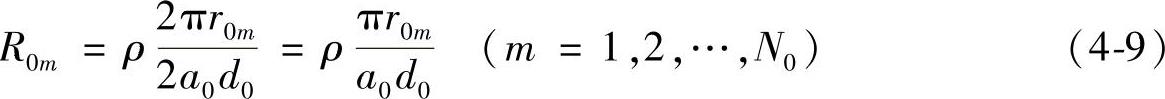
第m匝线圈的自感（包括内感与外感）为

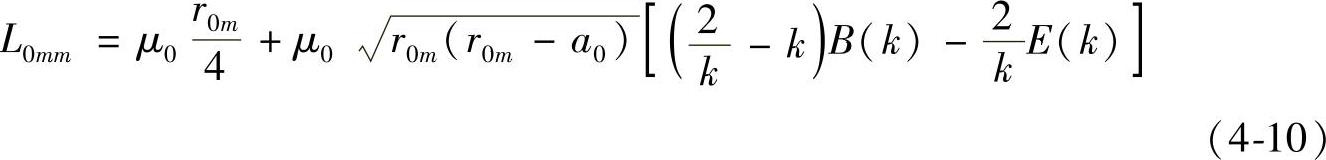
式中，。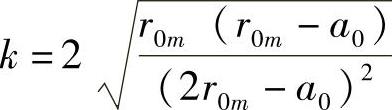

m、n两匝线圈之间的互感为

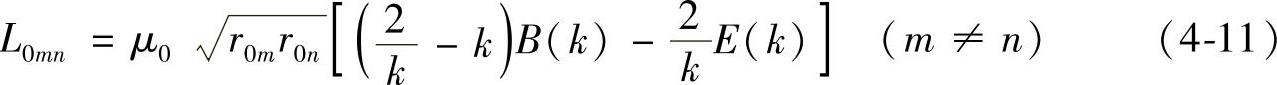
式中，。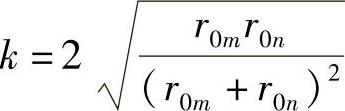

然后分析铜盘参数。将铜盘沿半径r₁等效为N₁个截面积为2a₁d₁（2a₁为宽度，d₁为厚度）的圆环，则第p个圆环的半径和电阻分别为

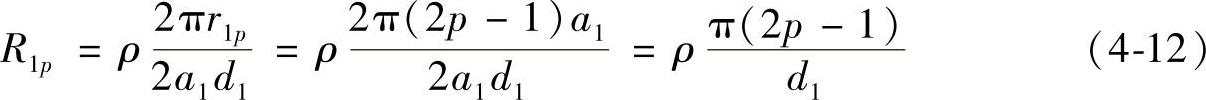
式中，r_1p=（2p-1）a（p=1，2，…，N₁），a₁=r₁/（2N₁）。

第p个圆环的自感（包括内感与外感）为

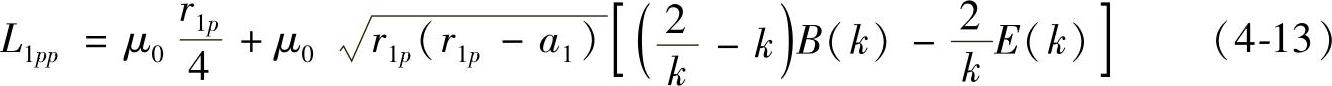
式中，。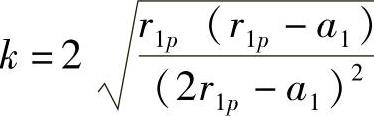

第p、q两个圆环之间的互感为

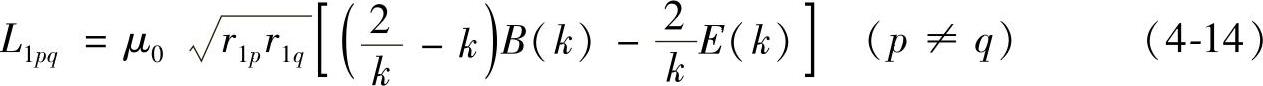
式中，。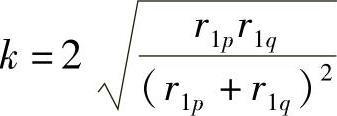

通电线圈第m匝与铜盘第q圆环之间的互感为

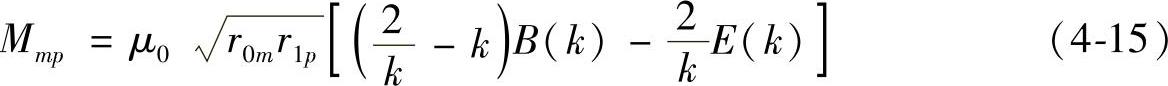
式中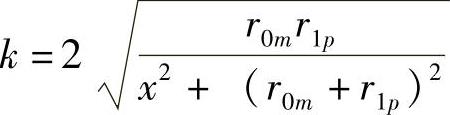，，x为铜盘相对于线圈的位移。

根据以上理论分析，可求得机构的电路方程。设通电线圈的电流为i₀，铜盘各个等效圆环中感应的涡流为i_1p（p=1，2，…，N₁），E₀为电容C充电电压初值，则可写出如下方程组：

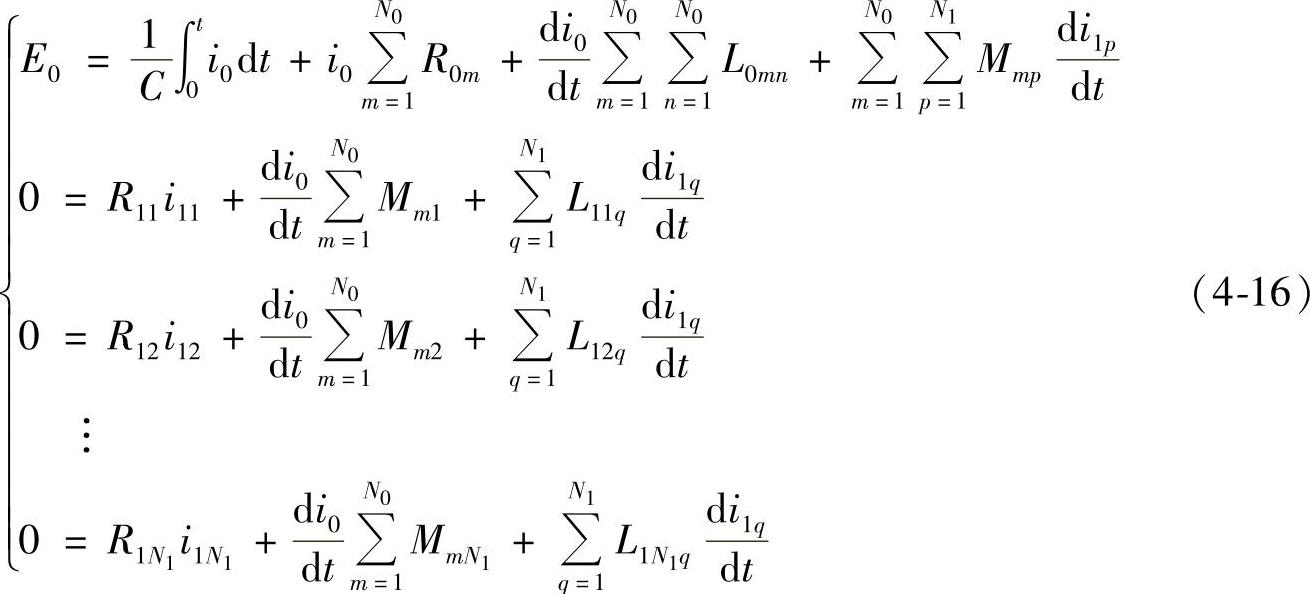
经推导，方程组（4-16）可以化为式（4-17）所示的矩阵形式：

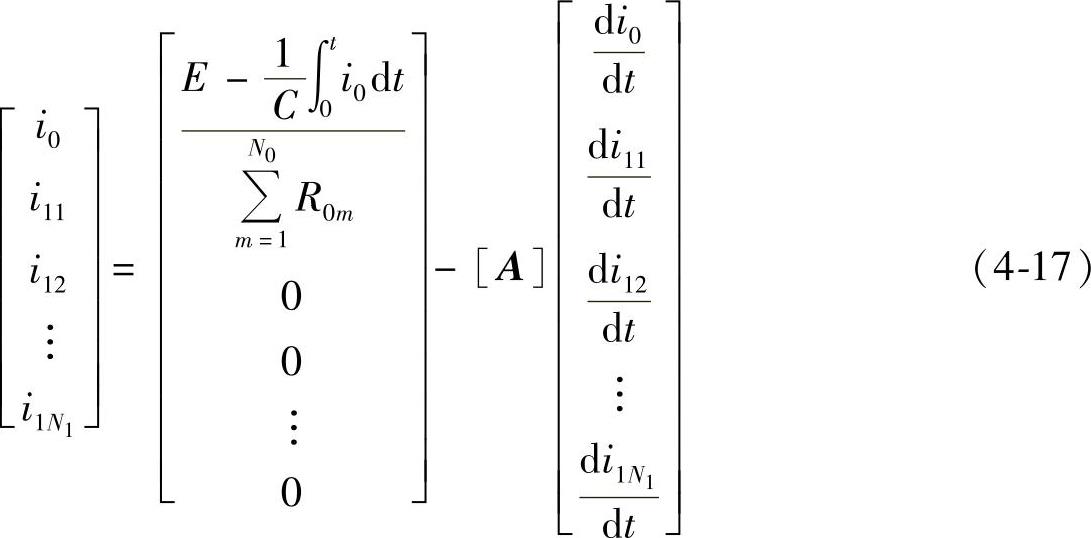
式中，A为N₁+1维的电感系数矩阵，由各个环节的自感、互感和电阻决定。将式（4-17）改写成矩阵向量形式为

考虑到数值计算的精度和收敛性问题，对式（4-19）中的电流微分方程组采用隐式离散算法（矩阵形式），其中Δt为计算步长：

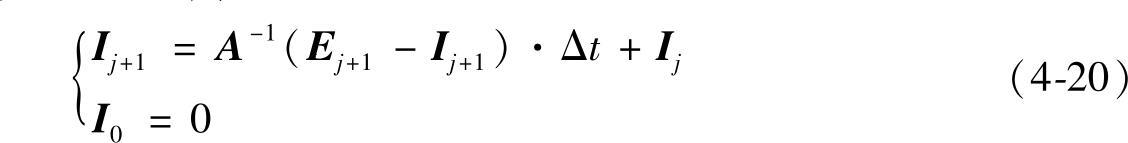
计算出各个电流后，则可利用式（4-21）计算电磁推力：

式中，。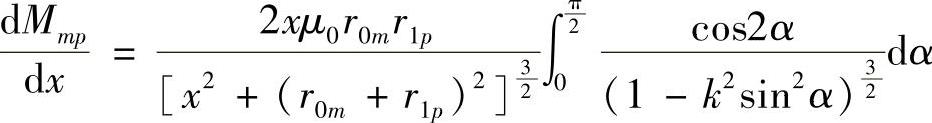

设m为铜盘和连杆系统的总质量，f（x）为运动中受到的阻力，包括弹簧力、重力、摩擦力等，则可写出如下的运动方程：

将式（4-20）、式（4-21）和式（4-22）联立，可得

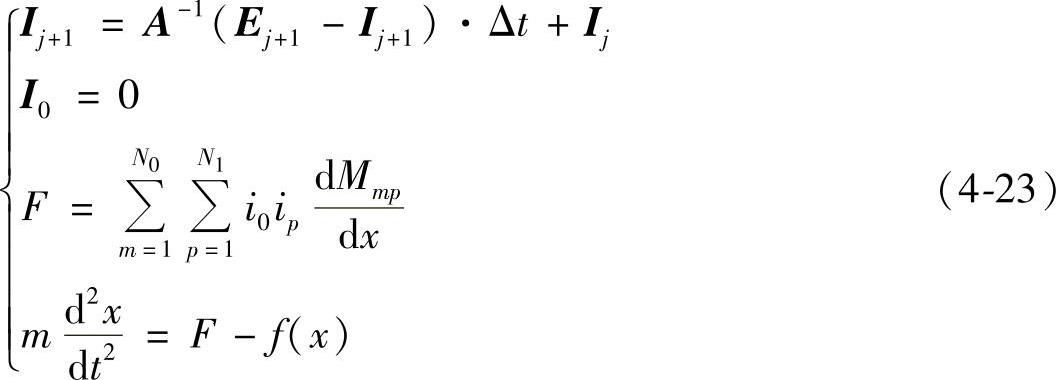
式中，N₀为通电线圈的匝数；N₁为铜盘涡流的等效匝数；M_mp为每匝线圈与每匝铜盘等效圆环之间的互感；F为总的电磁力；x为动触头的行程；m为铜盘和连杆系统的总质量；f（x）为运动中受到的阻力，包括弹簧力、重力、摩擦力等；A为N₁+1维的电感系数矩阵，由各个环节的自感、互感和电阻决定；i₀为通电线圈的电流，i₁、i₂…、i_N1为铜盘的各匝等效涡流，共同构成N₁+1阶的电流列向量I；E为N₁+1阶的电压列向量，与电容的充电电压E₀和放电回路电阻R有关，具有如下矩阵向量形式：

方程组（4-23）就构成了具有铜盘—线圈结构的盘状推斥型快速电磁机构的电磁学和动力学基本方程组，通过迭代数值运算可求解出通电线圈电流、铜盘涡流、铜盘位移以及电磁推力的动态变化过程。

3.电磁力的数值计算方法

将方程组（4-23）中的电流方程（矩阵形式）经进一步整理，可得到时间域的递推算式：

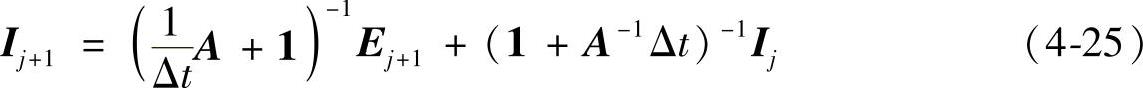
式中，1为N₁+1阶单位矩阵。令

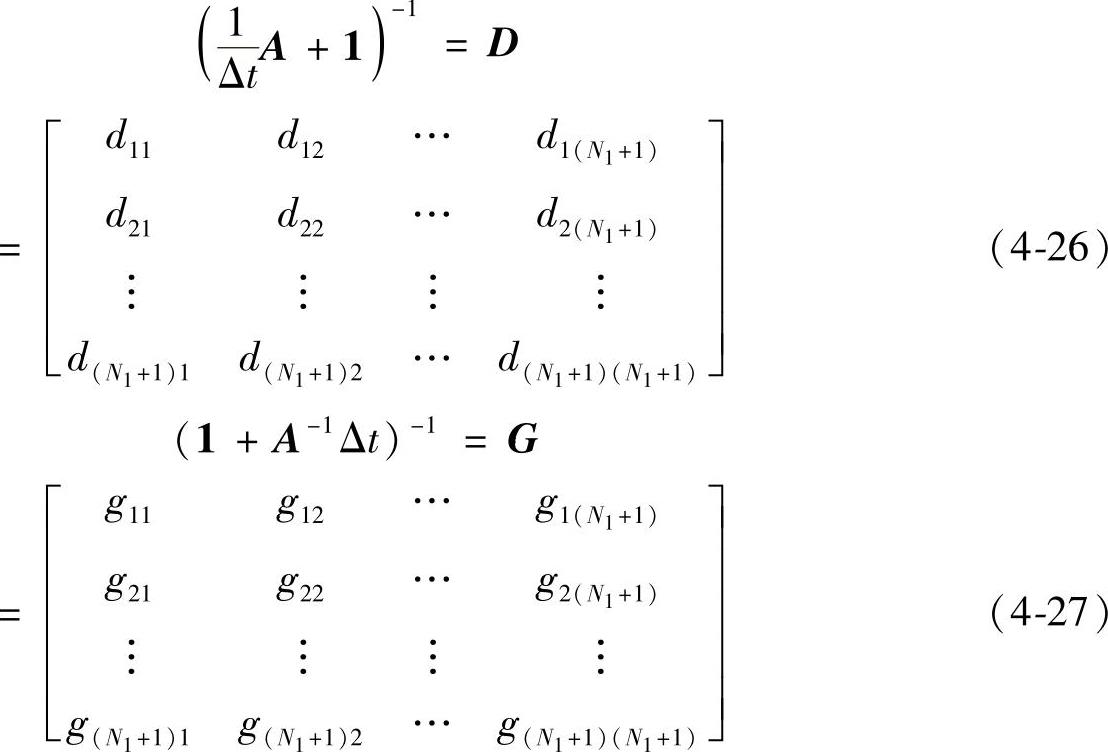
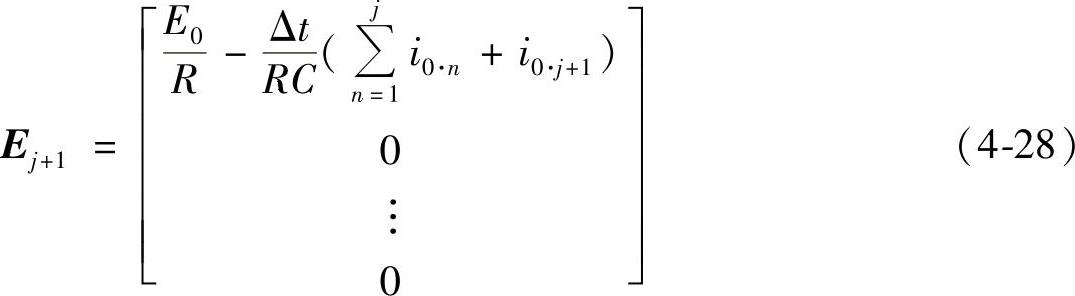
并令

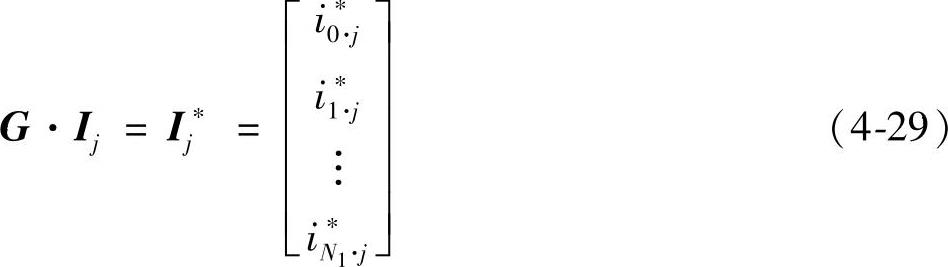
将式（4-26）～（4-28）和式（4-29）代入式（4-25），可得到计算各个电流瞬时值的迭代算式：

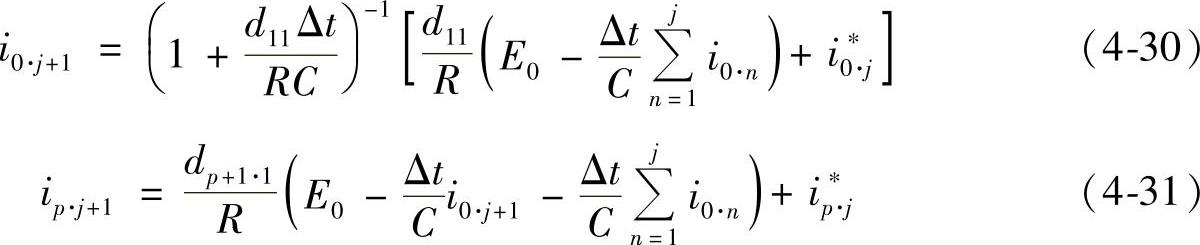
式中，p=1，2，…，N₁。

将式（4-30）、式（4-31）和式（4-23）中的电磁力方程和触头运动方程（离散化后）联立，就构成了具有铜盘—线圈结构的盘状推斥型快速电磁机构的电磁学和动力学基本计算方程组，可以迭代求解通电线圈电流、铜盘涡流、触头位移和电磁推力的动态变化过程，为电磁机构的动态仿真和综合优化提供了分析基础。

由于互感是位移x的函数，从式（4-23）可知，电流向量I是位移x和时间t的函数；电磁力F是电流向量I和位移x的函数；位移x是电磁力和阻力的函数。因此，电流向量I、电磁力F和位移x三者之间在触头运动的动力学过程中相互作用，都是时间和空间的函数，且存在严重的非线性关系，倘直接求解则非常困难。为此，提出基于时间和空间双层循环的迭代算法，其计算流程见图4-11所示。

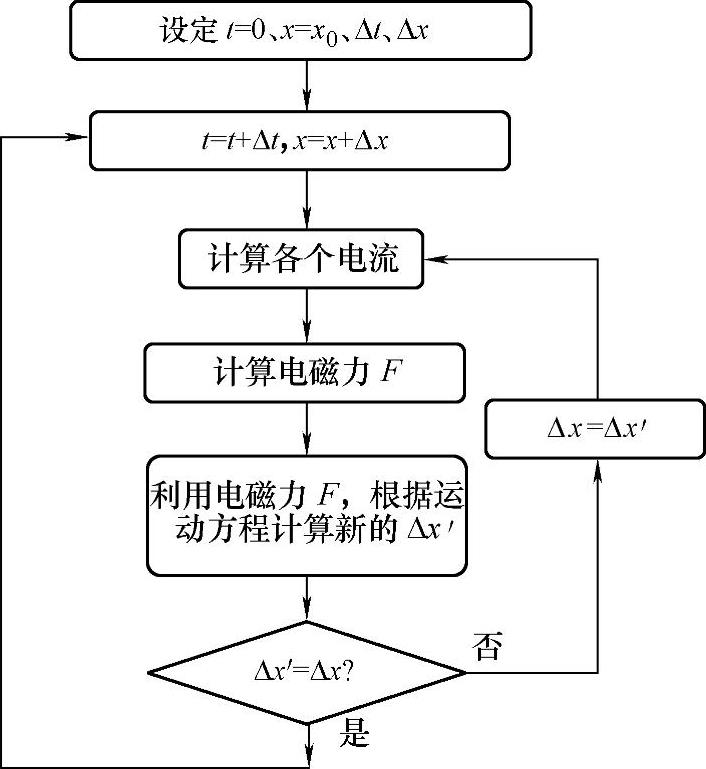
图4-11 双层迭代算法流程图

具体计算时，首先设定时间步长Δt，并假定第一个时间步长内的铜盘行程为Δx。计算此时的各个电流、互感及其导数、电磁力F，然后依据运动方程计算出该时间步长内新的行程Δx′。若Δx′不等于Δx，则令Δx=Δx′，重新迭代计算；否则，转入下一个时间步长，按上述规律依次循环计算。

4.2.1.3 机构参数优化仿真分析

依据前述的算法，通过改变某些重要参数的数值，可以优化盘状推斥型快速电磁机构的动态特性。在以下的仿真分析中，主要改变线圈、铜盘和放电回路的参数等，研究其对该型电磁机构暂态性能的影响，计算时以触头的关合过程为例。(www.daowen.com)

1.铜盘等效匝数的影响

在计算中将铜盘内连续的涡流分布等效为多个半径不等的电流环，因此从直观上看铜盘的等效匝数决定了计算精度，同时也影响到计算量。表4-3中给出等效匝数不同时对电磁力特性的影响。

表4-3 铜盘等效匝数的影响

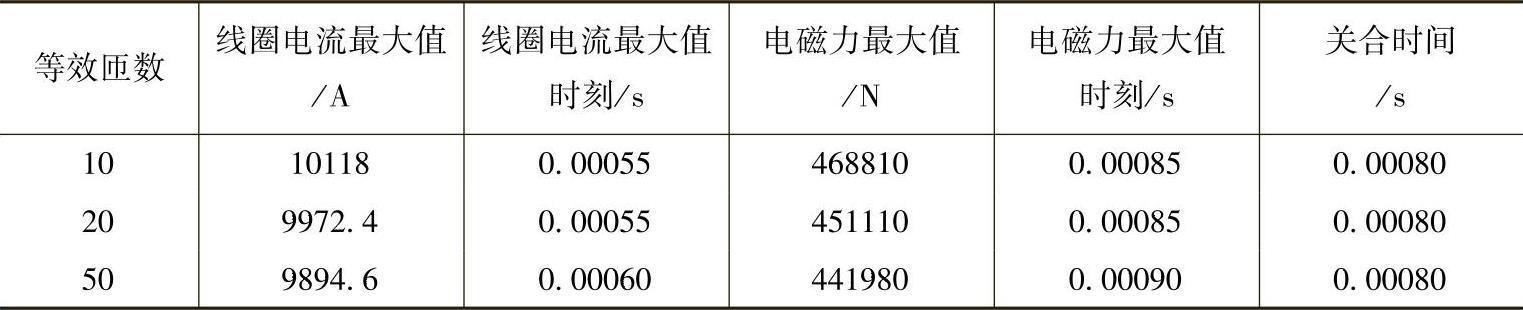
注：线圈为14匝，线圈和铜盘厚度均为5.3mm。

实际计算结果表明，在一定范围内铜盘等效匝数的多少对电磁力特性影响不大，其原因是：由等效多匝数改变为等效少匝数，电流将会随之增大，从而弥补了等效匝数减少对电磁力的影响，其综合效果基本不变。下面的计算中皆以铜盘等效为20匝为准，计算速度较快。

2.铜盘厚度的影响

为分析铜盘厚度对电磁力特性的影响，选取了4种不同厚度尺寸进行了仿真，线圈电流和电磁力等的计算结果如图4-12、图4-13和表4-4所示。

表4-4 铜盘厚度的影响

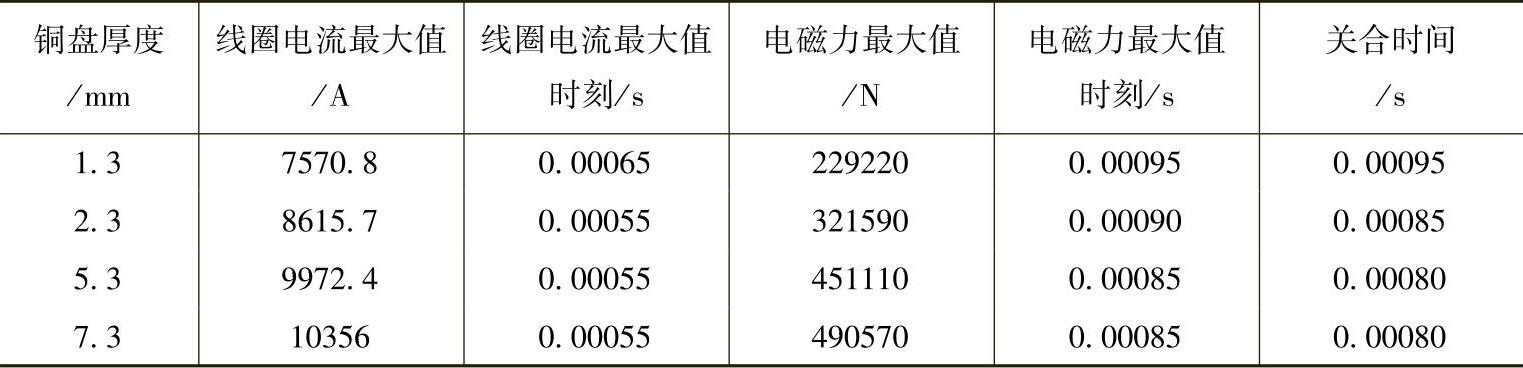
注：线圈为14匝，铜盘等效为20匝，线圈厚度为5.3mm。

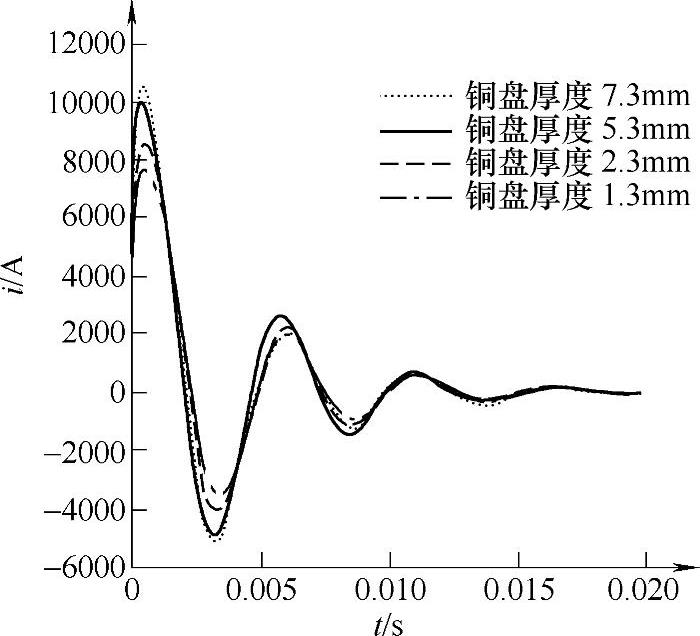
图4-12 铜盘厚度对放电电流的影响

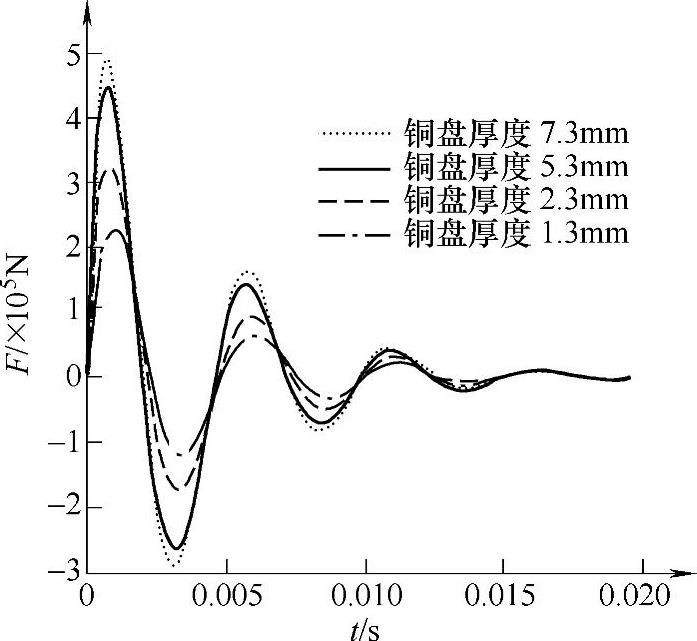
图4-13 铜盘厚度对电磁力的影响

由仿真结果可知，开始时随着铜盘厚度的增加，电流和电磁力增加较大，但当铜盘厚度增加到一定程度后，电流和电磁力趋于不变。分析其原因，一是厚度变化导致电阻和电感同时发生变化；二是集肤效应的影响变得显著。按照电磁场理论，集肤效应的渗透深度d可由式（4-32）确定：

式中，ω为信号角频率，μ为材料的磁导率，σ为材料的电导率。理论上讲，当铜盘厚度远小于2d时，可以忽略集肤效应的影响。若铜盘厚度过大，则集肤效应明显，而且增加了传动系统的质量，徒劳无益。

以14匝线圈时、充电电容为50000μF为例，可算出线圈电流的主要角频率含量为1240rad/s，进而得到渗透深度约为8.25mm。因此，当铜盘厚度远小于16.5mm时，可完全不考虑集肤效应的影响。但实际设计中考虑到铜盘要承受的机械强度以及需要较大的加速度，设计取其厚度为5.3mm，这时集肤效应影响不大。

3.线圈匝数的影响

当电容和充电电压值一定时，通电线圈的匝数决定了其电感的大小，既影响着放电周期的长短，同时也决定着线圈和铜盘之间的互感及其导数，即影响电磁推力的大小。因此，线圈匝数直接影响到电磁机构的速度和动作时间。图4-14和图4-15给出了线圈匝数分别为4、14、28、42匝时线圈电流和电磁力的动态变化情况，此时盘状线圈的等效半径分别为27.1mm、53mm、92.1mm、131.1mm。计算得到四种情况下开关触头的关合时间（10mm行程）分别为0.85ms、0.8ms、1.65ms、2.55ms。

由图4-14可见，随着线圈匝数的增加，线圈等效电感L增加，线圈电流的最大值i_0max减小，初始电流上升率di_0max/dt减小，放电周期T增大。若忽略电阻的作用，则上述各量由下列各式决定：

因此，仅从放电电流是否有利于电磁驱动而言，线圈的匝数愈小愈好，此时线圈电流大且放电周期短。但对于电磁力情况并非完全如此，其值随着线圈匝数的改变存在极大值现象，如图4-15所示。这是因为电磁力不仅与放电电流的大小有关，还取决于线圈和铜盘之间的互感导数。就此处分析结果而言，线圈匝数为14匝时电磁力最大。另外，对比几种情况下的关合时间可知，线圈匝数为14匝时关合时间也最短，为0.8ms。

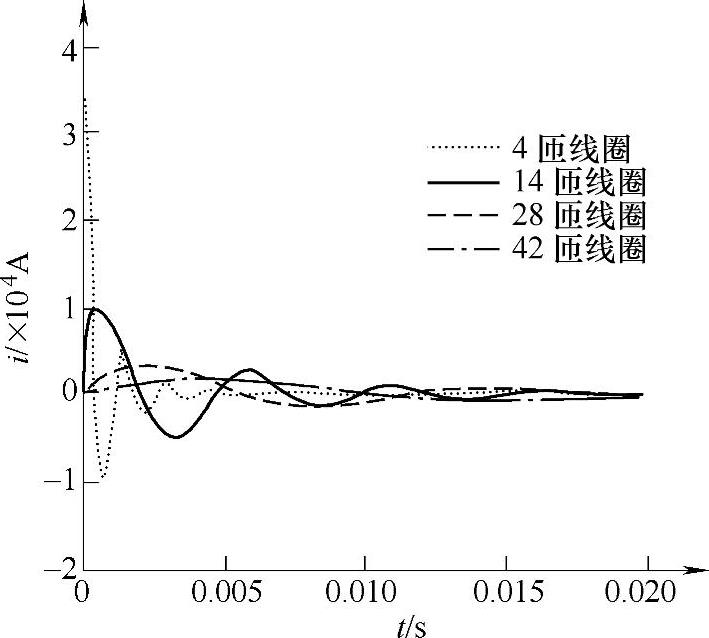
图4-14 线圈匝数对放电电流的影响

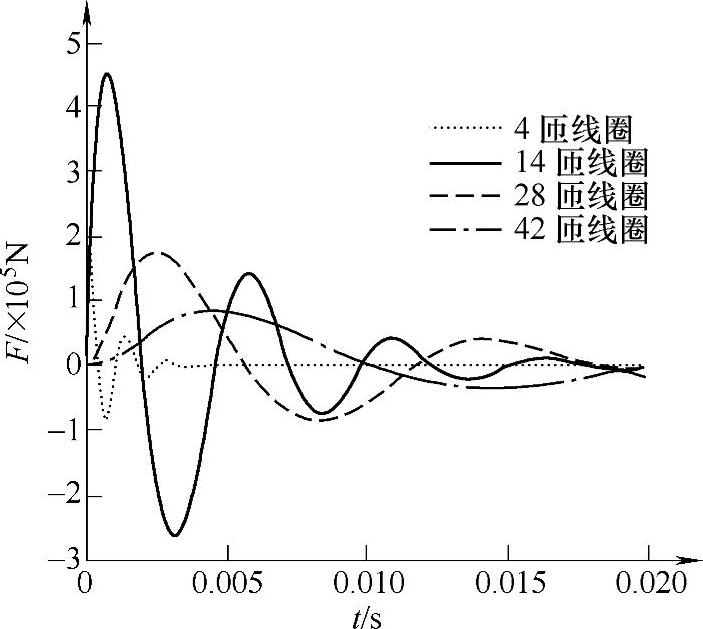
图4-15 线圈匝数对电磁力的影响

4.线圈导线厚度的影响

改变线圈导线厚度的计算结果如图4-16、图4-17和表4-5所示。尽管随着导线厚度的增加可以提高放电电流和电磁力的大小，但到达最大值的时间基

表4-5 线圈导线厚度的影响

注：线圈为14匝，铜盘等效为20匝，铜盘厚度为5.3mm。

本不变，且触头的关合时间也变化不大。因此，通过改变线圈导线的厚度来提高快速开关的速度，效果并不明显。

5.线圈与铜盘相对大小对电磁机构的影响

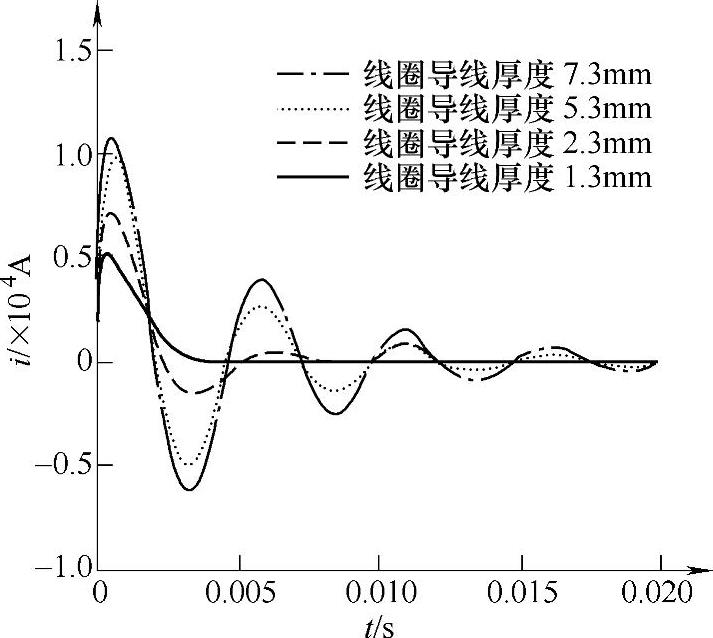
图4-16 线圈导线厚度对放电电流的影响

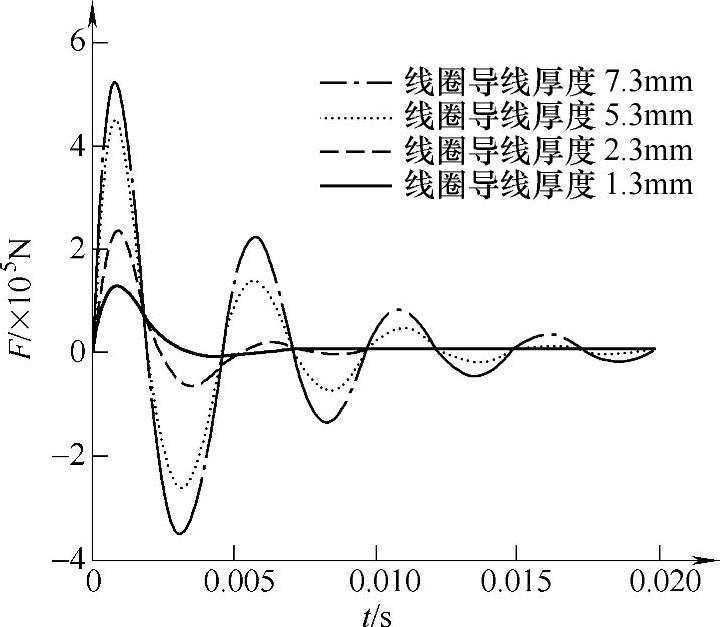
图4-17 线圈导线厚度对电磁力的影响

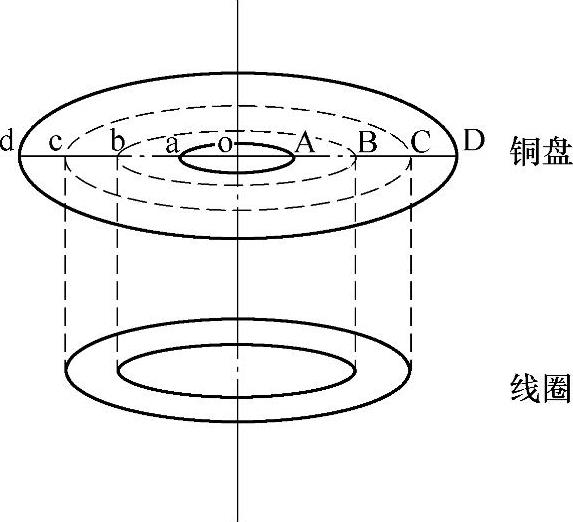
图4-18 铜盘与线圈相对大小示意

为便于分析此问题以获得较一般的设计指导原则，仿真时采用以下基本数据：盘式线圈共7匝，导线宽度为1.85mm，线圈中间空心半径为15mm，外半径为33mm；铜盘涡流等效为60匝，每匝宽度为1.75mm，铜盘中间空心半径为5mm，外半径为53mm。线圈与铜盘的相对大小示意如图4-18所示，从a到d（或从A到D）为铜盘沿半径等效涡流第1匝到第60匝；Bb对应于盘式线圈的内直径，Cc对应于其外直径。相应的计算结果如图4-19～图4-22所示。

由图4-19可知，铜盘等效涡流沿半径第10至25匝的电流值较大，其中第15匝的感应电流负峰值最大。此时对应的铜盘半径范围为13mm至27mm，正是与线圈相对面积基本重合的部分（由圆Bb和Cc组成的圆环BbCc）。在未重合部分（内圆环AaBb和外圆环CcDd），感应的涡流较小，效率不高。

在铜盘的三个部分，即内圆环AaBb、与线圈重合圆环BbCc和外圆环CcDd，相应各匝感应的涡流曲线如图4-20、图4-21和图4-22所示。结果表明，内圆环和外圆环中均感应出正的（与线圈电流同向）涡流，尤其内圆环的正值电流很大，这意味着它们将对电磁机构贡献电磁吸力，而快速开关是需要电磁斥力来工作的。

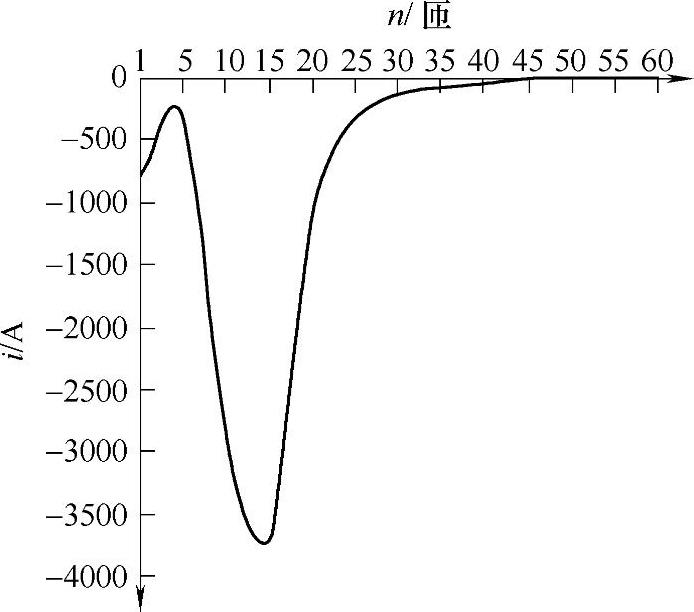
图4-19 铜盘各匝等效涡流负峰值的变化情况

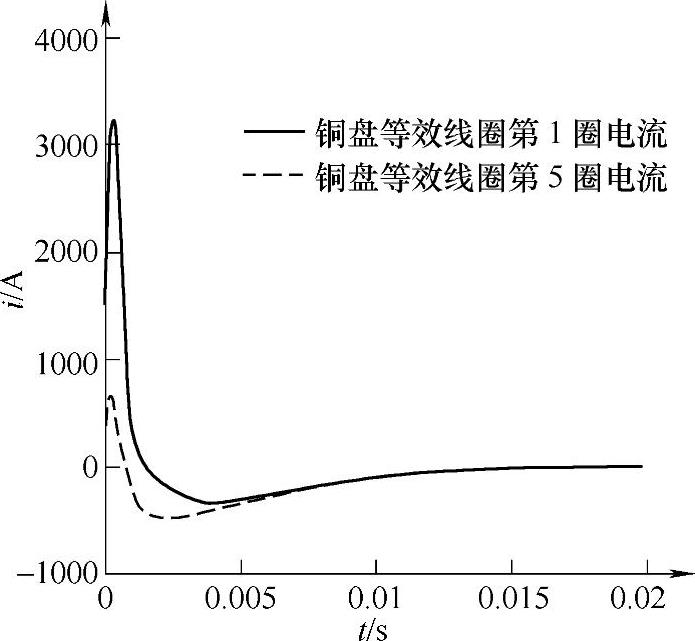
图4-20 铜盘等效第1、5匝涡流

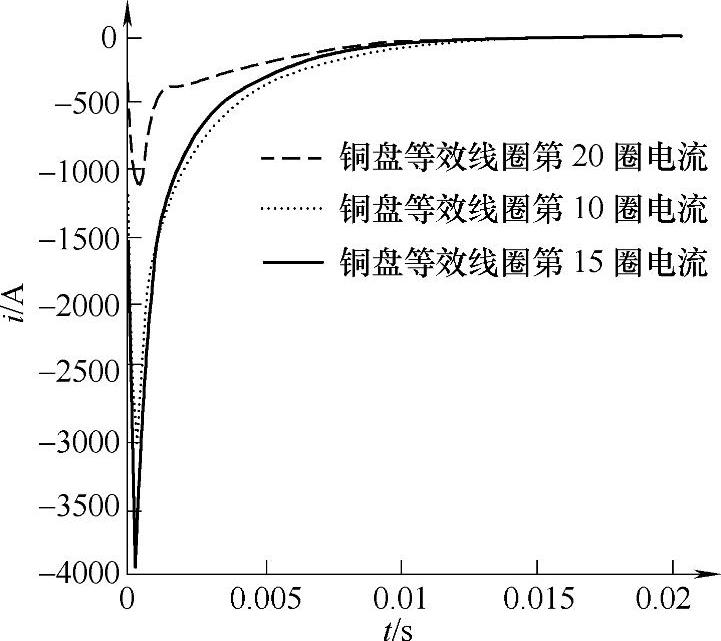
图4-21 铜盘等效第10、15、20匝涡流

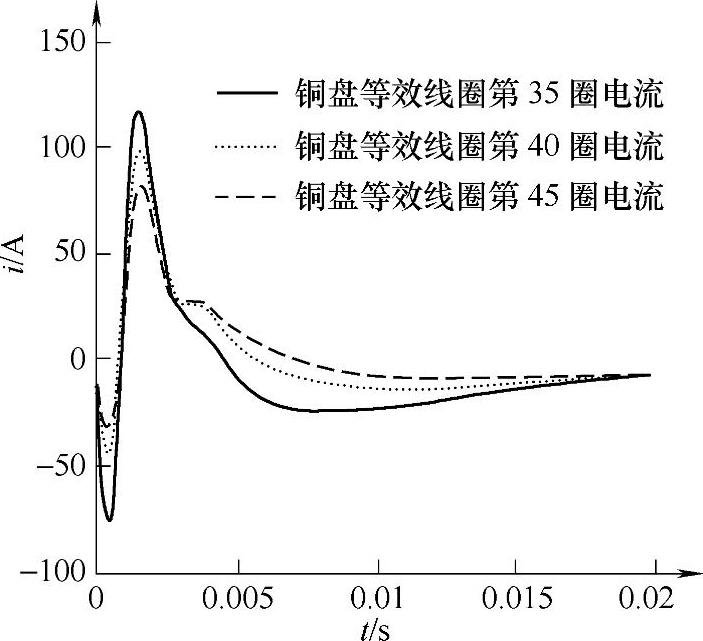
图4-22 铜盘等效第35、40、45匝涡流

由以上分析可得出如下结论：相对于盘式线圈的大小，铜盘的尺寸设计得太大或者太小，该型电磁机构的效率都不高，反而会起负作用，应当尽量设计铜盘与线圈的空间尺寸相一致。

铜盘厚度和线圈导线厚度对电磁力和电流等参数有一定影响，但对分、合闸时间影响不大；因此，综合考虑机械强度问题以及产生较大电磁力，设计时可适当减小铜盘及线圈导线厚度。在电容及其充电电压一定时，盘式线圈的匝数直接决定着放电周期，进而影响开关的分、合闸时间，应根据仿真分析选取最优的线圈匝数以获得较大的电磁力和较短的动作时间。当铜盘与线圈的空间尺寸不一致时，两者重合部分对机构的贡献最大，非重合部分反而具有负作用；实际设计时应尽量使两者大小对应，以显著提高该型电磁机构的效率。

4.2.1.4 双稳弹簧式保持机构

除了利用通电线圈与铜盘感应涡流间产生的脉冲电磁力实现开关操动机构的快速驱动外，如何保持开关的分断与关合稳态位置，也是机械设计的关键所在。文献[1]中曾采用叠簧结构，但实验表明其机械稳定性欠佳，为此提出了一种弹簧式双稳结构，如图4-23所示。双稳弹簧及其连杆的运动示意如图4-24所示。

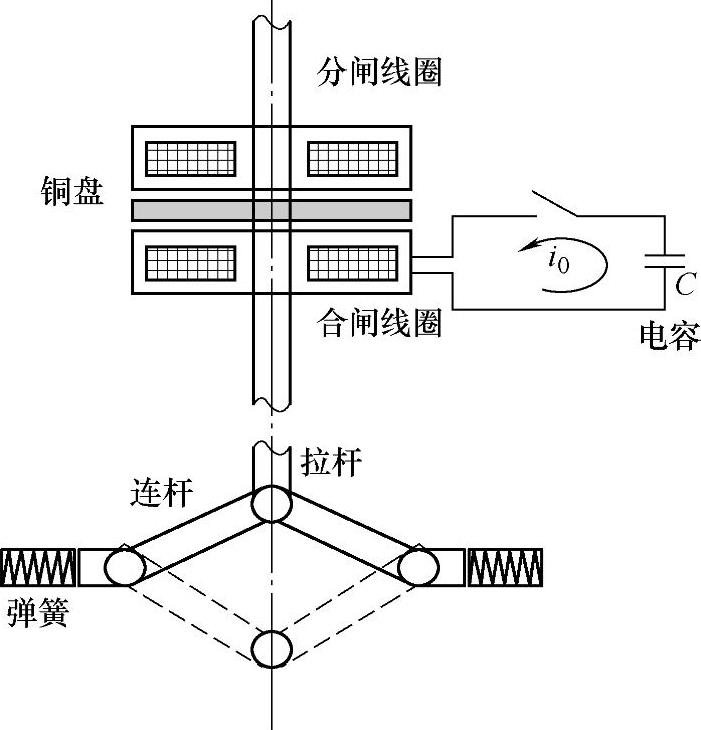
图4-23 双稳弹簧式盘状推斥型电磁机构示意

在触头关合过程中，双稳弹簧的作用力是非线性变化的，分析较为复杂。但该双稳弹簧具有对称性，如图4-24a所示，因此其受力分析可简化为椭圆规机构，如图4-24b所示。其中，f_t为弹簧力，d_t为该力的位移微分；f_z为弹簧力在垂直方向上的分力，d_z为该力的位移微分。根据能量守恒，有f_td_t=f_zd_z，由此可得f_z/f_t=d_t/d_z=tanα，最后经推导可得到式（4-36）所示的形式。其中，f_z（x）为弹簧力在垂直方向上的分力；f_c为拉杆处于水平位置时弹簧的弹力；l₀为拉杆长度；k为弹簧的弹性系数；x为动触头位移；l_ae为e和a两点之间的距离，等于触头行程的一半。

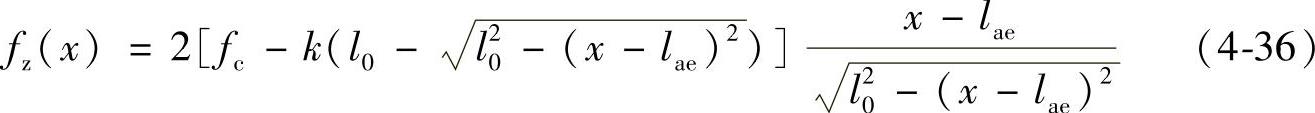
式（4-36）中方括弧内的第二项，表示因弹簧被拉长使弹簧力减弱的部分。

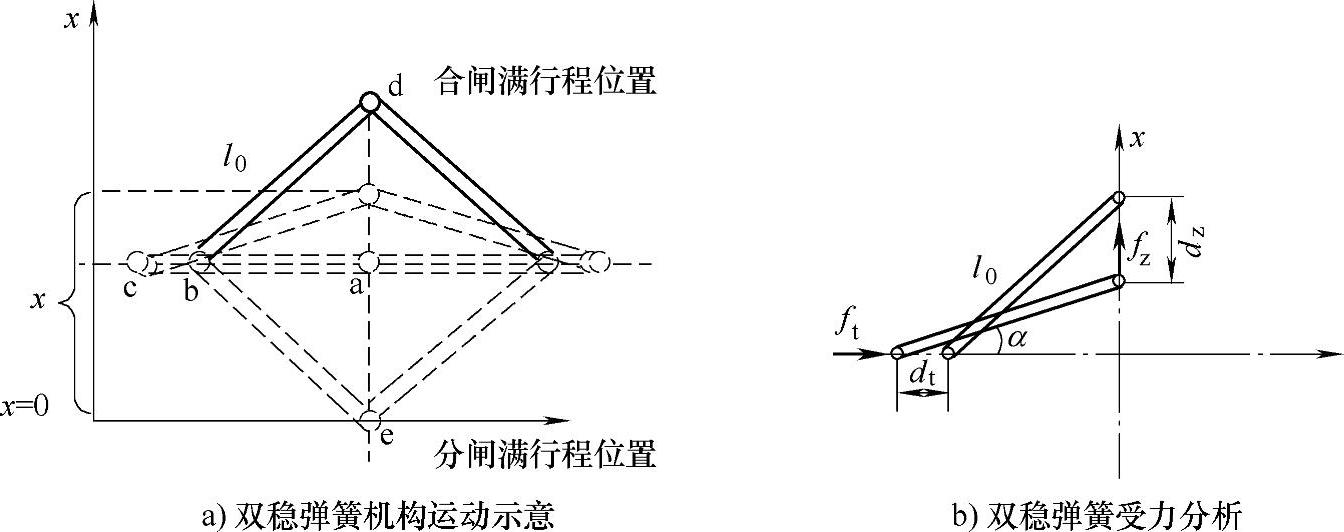
图4-24 双稳弹簧运动及受力分析示意

对于图4-23所示的电磁机构，要想获得符合实际操作要求且又经济、可靠的性能指标，需要优化的设计参数很多，如通电线圈的结构参数（匝数、导线截面等），铜盘的结构尺寸（半径、厚度等），放电回路的有关参数（电容量、充电电压、放电回路电阻等），这些须借助于计算机仿真来实现。在下面的仿真和优化分析中，将摒弃那些对电磁机构性能影响较小的因素，以缩小优化范围。仿真分析将依据下述的基本设计参数，通过改变某些主要参数实现机构的优化设计。

4.2.1.5 算例

基于前述的仿真分析，并进行优化设计，这里给出了一个带有双稳弹簧结构的10kV等级快速真空断路器的关合过程算例。其中，铜盘半径为35mm，厚度为5.3mm，铜电阻率取1.69×10^-8Ω·m；线圈共14匝，等效盘状半径为39mm，导线截面厚度为5.3mm，截面宽度为1.85mm；铜盘与线圈的初始间距为3mm；开关动触头行程为10mm；拉杆半径为15mm；铜盘和连杆系统的总质量为2.5kg；真空开关自吸力为50N；放电回路电容为50000μF，充电电压为160V。

利用前面给出的迭代算法，计算得到图4-25、图4-26和图4-27所示的曲线。结果表明，开关合闸时间可以达到0.23ms，具有非常好的快速特性。分闸过程的分析与此类似，不再详述。

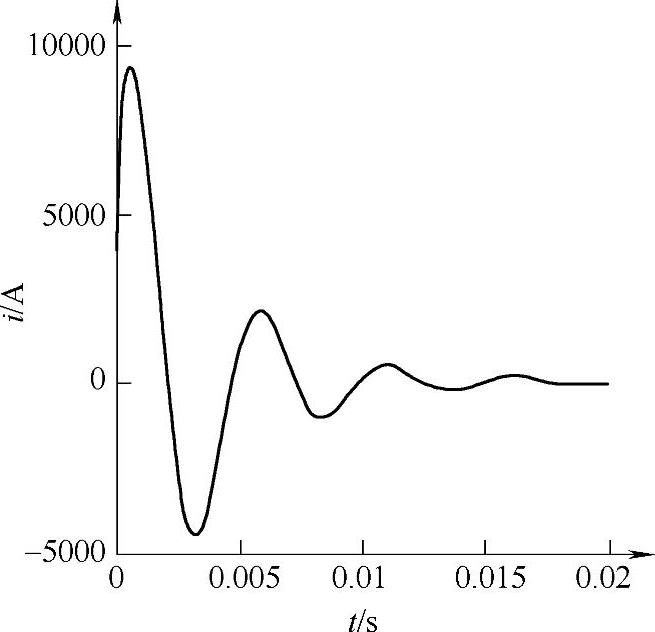
图4-25 关合过程线圈电流的变化曲线

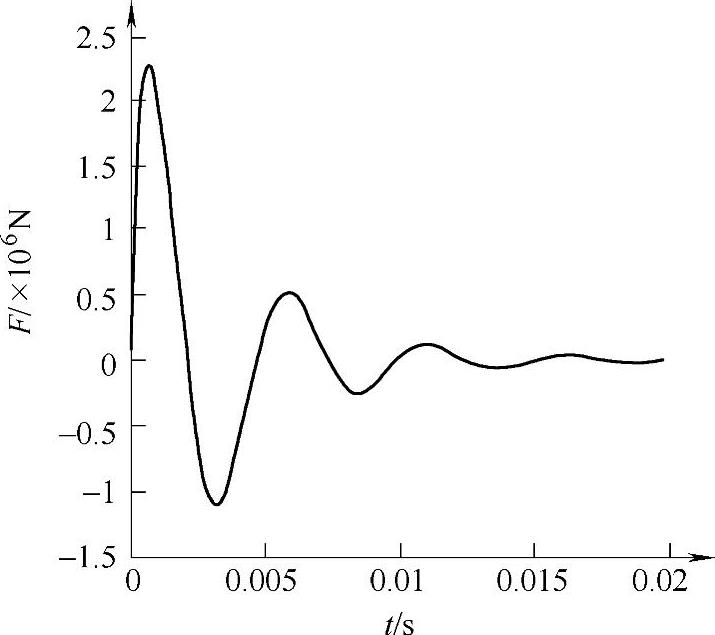
图4-26 关合过程电磁力的变化曲线

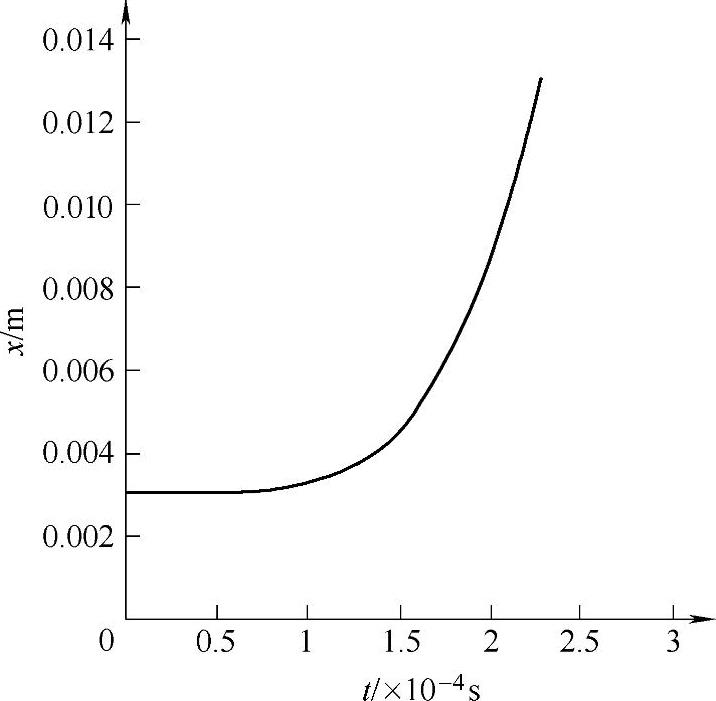
图4-27 动触头行程变化曲线

必须指出，此处的仿真计算与优化分析中并没有考虑触头碰撞时的振动现象，而在实际快速开关中，由于脉冲电磁力相当大，必然伴有振动过程。

4.2.1.6 小结

针对盘状推斥型快速电磁机构，给出一种基于时间和位移双层循环的离散迭代算法，此算法可用于盘状推斥型电磁机构的仿真分析和综合优化设计。通过仿真详细研究了不同的结构参数对该型电磁机构动态特性的影响，并给出了一般性的优化设计指导原则。例如，实际设计时可适当减少铜盘及线圈导线厚度；当铜盘与线圈的空间尺寸一致时电磁机构效率最高；等等。提出采用一种保持快速开关合、分闸状态的弹簧式双稳结构，并用优化分析的参数在算例中计算了触头的关合过程，合闸时间可达到0.23ms。尽管该型电磁机构的拓扑比较简单，但数学模型较为复杂，进行动态过程计算时需要复杂的数值算法，并不利于实时控制。