在保压分析中，熔体密度描述的准确性对保压过程的模拟精度影响很大。塑料材料的密度是压力和温度的函数，通常用压力-体积-温度（Pressure-Volume-Temperature，简称PVT）关系图来表示熔体的状态方程^[288]。图11-6所示为典型的无定形塑料和半结晶型塑料的PVT关系曲线，其中，T_g、T_m分别代表无定形塑料的玻璃化转变温度和半结晶型塑料的结晶温度。

常用的描述熔体密度的状态方程有单域Spencer-Gilmore（简称S-G）状态方程^[289]和双域Tait状态方程^[280]两种。

单域Spencer-Gilmore状态方程

式中，p_c（Pa）、ρ_c（kg/m²）为材料常数；R为摩尔气体常量[J/（mol·K）]。

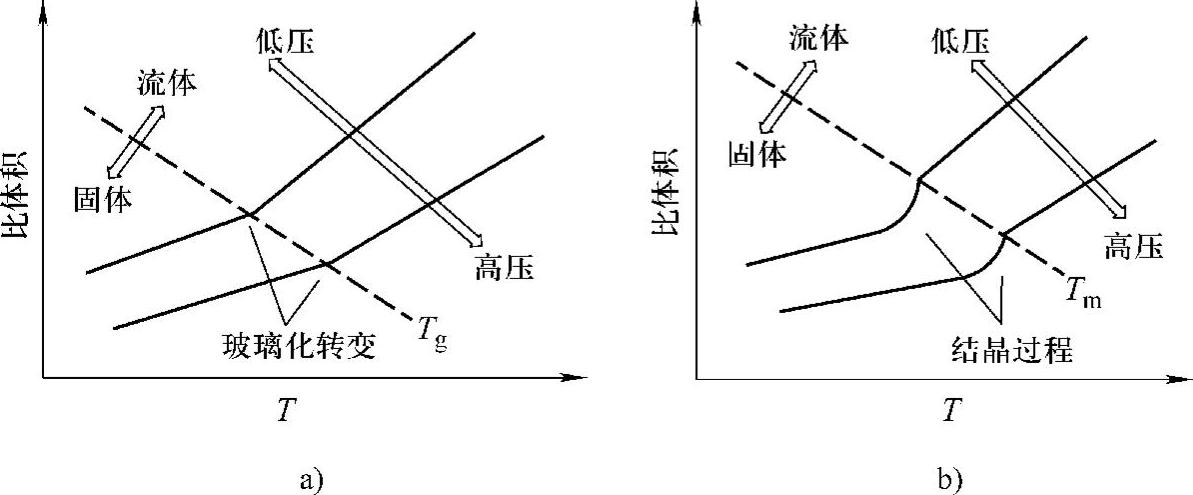
图11-6 典型的无定形塑料和半结晶型塑料的PVT关系图

a）无定形塑料 b）半结晶型塑料

双域Tait状态方程(www.daowen.com)

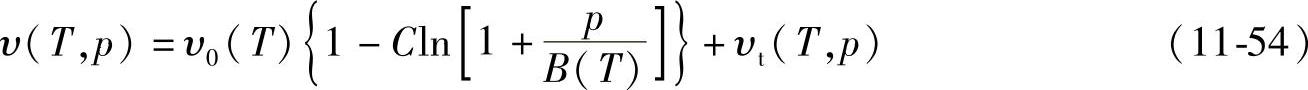
其中

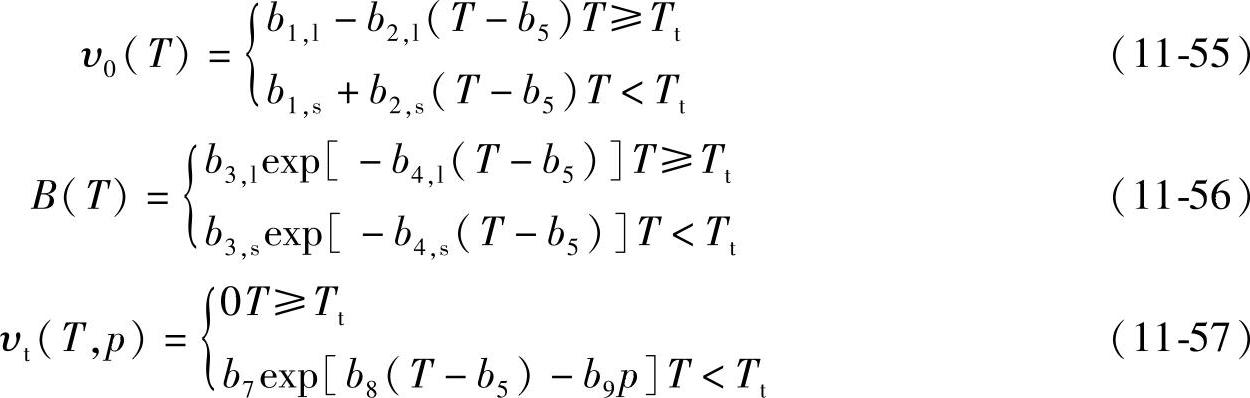
式中，υ为比体积（m³/kg）；C=0.0894；b₁～b₉为材料常数；T_t为熔体的相变温度（K），对于结晶型聚合物为结晶温度，对于非结晶型聚合物为玻璃化转变温度；下标l、s分别代表液态和固态时的参数值。

假定转换温度T_t为压力的线性函数，则有

T_t （p）=b₅+b₆p（11-58）

同单域S-G方程相比，双域Tait方程同时给出了塑料材料在固态和熔融态的密度分布，能更准确地描述聚合物材料的密度变化。但是，对于快速热循环注塑过程而言，在充填和保压过程中，模具型腔的温度一直保持在熔体的玻璃化转变温度以上，型腔内的熔体一直处于熔融态，不存在相变问题。因此，这里采用更易于实现的单域S-G状态方程来描述熔体密度与压力和温度之间的关系。