通过引入通用张量ϕ，方程式（11-1）～式（11-3）可统一写成如下形式

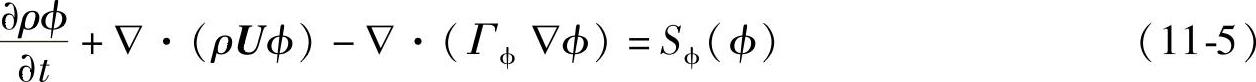
式中，Γϕ为扩散系数，Sϕϕ为源项。式（11-5）中，左边第一项为瞬态项，表示单位体积内ϕ的变化率，左边第二项为对流项，表示单位体积内对流产生的ϕ的流出率，左边第三项是扩散项，代表由扩散引起的ϕ的变化率，右边为源项，表示单位体积内ϕ的产生或消失量。

将式（11-5）沿单元P的控制体积V_P和时间t积分，得到积分形式的通用方程

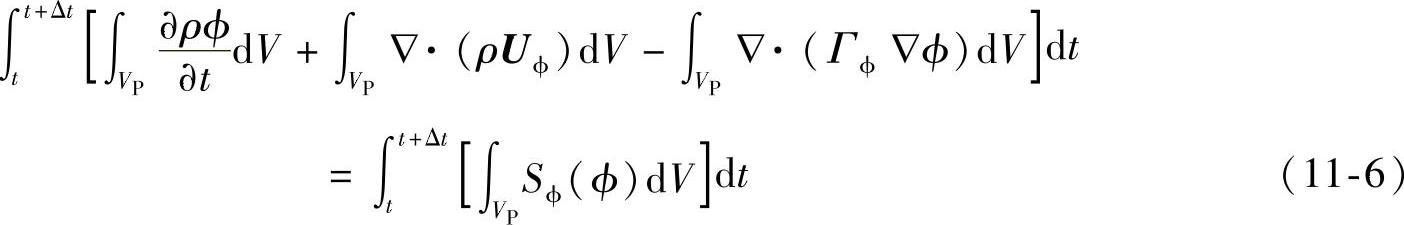
采用静止的同位网格系统，假设变量ϕ沿控制体积线性分布，用欧拉隐式算法处理瞬态问题，将源项线性处理Sϕ（ϕ）=S_u+S_Pϕ，根据高斯散度定理，可得到半离散形式的控制方程^[265]

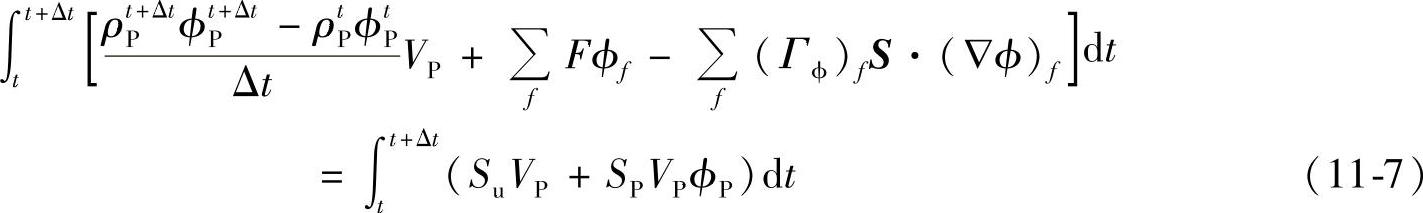
式中，F为通过单元面f的质量流率F=S·（ρU）f；S为单元面的外法向向量；上标t、t+Δt分别代表t和t+Δt时刻的变量值；下标P、f分别代表单元P和单元面f上的变量值。

假设变量ϕ在时间t到t+Δt内的变化规律符合下面的方程(www.daowen.com)

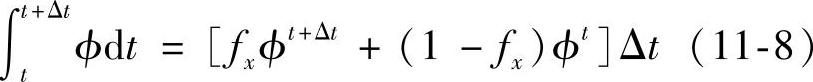
式中，f_x是一个在0到1之间变化的加权因子。

假设密度和扩散强度不随时间变化，即ρ^t=ρ^t+Δt=ρ，Γ^t=Γ^t+Δt=Γ。当f_x分别取0、0.5和1时，变量ϕ随时间的变化关系如图11-2所示。

当f_x=1时，为全隐式离散模式，在时间上为一阶精度，不如Crank-Nicholson方法精确。但是与显式离散模式和Crank-Nicholson模式相比，全隐式算法能够兼顾解的稳定性和物理上的真实性。因此这里令f_x=1，得到全隐式算法离散后的通用控制方程如下

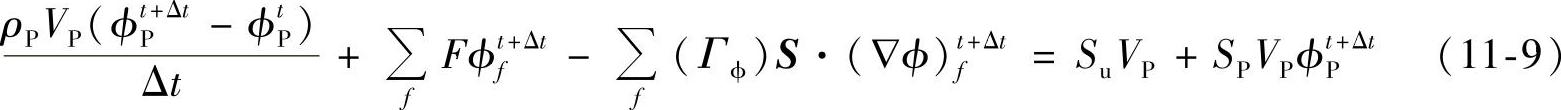
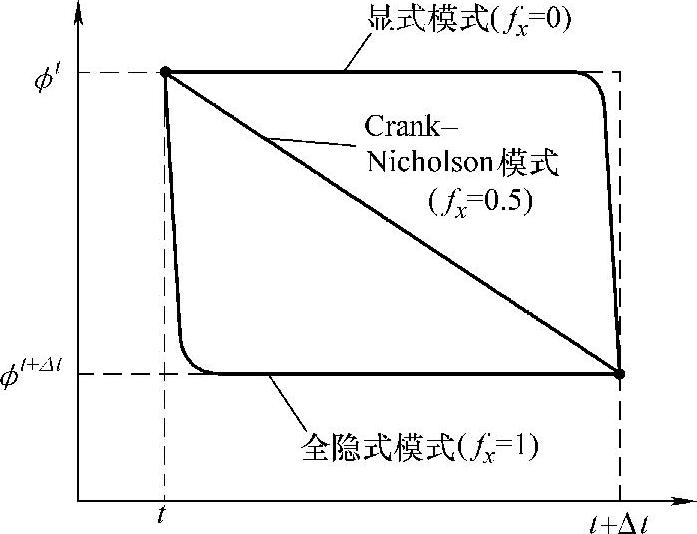
图11-2 f_x分别取0、0.5和1时，变量ϕ随时间的变化关系^[266]