图9-6所示为试验测得的型腔表面上各数据采集点的典型温度响应曲线。从图中可以看出，随着循环加热冷却连续进行，模具型腔表面温度在周期性的高低波动中不断升高，并逐渐趋于稳定，最终达到平衡状态。对于相同的模具加热时间t_h，随着模具冷却时间t_c的增大，模具型腔表面温度变化达到平衡状态所需要的加热冷却循环次数逐渐减小，达到平衡状态后型腔表面的周期性最高温度T_h和最低温度T_l均逐渐降低；而当模具冷却时间相同时，随着模具加热时间增大，模具型腔表面温度变化达到平衡状态所需要的加热冷却循环次数逐渐增大，达到平衡状态后型腔表面的周期性最高温度T_h和最低温度T_l均逐渐升高。

图9-6 试验测得的型腔表面上各数据采集点的典型温度响应曲线

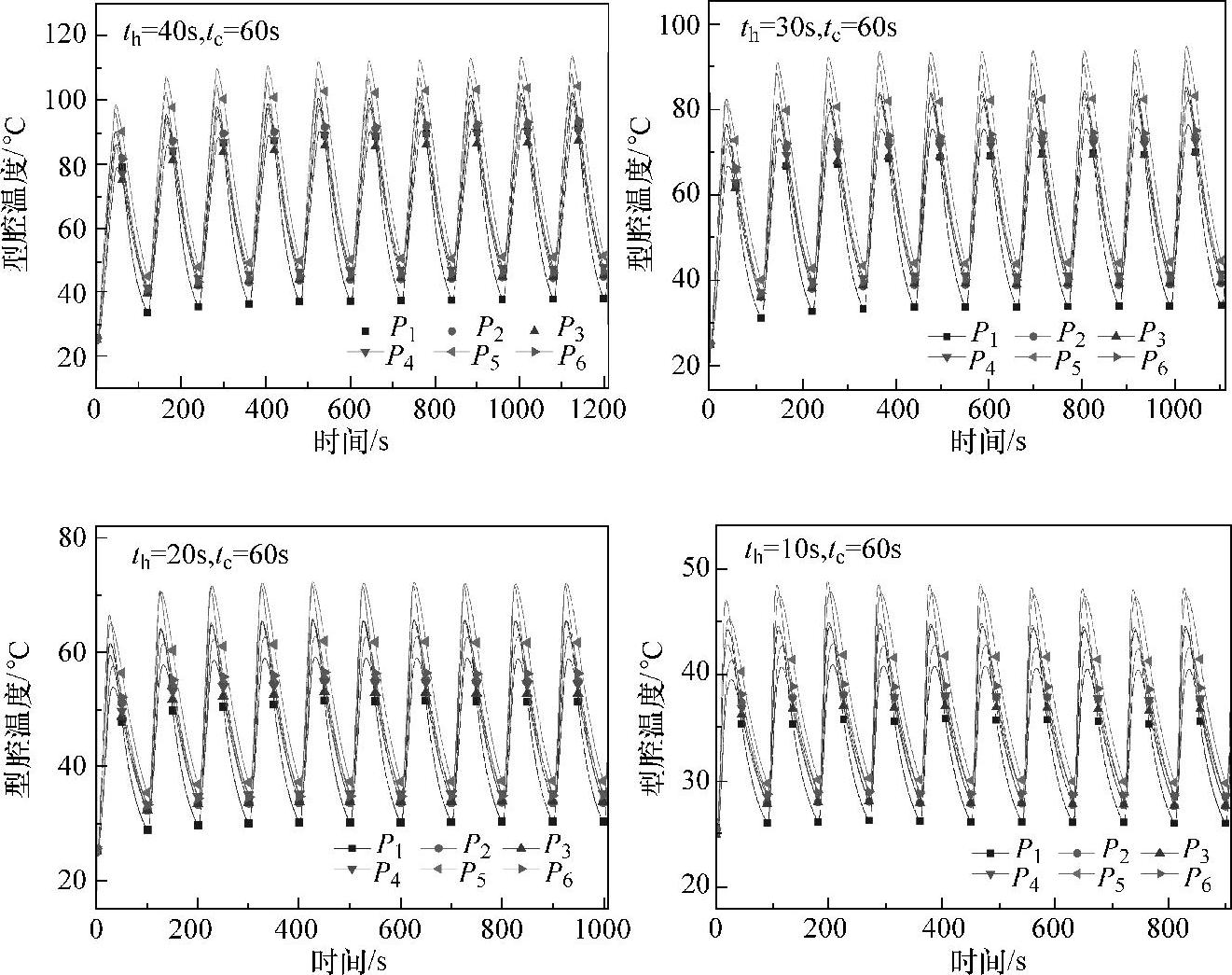
图9-6 试验测得的型腔表面上各数据采集点的典型温度响应曲线（续）

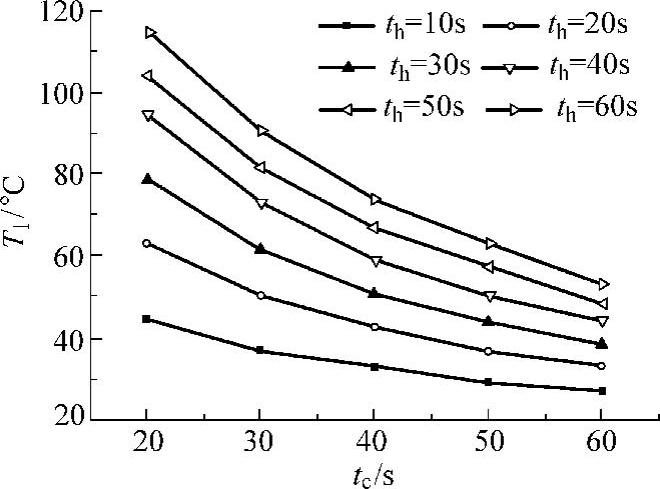
图9-7和图9-8所示分别为试验获得的模具加热时间对型腔表面周期性最高温度T_h和最低温度T_l的影响规律。随着模具加热时间增大，模具型腔表面周期性的最高温度T_h和最低温度T_l均逐渐升高，但升高速度均逐渐减小，且最高温度T_h的增长幅度大于最低温度T_l的增长幅度，这表明型腔表面温度的波动范围也逐渐增大。另外，模具冷却时间越短，模具加热时间对模具型腔表面周期性最高温度和最低温度的影响越大，即随着模具加热时间增大，两者的增长幅度相对较大。图9-9和图9-10所示分别为试验获得的模具冷却时间对型腔表面周期性最高温度T_h和最低温度T_l的影响规律。随着冷却时间增大，模具型腔表面周期性的最高温度T_h和最低温度T_l均逐渐降低，但降低速度逐渐减小，由于周期性最高温度T_h的降低幅度小于周期性最低温度T_l的降低幅度，这表明模具型腔表面温度的波动范围逐渐增大。另外，当模具冷却时间改变时，模具加热时间对周期性最高温度T_h的影响程度基本一致，即

图9-7 加热时间对型腔表面周期性最高温度的影响

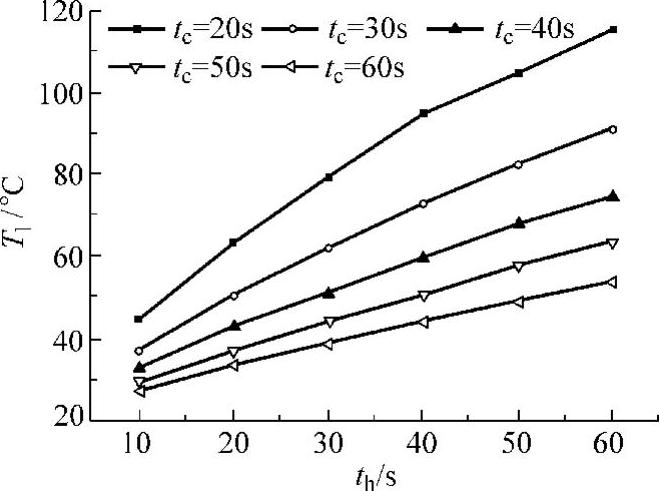
图9-8 加热时间对型腔表面周期性最低温度的影响

随着加热时间增大，T_h的降低幅度基本相同，但随着模具冷却时间增大，模具加热时间对周期性最低温度T_l的影响程度会越大，即随着模具加热时间增大，T_l的减小幅度增大。

根据热响应试验结果，绘制了描述模具加热时间和模具冷却时间与T_h和T_l关系的三维曲面，分别如图9-11和图9-12所示。从图中可以看出，模具加热时间对T_h和T_l的影响程度显著高于模具冷却时间对T_h和T_l的影响程度。这表明，当模具型腔表面温度需要大范围调整时，应以调节模具加热时间为主；而当对模具型腔表面温度进行小范围调整时，则应当以调节模具冷却时间为主。

图9-9 冷却时间对型腔表面周期性最高温度的影响

(www.daowen.com)

图9-10 冷却时间对型腔表面周期性最低温度的影响

图9-11 描述模具加热时间和冷却时间对型腔表面周期性最高温度影响的三维曲面

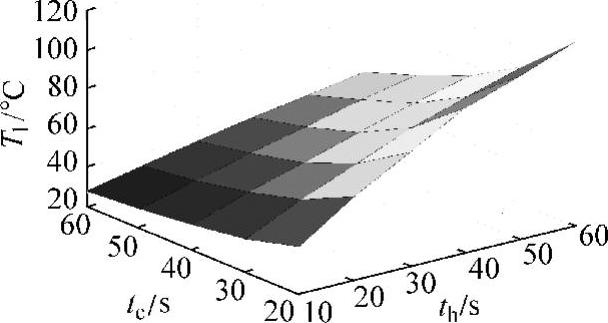
图9-12 描述模具加热时间和冷却时间对型腔表面周期性最低温度影响的三维曲面

根据试验数据，利用最小二乘法进行非线性回归分析，拟合建立了描述模具型腔表面周期性最高温度和最低温度的数学模型，其表达式如下

T_h=59.2874-0.0152t²_h+0.0149t²_c+3.4230t_h-1.5043t_c-0.0108t_ht_c（9-1）

T_l=60.8361-0.0048t²_h+0.0191t²_c+2.0839t_h-1.8115t_c-0.0215t_ht_c（9-2）

利用式（9-1）和式（9-2），可方便地预测不同模具加热时间和冷却时间组合下模具型腔表面温度的具体波动范围。更为重要的是，在快速热循环注塑工艺要求的型腔表面温度波动范围已知的情况下，通过求解由上述两式组成的二元二次方程组即可计算得出合理的模具加热时间和冷却时间，从而使得快速热循环注塑工艺参数设定更有针对性，有效地简化了快速热循环注塑工艺调试过程。

图9-13所示为试验获得的模具型腔表面温度响应曲线。从图中可以看出，模具温度进入稳定周期性变化以后，型腔表面的最高温度和最低温度与目标控制温度具有很好的一致性。实际测量的型腔表面最高温度与假定的型腔表面最高温度之间的最大相对误差仅为3.1%，实际测量的型腔表面最低温度与假定的目标最低温度之间的最大相对误差仅为2.8%，均在工程计算允许的范围内，从而验证了所建立的数学关系模型的有效性和准确性。

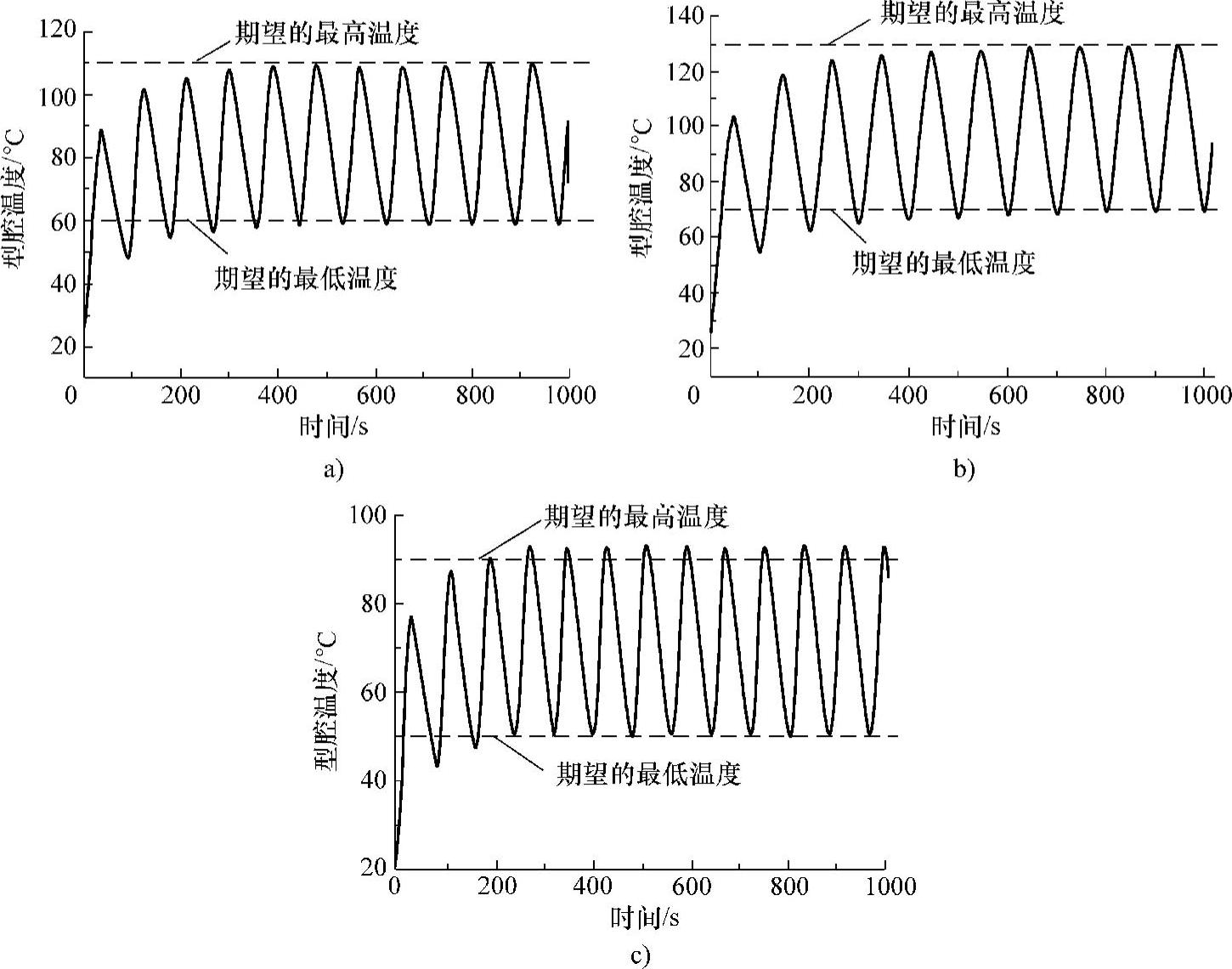
图9-13 由验证试验测得的型腔表面温度响应曲线

a）第一组 b）第二组 c）第三组