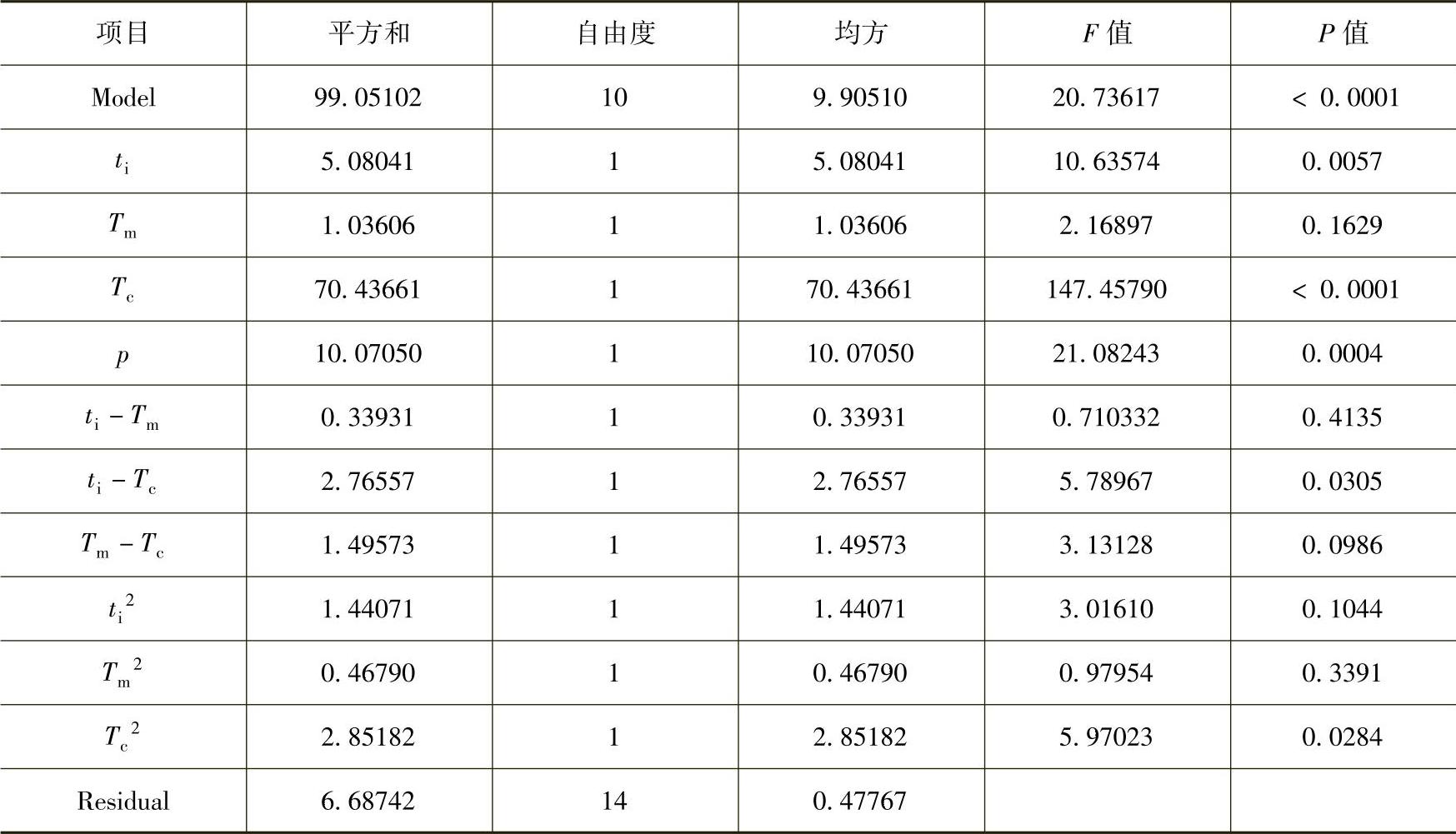
根据表8-8中的试验数据，利用基于最小二乘法的回归分析，拟合可预测塑件最大Z向翘曲变形和缩痕深度的二次多项式数学模型，分别见式（8-5）和式（8-6）。表8-9和表8-10分别给出了关于塑件翘曲变形量和缩痕深度多项式数学模型的ANOVA分析结果。从表中数据可以看出，回归模型的F值分别为20.74和346.99，这表明拟合得出的多项式数学模型在设计空间范围内是显著的。另外，从各项的P值可以看出，线性项（t_i、T_c、p）、交叉项（t_i-T_c、T_m-T_c）以及二次项（T²_c）对翘曲变形量具有显著影响，而线性项（t_i、T_c、p）、交叉项

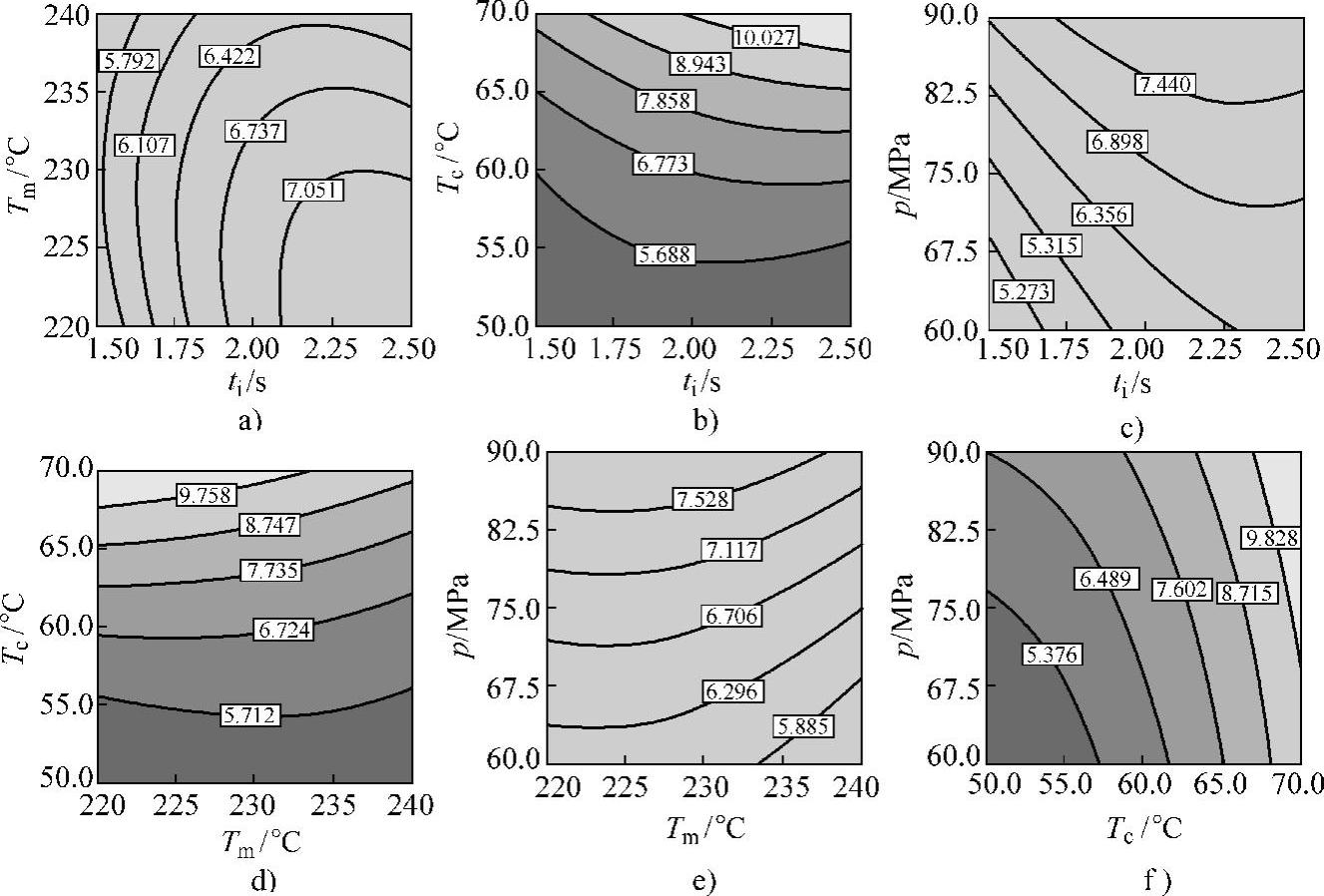
图8-36 模拟计算获得的快速热循环注塑工艺参数对塑件翘曲变形的影响

a）t_i和T_m b）t_i和T_c c）t_i和p d）T_m和T_c e）T_m和p f）T_c和p

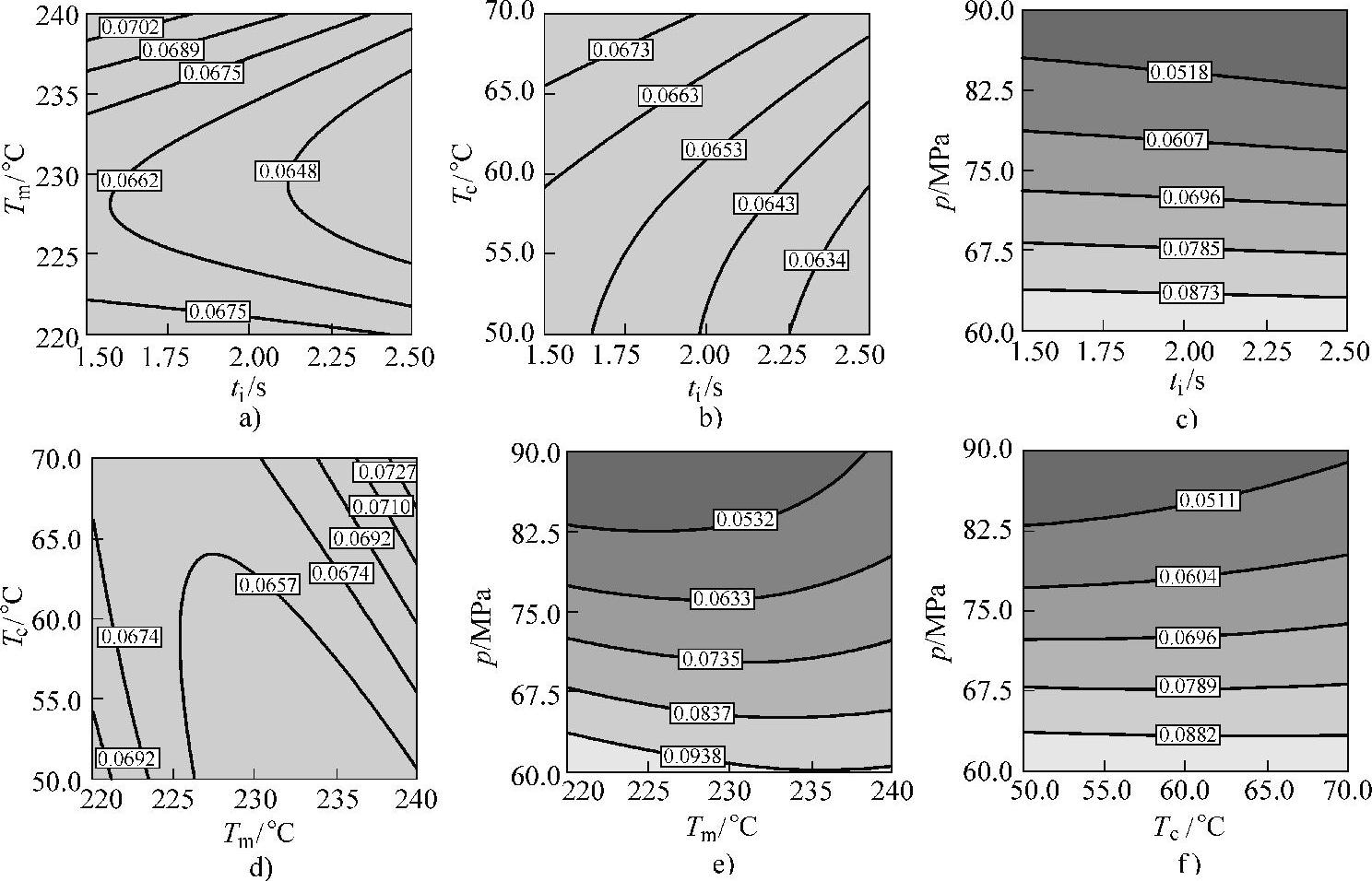
图8-37 模拟计算获得的快速热循环注塑工艺参数对塑件缩痕深度的影响

a）t_i和T_m b）t_i和T_c c）t_i和p d）T_m和T_c e）T_m和p f）T_c和p

（T_m-T_c、T_m-p、T_c-p）以及二次项（T²_m、p²）对缩痕深度具有显著影响。(www.daowen.com)

为了验证所建立二次多项式数学模型的有效性，在设计空间范围内任意设定三组未包含在表8-8中的工艺变量组合，通过执行注塑模拟分析，获得塑件最大Z向翘曲变形和缩痕深度，并与所构建多项式数学模型的预测结果进行比较，相关结果见表8-11。通过对比可以发现，模型预测的塑件最大Z向翘曲变形和缩痕深度与模拟分析结果之间的最大相对误差分别仅为3.7%和2.0%，均在工程计算允许的误差范围内，从而验证了所建立的多项式数学模型的有效性。塑件最大Z向翘曲变形和缩痕深度的二次多项式数学模型为

W_z=-244.50479+13.43483t_i+1.88174T_m+0.39662T_c+0.061072p-0.058250t_iT_m+

0.16630t_iT_c-0.0061150T_mT_c-2.17850t²_i-0.0031037T²_m+0.0076625T²_c （8-5）

S=3.34478+0.044533t_i-0.021428T_m-0.00893784T_c-0.014340p-0.00017500t_iT_m+0.000096667t_ip+0.0000030000T_mT_c+0.000035333T_mp+0.000017667T_cp+0.000037802T²_m-0.0000071765T²_c+0.000024467p² （8-6）

表8⁃9 关于塑件翘曲变形的ANOVA分析结果